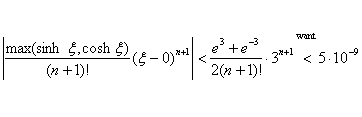|
W 4/1/09
|
HW due: Finish writing §12-3 #1-11 all; review
§12-4; write §12-4 #3, 6.
|
|
|
Th 4/2/09
|
HW due: Read the silly dialogue that follows; write
§12-4 #2, 4, 7.
Students may wonder aloud why it is worth developing a power series for f (x)
= 5e2x. Couldn’t we simply use a calculator and punch in e (approximately 2.718281828459) and
multiply it by itself the appropriate number of times?
Mr. Hansen’s response: What if the
exponent is not an integer? Raising e
to the 4th power is easy (square twice), but how can you raise e to the 3.9 power, for example? What
then? You’re going to need a power series.
Rebuttal from student who has studied
French: Au contraire! I will use my superior technology to raise any base
I wish to any exponent I wish, whether the exponent be positive or negative,
rational or irrational, real or imaginary.
Counter-rebuttal from Mr. Hansen:
But what do you think underlies that fancy technology of yours? Power series,
of course. Your calculator cannot raise an arbitrary base to an arbitrary
exponent by repeated multiplication. Repeated multiplication is a fine way to
define integer exponents, but in previous courses we have generalized to
allow the exponent to be any real number, as long as the base is positive. We
now need a way to compute these exponential functions!
Counter-counter-rebuttal from student:
OK, so you can compute e to some
power. Big deal. You still can’t raise arbitrary bases to arbitrary powers by
using power series.
Mr. Hansen (going in for the kill):
Au contraire! Remember that for any positive base b, bx can be
rewritten as ex ln b.
Student (filled with pride): Aha!
But you can’t compute ln b
accurately unless b is something
really simple like 1, e, or e2.
Mr. Hansen (smiling broadly): Oh,
you want to know about natural logs? No problem! There’s a power series to
compute those, too.
Student (starting to lose steam):
So, whatever, you can explain how the transcendental functions can be
computed on a scientific calculator. That brings us up to, what, 1976
technology?
Mr. Hansen: Actually, we can go far
beyond that with power series. Remember, one of the difficult problems of the
calculus is efficient quadrature. If the integral you are trying to compute
must be executed millions (or billions) of times as part of some slick new
software you are writing, the run time becomes an important consideration.
Rarely does the integrand have a closed-form antiderivative that would allow
you to compute an answer by FTC1. However, general quadrature using the
midpoint rule, the trapezoid rule, Simpson’s Rule, etc., may be too slow
and/or inaccurate for what you need. If your integrand is assembled from
functions whose power series are known, you may be able to write a power
series representation of the integrand and then antidifferentiate “term by
term” to get a good approximation for the original definite integral.
Student: Using what? FTC1 applied
to the terms of a polynomial?
Mr. Hansen: Precisely.
Student: Why is that better than
Simpson’s Rule? And does this method always work?
Mr. Hansen: If the Simpson’s Rule
implementation involves a number of expensive evaluations of transcendental functions,
then yes, power series might offer a faster, cheaper alternative. The other
caveat is that power series are valid only on a certain interval of convergence that must be determined for each problem
depending on the specifics.
Student: Sounds like a lot of work.
I think I’ll stick to Simpson’s Rule.
Mr. Hansen: Oh, I forgot to mention
one other big advantage of power series estimation. Often (especially in the
case of series whose signs alternate) it is relatively easy to compute an
error bound that depends on the number of terms. In other words, we can
compute in advance precisely how
many terms of the power series will be needed in order to guarantee accuracy
to within, say, 7 decimal places. With Simpson’s Rule, you may have a lot of
trial and error involved.
Student: Error bounds? Oh my! That
sounds like a lot of work.
Mr. Hansen, comfortingly: It is,
but we will take it a step at a time. Before long, you’ll know more than you
would ever have thought possible!
|
|
|
F 4/3/09
|
HW due: Review reading material as necessary; write
§12-5 #9, 12, 13, 14, 15-33 mo3. The first four of these should go very
quickly.
|
|
|
M 4/6/09
|
“Regurgitation”
Quiz (10 pts.) on the 8 standard
Taylor series (p. 616) and their intervals of convergence. The intervals of
convergence are the real line for all except the last three listed:
- The series for ln x converges only on (0, 2].
- The series for 1/(1 – x) converges only on (–1, 1).
- The series for arctan x converges only on [–1, 1].
HW due: Write §12-6 #1, 4, 7, 12, 13, 14, 15, 17,
19.
|
|
|
T 4/7/09
|
No additional textbook HW due. Continue working your
AP review problems, and use any leftover time to close up loose ends in your
previously assigned problems.
|
|
|
W 4/8/09
|
HW due: Re-read the green boxes on p. 630 and all of
§12-7; write §12-6 #22, 23, 25, 26. Note:
The root technique is not on the AP exam.
|
|
|
Th 4/9/09
|
HW due: Read the green box on p. 640; re-read all of
§12-8. There is no additional written assignment (other than reading notes,
of course, and your daily AP review log).
|
|
|
F 4/10/09
|
HW due: Write §12-7 #5-14 all, 25-30 all. The first
group (#5-14) are the most important, since they are the most similar to AP problems.
Solutions to the others are given below, but please refer to them only if you
get stuck. Try to do as much as you can before you give up!
25. Since this is a geometric series with common ratio r = 1/4 satisfying | r
| < 1, the series converges.
26. Much as in #25, this is a geometric series with r = 3/4, which satisfies | r
| < 1. The series converges.
27. The first term, in which n = 0,
is a term having value 1 with no effect on convergence. All other terms are
positive and are bounded above by 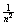 . Therefore, the series converges by comparison to a
p-series with p = 2. Or, if you prefer, you could say that the terms are all
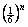bounded above by  , implying convergence by comparison to a geometric series
with r = 1/6.
Loose end for #27: If anyone doubts that the “nth term” (by which we mean the term indexed by n, or technically the (n + 1)st term of the series) is
bounded above by 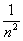 for all n > 0, then here is a sloppy but
valid proof:
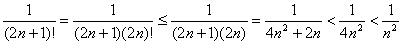
28. This is a convergent geometric series with r = –1/3, which satisfies | r
| < 1. Or, if you prefer, use AST instead.
29. Since  ,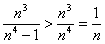
each term is bounded below by the corresponding term of the harmonic series.
Since the harmonic series diverges, the given series also diverges.
You could also use the integral test or the limit comparison
test. The limit comparison test is not covered in our textbook, nor is it
a requirement for the AP exam, but it is one of the most useful tests
available, since it can save you from the tedious inequality-crunching that
often accompanies other comparison tests.
30. Series diverges by the nth
term test. (The limit of the nth
term is not 0 as required for convergence.)
|
|
|
M 4/13/09
|
HW due: Write §12-7 #1, 2, 4, parts (a), (b), and
(c) of the problem stated below, and §12-8 #6. For §12-8 #6, you should read through
my work, which is also shown below, and adapt it when producing your own
writeup.
Problem: As you recall from much
earlier in the year,  .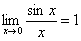
We can prove this either by the Squeeze Theorem or by L’Hôpital’s Rule.
However, Chapter 12 gives us yet a third way to do this.
(a) Write a power series for the quotient. No need to show steps; simply
write out the power series.
(b) Show that your power series converges for all x in a neighborhood of 0.
(c) To what value does your power series converge when x = 0?
Solution to §12-8 #6:
cosh 3 = 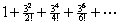 , where the terms are numbered according to the exponent.
“Real” term 1 has exponent 0, “real” term 2 has exponent 2, and so on. As n goes from 0 to 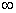 , the real term number (let us call it q) equals half the exponent, plus 1. In other words,  .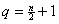
Let f (x) = cosh x and a = 0, thus giving Lagrange error term
of form  .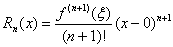
Since the derivatives of sinh x are
all either sinh x or cosh x, an upper bound for |Rn(x)| when 0 < x <
3 would be
 .
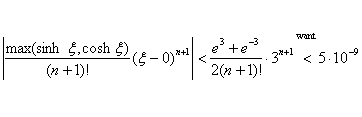The rationale for wanting the expression to be less than 5 · 10–9
is that 8 decimal places of precision will generally be ensured [see note
below] whenever the error is less than half of a unit in the 8th decimal
place, i.e., 0.5 · 10–8 or, equivalently, 5 · 10–9. The
easiest way to solve the inequality is to put the function
(e^3+e^(–3))/2/(X+1)!*3^(X+1)
into the Y1 function on your calculator. Then push 2nd TBLSET and
set TblStart=1,  Tbl=1, Auto, Auto. When you push 2nd TABLE, the values will
all be displayed for you. Scroll down to see the first value for which the Y1
expression is less than 5 · 10–9, namely 20.
[Note: Because there are certain
pathological cases where having error less than 5 · 10–9 does not
guarantee 8 digits of displayed accuracy, the AP exam does not pose questions
in this format. Instead, you will see a much more straightforward demand. For
example, you may be asked to compute the number of terms needed in the
partial sum in order to guarantee an error less than .001. That is a much
easier question, since you simply take whatever value is given to you and put
it on the right side of your “want” inequality.]
What does n = 20 mean? It does not mean 20 terms. What it means is
that 20 is the first n value that
ensures an error term less than 5 · 10–9 in absolute value. By our
rule above, the term number is found by  .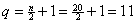
Final answer: The partial sum must have 11 terms.
If you wish, you can cross-check your work by computing partial sums as
follows:
Press MODE and select Seq instead of Func.
Press 2nd QUIT.
Press the Y= key.
Set nMin=0,
u(n)=u(n–1)+3^(2n)/(2n)! by using the 2nd function of 7 to
get u and the “ ” key to get n.
Set u(nMin)={1}.
Press 2nd QUIT.
Key in 2nd CATALOG D uparrow uparrow uparrow uparrow ENTER 3 ENTER to compute
cosh 3, namely 10.067662. (The actual value, which your calculator does not
show you, is 10.06766199578 . . .)
Key in u(1) ENTER to compute the 2nd partial sum, namely 5.5. This is, of
course, nowhere close to cosh 3.
Key in u(2) ENTER to compute the 3rd partial sum. Not much better!
Key in u(2)–cosh(3) ENTER to compute the error after the 3rd partial sum,
namely –1.192661996. No good!
Key in 2nd ENTRY and modify to get u(9)–cosh(3) ENTER. This gives the error
after the 10th partial sum, a very respectable –1.461 · 10–9. Now,
you might think that this would be enough to guarantee 8 places of accuracy,
but unfortunately here it does not. The issue is not whether the actual error
is less than 5 · 10–9, but rather whether the Lagrange error bound
can be guaranteed to be less than 5 · 10–9. The latter does not
occur until after the 11th partial sum, namely u(10).
Key in u(9) ENTER and notice that the 10th partial sum does not exactly equal
cosh(3). In fact, u(9), which is the 10th partial sum, displays as
10.06766199 to 8 places, while cosh(3) displays as 10.06766200 to 8 places.
The difference is caused by the small discrepancy in the 9th decimal place as
computed above.
Finally, key in u(10) ENTER to find the 11th partial sum. Now we have an
answer that agrees with cosh 3 to 8 decimal places. Whew!
|
|
|
T 4/14/09
|
Review day. No additional written HW is due, but you
should continue working review problems from your AP book.
|
|
|
W 4/15/09
|
Test (100
pts.) covering all material except for the Lagrange error bound in §12-8. This is the best day for the test, since no
HappyCal students have previous test conflicts on this day. We will have
another cumulative test including §12-8 next week.
|
|
|
Th 4/16/09
|
HW due: Continue working on AP review problems, and
as an exercise, rework your entire test from
yesterday under time pressure. You may omit problems that you are certain
you did correctly yesterday.
|
|
|
F 4/17/09
|
HW due: Work on AP review problems. In class, we
will work on §12.8.
|
|
|
M 4/20/09
|
Diversity Day (no class). Only A and B periods will
have a normal class today.
|
|
|
T 4/21/09
|
HW due: Write §12.8 #2-6 all, 11, 13, 14. Hint for #13: Draw a picture.
In class: Review.
|
|
|
W 4/22/09
|
Test (100 pts.)
in a “mini-AP” format. The first
half will be multiple-choice without calculator (10 questions in 20 minutes).
The second half will be free-response with calculator (2 multi-part questions
in 30 minutes). Time limits will be strictly enforced. All material from the
entire year is fair game. The key to the April
15 test is now available for your reference.
|
|
|
Th 4/23/09
|
HW due: Work on AP review problems.
|
|
|
F 4/24/09
|
HW due: Work on AP review problems. A quiz is also
likely.
|
|
|
M 4/27/09
|
No school (Phi Beta Kappa Day). If possible, I would
like to hold a full-length practice AP exam at 8:00 a.m. in the Mathplex.
Please hold the morning open for this valuable activity.
|
|
|
T 4/28/09
|
Review.
|
|
|
W 4/29/09
|
Another
“mini-AP” cumulative test (100 pts.), format reversed. In other words, the first half will be
multiple-choice with calculator (6 questions in 18 minutes). The second half will
be free-response without calculator (2 multi-part questions in 30 minutes).
Time limits will be strictly enforced. All material from the entire year is
fair game.
|
|
|
Th 4/30/09
|
Review.
|
|