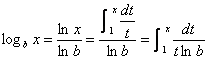|
M 11/3/08
|
HW due: Read §5-9; write §5-8 #6, §5-9 #2-38 even.
You may leave out a few when the process starts to become tedious, but be
sure to include #12 and #20 (to practice u-substitution)
and #26 (to practice limits).
|
|
|
T 11/4/08
|
HW due: Read §5-10; write §5-10 #3, 4, 7.
|
|
|
W 11/5/08
|
HW due: Read §5-11; write §5-11 #1, 2, 7-10 all, 15.
|
|
|
Th 11/6/08
|
HW due: Write §5-12 #R0 and as many of the other “R”
problems as you can. Answers are in the back of the book. If you need
additional challenge, try #C2, C5, and C6, all of which are examples of the
difficulty of problems that could appear on your test.
In class: Review for test.
|
|
|
F 11/7/08
|
No school.
|
|
|
M 11/10/08
|
Test #5
(100 points, cumulative through Chapter 5). In addition to the material represented by the “R” and “C” problems,
the “T” problems on pp. 246-247 are worth practicing. You are also
responsible for the exact statements of both versions of FTC, the proof that
FTC1 and FTC2 are equivalent, and the proof that the square root of 2 is
irrational. Those links are in the 10/31/08 calendar entry.
Here are some additional practice problems of the type that we did at the end
of class last Wednesday and again at the end of class on Thursday.
1. If dy/dx = 4 cos (e2x – x2), and if we know that y = –1.187 when x =
3.2, find y when x = 3.15.
2. I am thinking of a function H(x) whose derivative is known for all
real x. However, H itself is something of a mystery.
All I can remember is that H(2) =
3.5. Can you help me figure out what H(4)
equals?
3. A particle’s one-dimensional velocity along the x-axis is given by v(t) = 2et cos et.
At time t = 1 second, the
particle is 4.2 units to the right of the origin. Find the particle’s
position 1 second later.
Solutions (don’t peek until you have
tried to solve the problems on your own!):
1. Do you see that getting a function description for y is really nothing more than solving a differential equation
with initial condition (3.2, –1.187)? Now, finding a diffeq. solution for y in a simple formula (closed form) is
not something we can do, but that should not stop us. After all, we
learned—with great fanfare—that FTC2 guarantees that every continuous
function has an antiderivative, namely an accumulator function. The given
derivative of y is indeed
continuous. Therefore, let us form the proper accumulator function
(particular solution) as follows:
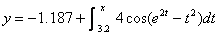
With some experience, you can write this function immediately, with only a
moment’s thought. The purpose of the constant –1.187 is to make sure that y has the proper value when x = 3.2. (The integral from 3.2 to 3.2
is 0.)
Pause for a moment to satisfy yourself that dy/dx is 4 cos (e2x – x2),
as required. (It works, by FTC2.)
All we have to do now is to plug x
= 3.15 into the particular solution for y.
By calc., the answer is approximately –1.188.
2. If you understood #1, you should be able to write the answer immediately:
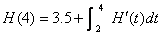
Presumably, since 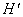 is known, finding
the above answer for H(4) should be
no trouble at all with a calculator. is known, finding
the above answer for H(4) should be
no trouble at all with a calculator.
3. Answer: 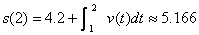 by calc. by calc.
This problem is somewhat unusual in that it can also be done without calc.
(via FTC1) as follows:
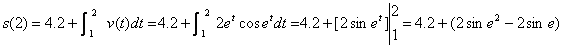
Take a moment to verify that the exact solution obtained by FTC1 matches the
first version.
|
|
|
T 11/11/08
|
HW due: Read §§6-2 and 6-3; write §6-3 #30-46 eoe
and yesterday’s test. (To save time, you may
omit question 11. However, be sure to do question 19 at the end, which was
omitted from the original test for reasons of time.)
Note: The abbreviation “eoe” is
found on the page of Mr. Hansen’s abbreviations.
|
|
|
W 11/12/08
|
HW due: Clean up any remaining lint from Monday’s
test; read §6-4; write §6-4 #7, 9, 11, 12, and prove the following theorem:
Change-of-Base Formula: If x > 0 and b > 1, then logb x = (ln x)/(ln b).
|
|
|
Th 11/13/08
|
HW due: Read §6-5; write §6-5 #3-30 mo3.
Challenge problem: Let f be
continuous and 1-to-1, and let b = f (a).
Prove that if (a, b) is an inflection point for function
f, then (b, a) is an inflection
point for f –1.
Ultra challenge: Find an “integral-type” definition for logb x, analogous to the definition 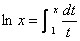 , without using the change-of-base formula. , without using the change-of-base formula.
Obviously, one simple way to make the definition would be to write 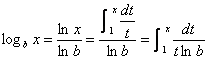 . .
Try to find a method that either skirts this obvious approach or uses this
definition to prove the validity of the change-of-base formula (without
resorting to circular reasoning).
|
|
|
F 11/14/08
|
HW due: Read §6-6; write §6-6 #5-12 all, 19, 20.
|
|
|
M 11/17/08
|
HW due: Read §§6-7 and 6-8; write §6-7 #4-60 eoe.
|
|
|
T 11/18/08
|
HW due: Read §6-9; write §6-8 #3-33 mo3.
Note 1: Normally, when we do
algebraic transformations leading to a final answer, the chain of equalities is
so obvious that there is no need to provide an explanation for each step.
However, with L’Hôpital’s Rule problems, there is always an abrupt “hop”
(sometimes more than one) where you apply the rule. I require that when
making the transition (i.e., applying L’Hôpital’s Rule), you show the
indeterminate form and the abbreviation “L’Hôp.” in the margin so that it is
clear what you are doing and why it is valid. For example, if a limit
expression has infinities in the numerator and the denominator, you would
write
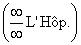
in the margin at the point of the transition to the new limit expression.
Note 2: Carry the word “lim” along
until the very end.
Note 3: If the final limit resolves
to infinity, you can conclude that the original limit was also DNE in the
sense of being infinite. However, on rare occasions, you may find that the
final limit is DNE by virtue of oscillation. In such a case, you cannot say
that the original limit was DNE. L’Hôpital’s Rule is inconclusive in such a situation. Your only choice would be to
restart the problem, using a different method of algebraic attack. Problems
of this type are rarely seen on the AP exam, but you should be aware of the
possibility.
|
|
|
W 11/19/08
|
HW due: Read §§7-1 and 7-2; write §6-8 #34, 36, §6-9
#81-90 all and as many of #1-89 as you can stand. (You may skip easy ones,
such as #69 and #75. Different students will have different ideas of which
problems are worthy of being written out.)
In class: We will orally go through #1-90 all, time permitting.
|
|
|
Th 11/20/08
|
HW due: Write §6-9 #21-89 all if you have not
already done so, and prove that
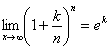 for any real
constant k. for any real
constant k.
This is a very useful lemma to have in our “bag of tricks.”
|
|
|
F 11/21/08
|
HW due: Read §7-3; write §7-2 #2, 5, 6, 8.
|
|
|
M 11/24/08
|
Test #6
(100 points, cumulative through §7-2).
The solution key to the previous test is now available at hwstore.org.
From the Department of Loose Ends:
I promised you an example of a limit that fails with L’Hôpital’s Rule.
Consider 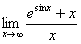 . Blindly applying L’Hôp. ( . Blindly applying L’Hôp. (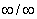 ) leads to ) leads to 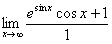 , ,
an expression that skips around, sometimes above 1, sometimes below 1, but
never settling down to a limit. The limit of the quotient of derivatives is
therefore DNE, and we have no
information about the original limit.
Applying non-L’Hôpital analysis is much more productive. We have
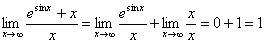 . .
The final two limits are found by inspection as follows: The first is 0,
since the numerator’s absolute value is bounded above by e, while the denominator’s value increases without bound. The
second is 1 for all nonzero x,
hence 1 in the limit since x > 0
can be assumed wlog.
|
|
|
T 11/25/08
|
HW due: Argue with your classmates, and prepare a
100% valid version (to the best of your ability) of yesterday’s test.
In class: Our guest speaker, Mr. Joe Morris (STA ’62) from the MITRE
Corporation will speak to us about the early history of computers.
|
|
|
W 11/26/08
|
No school (Thanksgiving break).
|
|