Geometry / Mr. Hansen
9/12/2008

Name: ___________KEY___________

Solution to Mini Practice Test 2 on Chapter 1

 

 

Scoring Guide: Statements and reasons must both be numbered. There are at least 7 statements and 7 reasons that are required. Givens can be crammed together into a single numbered item without penalty if you wish. Deduct 1 point for each missing statement and 1 point for each missing or incorrect reason, plus 1 point if the Q.E.D. or Halmos sign is missing at the end.

Take this question under time pressure (max. 10 minutes if this is the first time you have tried the problem, or about 6 minutes if you have seen it before).

With 15 points possible, grades are therefore as follows:

15 = 100% (A+)
14 = 93% (A)
13 = 87% (B+)
12 = 80% (B)
11 = 73% (C)
10 = 67% (D+)
9 = 60% (D)
<9 (F)

Deduct half a point for each minor formatting error. Examples include using lower case letters when upper case letters are required for the names of points, omitting an angle sign, forgetting to number a statement or reason, or misusing the degree symbol. If the same minor error (e.g., forgetting to number statements or reasons) is made throughout the proof, deduct only 1 point.

Correct:
Correct:
Incorrect:
Incorrect:

Deduct a full point if a reason is overly elaborate. For example, some students have a tendency to list the givens, state the conclusion, and give as a reason a long, involved explanation similar to this: “If the right angle is trisected, then each part is 30 degrees, and by adding two of these to the other given angle of 30 degrees, we have 90 degrees, which is a right angle.” Such a reason, though certainly mathematically valid, would be more appropriate in a paragraph proof, not a 2-column proof. The scoring for something like that would be 7 points out of 15, or 8 if the student included the Q.E.D. or Halmos sign at the end.

Order of the statements is somewhat flexible and need not precisely match the proof shown below. However, each statement that relies upon a previous statement must have the previous statement already in evidence. For example, you cannot say that  has a measure of 90 unless the fact that  is a right angle has previously been entered as a statement. Similarly, you cannot say that angles 1, 2, 3 each have a measure of 30 unless both the trisection and the fact that  has a measure of 90 have previously been entered as statements.

It is always acceptable to make notational additions to the diagram, such as adding angle names 1, 2, and 3. If you were to add a new ray, line, or line segment, however, you would need to use a dotted line and document the auxiliary ray, line, or line segment in the body of your proof.

 

 

1.

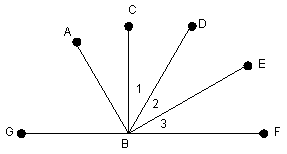
(15 points) Write a 2-column proof.

 

 

 

 

Given:  is a right angle

 

           

 

            trisect

 

Prove:  is a right angle

 

 

 

___________________________________________________________________

 

1.  is a right angle

| 1. Given

 

2.

| 2. Def. of rt.

 

3.  trisect

| 3. Given

 

4.

| 4. Def. of trisection

 

5.

| 5. Angle addition

 

6.

| 6. Subst. (2, 5)

 

7.

| 7. Alg. (4, 6)
|     [Or, you could say, “3 equal
|     quantities that add up to 90
|     must each be 30.”]

 

8.

| 8. Given

 

9.

| 9. Angle addition

 

10.

| 10. Subst. (7, 8, 9)

 

11.

| 11. Alg.

 

12.  is a right angle

| 12. Def. of rt.

 

(Q.E.D.)

 

 

 

 

 

Note: Not all of these steps are required. The versions given in class were significantly shorter. Specifically, it is acceptable to combine steps 4 through 7 into a single step 7 as shown below, provided that steps equivalent to steps 2 and 3 above have already been entered into evidence.

 

7.

| 7. Def. of trisection, alg.
|     [It is also acceptable simply to say,
|     “def. of trisection.”]

 

 

 

Making the change above would cut out 3 steps (steps 4, 5, and 6). Similarly, it is acceptable to cut out steps 9 and 10 by writing a single modified step 11 as follows:

 

11.

| 11. Subst. (7, 8) and angle addition

 

 

 

If you were to take advantage of both shortcuts, you would be left with only 7 required steps instead of the 12 steps shown in the proof.

 

 

 

There are no “bonus points” for having more than 7 steps. The maximum number of points in the proof would be 15, regardless of how many steps you write. The requirements can be summarized as follows:

 
  • All 3 givens must be written in the body of the proof. Merely doing this will earn you 6 of the 15 possible points.
  • No fact that depends on a given can be entered as a statement unless its associated given has already been entered. (For safety, therefore, some students simply make a practice of listing all the givens first. There is nothing wrong with doing this, but it could be argued that a proof is more readable if one brings in the givens only when needed, as shown in the 12-step proof above.)
  • Step 2 is required.
  • Steps 4-7 (which could be condensed to a single step 7 as described above) are required.
  • Steps 9-11 (which could be condensed to a single step 11 as described above) are required.
  • The conclusion (step 12) is required, and it must precisely match the original “Prove:” statement. It is not acceptable to end at step 11.
  • The Q.E.D. or Halmos sign at the end is required. If you failed in your proof, but you know that you failed, you can earn the Q.E.D. point by writing NR (for “not reasonable”) at the end.