|
F
5/1/09
|
HW due: Read §14.2.
|
|
|
M
5/4/09
|
HW due: Read §14.3; write §14.2 #1bdf, 3, 5ab, 9,
11, 1b*, 5a*, and 5b*. We did #1a in class last Friday.
For each problem, state locus 1, state locus 2, and then sketch and describe
all possible ways that the two loci can intersect to form a compound locus.
Examples are shown below, and more answers (assuming all loci to be in a
plane) are given in the back of the book. There is no credit for copying the
book’s answer unless you also provide the descriptions and the sketches.
* Also redo #1b, 5a, and 5b for loci in
space. The answers are given below, but of course the real work is in
providing the sketches.
1(b). Locus 1 is a sphere centered at A. Locus 2 is a sphere centered at B
but having a different radius. Compound locus is therefore  , a single point, or a circle. [Using pencil and paper
to show the intersection of two spheres is moderately difficult. However,
there is a brand-new SketchUp
model that shows this without requiring any software to be downloaded.
Can you guess who built the model?] , a single point, or a circle. [Using pencil and paper
to show the intersection of two spheres is moderately difficult. However,
there is a brand-new SketchUp
model that shows this without requiring any software to be downloaded.
Can you guess who built the model?]
5(a). Locus 1 is the union of a sphere and its interior (i.e., a solid ball).
Locus 2 is a line (given). Compound locus is therefore  , a single point, or a line segment. , a single point, or a line segment.
5(b). Locus 1 is the interior of a sphere. Locus 2 is a line (given).
Compound locus is therefore either  or a line segment
without its endpoints. [Note that it is not possible for the compound
locus to be a single point.] or a line segment
without its endpoints. [Note that it is not possible for the compound
locus to be a single point.]
|
|
|
T
5/5/09
|
HW due:
Read §14.4; write §14.3 #5-10 all. Most of this is a review of material we
covered last fall. The only new material is Theorem 131, which says that the
centroid is at a point 2/3 of the way
from any vertex to the midpoint of the opposite side.
The memory aids we learned last fall are restated below for your
recollection.
PBCC: In
any triangle, the perpendicular
bisectors coincide at the circumcenter.
ABIC: In
any triangle, the angle bisectors coincide at the incenter.
ALTO: In
any triangle, the altitudes
coincide at the orthocenter.
MCCG: In
any triangle, the medians
coincide at the centroid
(which is the center of gravity if the triangle is the
base of a very thin triangular prism of uniform density).
|
|
|
W
5/6/09
|
No additional HW due. Focus on bringing your
previously assigned problems up to date.
In class: Discussion of §14.4.
|
|
|
Th
5/7/09
|
HW due: Read §15.1; write §14.4 #4, 16a, 19. It is
suggested that you start tomorrow’s assignment as well, since today’s is
shorter than usual and tomorrow’s is longer than usual.
The assignment involves compass-and-straightedge constructions, which we did
last November and December. Therefore, students who have been with Mr. Hansen
since fall 2008 will find that these techniques are all a review of earlier
work we did. Students who joined in January may wish to view the step-by-step
instructions on the online animation pages listed in the 12/2/2008 calendar entry.
|
|
|
F
5/8/09
|
HW due: Read §15.2; write §15.1 #1, 2, 6, plus the
trig review problems 91-99 below.
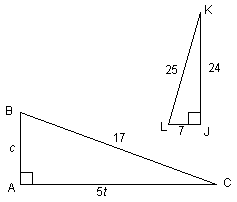
Compute each of the following:
91. sin 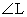
92. cos 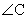
93. sin 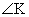
94. tan 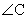
95. tan 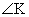
96. cos 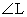
97. 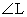 (to the nearest
degree, showing setup and answer in correct inverse-trig notation) (to the nearest
degree, showing setup and answer in correct inverse-trig notation)
98. 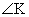 (to the nearest
degree, using same ground rules as in #97) (to the nearest
degree, using same ground rules as in #97)
99. AB to the nearest unit, if it is given that 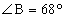
|
|
|
M
5/11/09
|
HW due: Read §15.3; write §15.2 #1, 2, 14; p. 684
#14, 16, 19, 22, 23, 24. If you cannot finish all of these, do most of them
and get the last few for tomorrow.
|
|
|
T
5/12/09
|
Review. There may also be a general HW check on any
assignment from the fourth quarter.
|
|
|
W
5/13/09
|
Review/catch-up day.
|
|
|
Th
5/14/09
|
7:00 a.m.:
Stotesbury participants and Sope will take Friday’s test in LJ-302.
In class: Construction portion of test, with remainder of period for review.
The test originally scheduled for today has been moved to tomorrow. You will
be required to construct the circumcircle for a
given triangle, as well as a line parallel to a given
line and passing through a given point not on that line. Both of these
are basic constructions that you can practice as many times as you wish by
using the provided animation links. Time limit (total for both constructions)
is 4 minutes and 30 seconds. Neatness counts. If you do not like the Office
Depot compasses in the class set, or if you do not like using the edge of a
piece of paper as a straightedge, please feel free to bring your own compass
and straightedge from home.
Note: For the second construction,
the parallel line, the animation contains one small error in step 4. The arc
mark must be shown in order to indicate that you have properly measured the
distance from the point above J to the point that is to the right of J.
|
|
|
F
5/15/09
|
Test (100
pts.), cumulative over all material for the entire year. Note that the date has been changed to today on
account of the Thursday-Friday schedule swap in effect this week.
|
|
|
M
5/18/09
|
Exam review. (“A” period class meets in Steuart 302
today and tomorrow.)
|
|
|
T
5/19/09
|
HW due: The three P’s (“plan, process, and product”)
for the problem of finding the exact circumcenter coordinates for a given
triangle ABC. Your personal coordinates for A, B, and C will be e-mailed to
you. This assignment will be scored as follows:
10 points for plan: As in
yesterday’s in-class exercise, you must describe the steps to be performed.
10 points for process: Show your
work in a neat, easy-to-follow manner. Use fractions, not decimals.
10 points for product: Your final
answer should be an ordered pair, (x,
y), giving the exact
coordinates of the circumcenter. Do not round your answer. Use fractions if
necessary. For example, do not write .6666667; write 2/3 instead. There is no
partial credit for a wrong answer, since you can (and should) cross-check
your work.
Bonus (2 points) for sketching the triangle, its circumcenter, and the
circumcircle.
In class: Exam review. (“A” period class meets again today in Steuart 302.)
|
|
|
W
5/20/09
|
Field Trip
to the National Cryptologic Museum, Fort Meade, MD. Bus leaves just after 8:00 a.m., so hurry back from
McDonald’s! We will be back on campus by 1:00 p.m. You are expected to attend
the second half of your F period class. Dress code is required for the field
trip unless you have purchased a tag from Ms. Spaulding.
HW due: Turn in the problem that was due yesterday. You can give this to me
at my lunch table (preferred), or you can give it to me on the bus.
Additional HW: Students not attending
the field trip are required to do the two additional problems listed below
(#2 and #3). Since you have 50 extra minutes, you can use what would
otherwise have been normal class time for that purpose if you wish. The
scavenger hunt has been dropped. The numbers that go in the blanks were
e-mailed to you at approximately 8:30 p.m. Tuesday. Problems 2 and 3 are due
at lunchtime at table 34. These are good problems, and everyone is
encouraged to do them as exam review. However, #2 and #3 are required only if
you are one of the students who are not attending the field trip.
2. A small bug sits on the sidewalk, ______ feet from the base of a tower.
The angle of elevation from the bug to the top of the tower is ______
degrees. Compute each of the following to 2 decimal places (i.e., to the
nearest 1/100 of a foot): (a) the height of the tower, and (b, c) the
straight-line distance from the bug to the top of the tower. For part (b),
use your answer to part (a) and the Pythagorean Theorem—no additional
trigonometry. For part (c), cross-check your answer to (b) by using trigonometry
but without utilizing your answer to part (a).
3. A right triangle has sides of ______ cm and ______ cm. The third side
(which could be either a hypotenuse or a leg—I will not say) can be found by
the Pythagorean Theorem. Find all possibilities for the third side (to the
nearest 0.1 cm) and the acute angles (to the nearest degree). Note: There are
two sets of possibilities.
|
|
|
Th
5/21/09
|
HW due:
Read the list of 36 final exam topics below, and make a handwritten list
of the topics on which you know you need more practice. Also, the
circumcenter assignment due Tuesday will be collected without penalty, as
well as #2 (bug problem) and #3 (angle possibilities problem). I will tell
you immediately whether your answers are correct.
Note: #2 and #3 are required for
students who were not on the field trip. If you were on the field trip, then
you are still encouraged to do #2 and #3, since they are good exam review
problems, but you are not required to do them.
Final Exam Topics
(compass-and-straightedge constructions are not on the final exam)
Simple radical form
Similarity and proportion
Altitude-on-hypotenuse theorems
Pythagorean Theorem and converse
Distance formula, diagonal of a solid
Triangle families (triples, 30-60-90, 45-45-90, equilateral)
Trigonometry
Radius-chord theorems
Chords congruent iff equidistant from center iff arcs congruent iff central
angles congruent
Circles: pi, circumference, area, arcs, and proration
Half SAD rules, corollary of cyclic quadrilaterals, corollary of external
tangent-tangent angle
Secant and tangent power theorems
Common tangent procedure
TTT
Inscribed and circumscribed figures
Walk-around problems
Area: triangle, trapezoid, parallelogram, kite, sector, segment, regular
polygons
Ratios of areas
Hero’s Formula
Lateral and total surface area: prism, pyramid, cylinder, cone, sphere
Volume: prism, cylinder, pyramid, cone, sphere
Graphing equations, especially linear equations (point-slope and
slope-intercept)
Systems of equations
Systems of inequalities
Equations of circles, incl. completing the square
Coordinate geometry proof
Coordinate geometry problems (2-D)
Coordinate geometry problems (3-D)
Locus and compound locus
PBCC, ABIC, MCCG, ALTO
Triangle inequality
Exterior angle inequality
Pythagorean Theorem test for acute/right/obtuse triangle
Hinge Theorem and converse
Basic triangle facts from first semester: BABS, ITT, external angle = sum of
rem. int., etc.
Pyramid facts: slant height, lateral edge, frustum
|
|
|
F
5/22/09
|
Last day of classes.
HW due (suggested): Make your final exam formula card for area and volume
formulas. Card dimensions are required to be 3 by 5 inches, no larger, no
smaller. If you do not have a card, a piece of paper of the proper size will
suffice.
You may put up to 6 formulas on your card. Only area and/or volume formulas
are allowed. You cannot put other theorems or the formulas for midpoint,
slope, or distance on your card. However, if you are clever, you can pack a
lot of information into your 6 formulas. For example, you could use these:

Do you see what this accomplishes? The first formula tells you not only the
TSA of a cone, but also the LSA (namely, 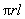 ) and the area of the circular base ( ) and the area of the circular base (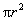 ). The second formula tells you the area of a circular
segment, and it also provides an example of proration to get the sector area,
and as a bonus, it uses Hero’s Formula for the triangle that must be
subtracted. The prism formula doubles as a cylinder formula (since for a
million-gon, a is approximately r, and p is approximately ). The second formula tells you the area of a circular
segment, and it also provides an example of proration to get the sector area,
and as a bonus, it uses Hero’s Formula for the triangle that must be
subtracted. The prism formula doubles as a cylinder formula (since for a
million-gon, a is approximately r, and p is approximately 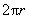 ), plus you have the regular polygon area formula, ), plus you have the regular polygon area formula, 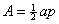 , built right in. The pyramid formula doubles as a cone
formula, since we know from the first formula that the circular base
satisfies , built right in. The pyramid formula doubles as a cone
formula, since we know from the first formula that the circular base
satisfies 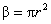 . Also, it is useful to know that a prism is like a
cylinder and that a pyramid is like a cone, since those facts can help you
keep the words “prism” and “pyramid” straight in your mind. Finally, the kite
formula is useful for rhombuses and squares as well, since every rhombus is a
kite, and every square is a kite. (And those are useful facts to know in
their own right, as you know.) . Also, it is useful to know that a prism is like a
cylinder and that a pyramid is like a cone, since those facts can help you
keep the words “prism” and “pyramid” straight in your mind. Finally, the kite
formula is useful for rhombuses and squares as well, since every rhombus is a
kite, and every square is a kite. (And those are useful facts to know in
their own right, as you know.)
Finally, the formulas that probably give students the most trouble are the
midpoint, slope, and distance formulas. You may have memorized the book’s
versions of these. However, if you understand the concept of “average”
(namely, add two things and divide by 2) and the concept of 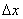 (namely, how much
has x changed, positive or
negative?), then you can memorize the simplified versions shown below. (namely, how much
has x changed, positive or
negative?), then you can memorize the simplified versions shown below.
|
|
|
|
Midpoint
Formula
|
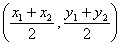
|
(xavg,
yavg)
|
|
|
|
Slope
Formula
|
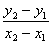
|
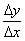
|
|
|
|
Distance
Formula
|
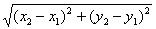
|
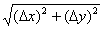
|
|
|
|
|
|

