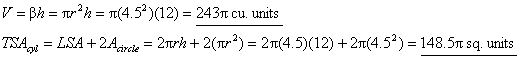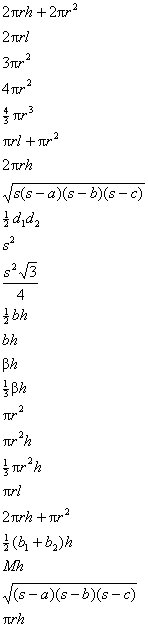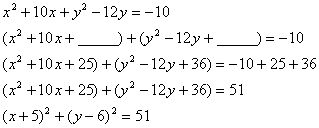Monthly Schedule

(Geometry, Periods A and F)

W 4/1/09

HW due: Read §12.4; write reading notes for §12.3 and §12.4; write §12.2 #10.

 

Th 4/2/09

HW due: Read your 13 lifetime learning items handout; write §12.3 #2, 3, 4, 7, 10, 11, 13. After making a diagram, be sure to include the three-stop process that we discussed for showing work: (1) formula, (2) plug-ins, (3) answer with units. Leave  as  (no approximations).

 

F 4/3/09

HW due: Read §12.5; write §12.4 #3, 4, 6, 9, 10, 12. Be sure to show your unplugged formulas clearly, and be sure to distinguish between square units and cubic units. Problem #10(a) is done as an example below, and you can feel free to copy it (if you add a diagram).

10.(a)

 

M 4/6/09

HW due: Read §12.6 and correct your §12.4 HW completely by comparing it against Sope’s excellent work; write §12.5 #1, 3, 4, 9, 13, 14, §12.6 #2, 4, 10, 11.

Extra credit (2 pts.): Show your work and estimate the volume and surface area of the earth.

 

T 4/7/09

HW due: Review problems, pp. 594-597 #1, 2, 6, 8, 10, 12, 18, 21. If time permits, also work on #3, 5, 11, and 13 for additional practice. (If time does not permit, then postpone #3, 5, 11, and 13 until tonight, when you are preparing for Wednesday’s test.)

 

W 4/8/09

Test on Chapter 12 (100 points). Bring all of your review problems to class and hand them in. The complete list is pp. 594-597 #1, 2, 3, 5, 6, 8, 10, 11, 12, 13, 18, 21. The even-numbered answers are now posted at hwstore.org, and some flash card suggestions are listed below. Happy studying!

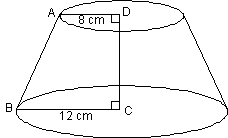
Suggestions for Making Flash Cards: If you know all of your formulas cold, then great. However, everyone could probably benefit by reviewing these. Remember, on the test you will be required to match formulas and their identifiers. When you practice, be sure to practice them in random order. Answers are posted at hwstore.org.

 

Th 4/9/09

HW due: Read §§13.1 and 13.2; write the frustum problem from yesterday’s test, which is reproduced below.

Note: On p. 612, you may omit the two-point form and the intercept form. We will discuss only the slope-intercept form (y = mx + b), the point-slope form (y – known yval = m(x – known xval)), and the general linear form (ax + dy = c). I do not use b in the general form, because the coefficient of y is not the same as the “b” in the slope-intercept form.

Compute the volume and total area of the frustum whose radii are shown. It is given that .

 

F 4/10/09

HW due: Read §13.3; write §13.1 #1, 4, 8, 9, 12, §13.2 #4, 6, 9, 13-16 all.

 

M 4/13/09

HW due: Read §13.4; write §13.3 #1, 3, 5, 9, 10, 14, and check hwstore.org to correct your answers and work that were due on Friday, 4/10.

 

T 4/14/09

HW due: Write §13.4 #1-7 all.

 

W 4/15/09

HW due: Review problems on pp. 644-646 #1-12 (all except 2, 3, 8), 15, 17, 21ab, 28. If you cannot finish all of these in one night, then do as many as you can, and do the rest on the night before Thursday’s test.

Also, be sure to do at least one 3-D plotting problem. I recommend #5abcd on p. 630. You may find the 3-D sketching handout to be helpful.

 

Th 4/16/09

Test (100 pts.) on all material through §13.4, plus one question on 3-D plotting. Important: Bring all of your review problems to be handed in. Even-numbered answers are available at hwstore.org.

 

F 4/17/09

HW due: Read §13.6 and the hints below; write §13.5 #5abcd, §13.6 #1, 2, 4, 5, 6. Hints are provided below for the §13.6 problems. If you do not utilize the hints, you may not be able to earn full points for the assignment.

1c. General form is . Here, (0, –2) plays the role of (h, k), and  plays the role of r. Plug in to get (x – 0)2 + (y + 2)2 = , which we simplify to x2 + (y + 2)2 = 12. Parts (a), (b), and (d) are very similar.

2. By inspection, determine what plays the role of (h, k) and what plays the role of r in each equation.  For example, h = k = 0 and r = 3 in part (a). Then plot the point (h, k) as the center and sketch a circle having radius r in each case.

4. Hint is already provided in the statement of the problem.

5a. Plug in 4 for x and 2 for y; see if the equation is a true equation. Show your formula and plug-ins.
  b. Plug in 3 for x and –2 for y. Then proceed exactly as in part (a).

6. You will have to invent terms for these.

 

M 4/20/09

Diversity Day (periods C through F only).

Period A: HW due today is to work at least a portion of the assignment due tomorrow. Bring your binder and show what you have done so far! After we talk about homework, we can have the finals of our Number/Spelling Bee and also run the brackets for a speed arithmetic tournament. The winner will face Sam Lo. from period F in a battle of the champions. Beware! Sam’s record is 25 seconds, which is hard to beat. Mr. Hansen’s record is 19 seconds, and the all-time STA student record, set by Sung Min Hong in 2008, is 21 seconds. If the weather is warm, we may also build a scale model of the solar system.

 

T 4/21/09

HW due: Read the “completing the square” procedure below and copy the example problem into your notes, line by line. Copy even the line that has the blanks! (The blanks remind you of the “holes” you will fill in on the following line.) Then try to adapt the example problem and the examples given in the textbook to write §13.6 #11, 12, 15.

HANDY 4-STEP GUIDE FOR COMPLETING THE SQUARE (see example below)
1. Look at the coefficient of x (namely, 10) or y (namely, –12).
2. Chop that in half. (That gives you 5 in the first case, or –6 in the second.)
3. Square your result from step 2. (That gives you 25 to add to the x expression, or 36 for the y expression.)
4. Remember that whatever you add to the left side of the equation must also be added to the right!





By inspection, the center is (–5, 6), and the radius is .

If you cannot perform the factoring in the final line of algebra, you need to see Mr. Hansen or Mr. Findler immediately for extra help. This is a basic skill that is taught in Algebra I, and you need to be able to do it.

 

W 4/22/09

HW due: Read §§9.9 and 9.10; write §9.9 #1, 4, 5, 7, 9, 10, 16.

 

Th 4/23/09

HW due: Write §9.10 #2-10 all, 15. In #15, please feel free to use “feet” to replace all occurrences of “dm” if you wish.

 

F 4/24/09

HW due:

The Great Pyramid near Giza, Egypt, before it eroded, was a regular square pyramid with base of side length 756 feet and height 480 feet. (These dimensions vary slightly depending on which reference you use, but we will use 756 and 480.) Refer to the diagram on p. 427 for #17. The Great Pyramid has AB=BC=CD=DA=756, PF=480. Your task is to calculate the four answers requested in #17 as if the pyramid were the Great Pyramid. Note: These answers can all be found on-line, and you are free to check in order to make sure that your answers are reasonable. However, you will receive no credit for the answers themselves. You will receive credit only for the work leading to reasonable answers. Use a calculator and the table on p. 424 for assistance. For full credit, a LARGE and reasonably neat diagram is required.

 

M 4/27/09

Phi Beta Kappa Day (no school).

 

T 4/28/09

HW due: Nothing additional, but be sure that Friday’s assignment is completely correct. Use the notes given in class to correct your answers to parts (a), (b), and (c). Part (d) can be found using the inverse tangent (tan–1), inverse sine (sin–1), or inverse cosine (cos–1) approach, much in the same way as we used the tan–1 function to estimate the answer to (c) to be 52 degrees.

Remember: “Inverse tangent” simply means that we have a tangent value, and we look it up in the table to see which angle comes closest to having that value for a tangent. (This is the inverse of what we usually do, which is to look up an angle on the leftmost column and then see what its sine, cosine or tangent equals.) In part (c), we found the tangent to be  Then, we needed to start a new line and write

.

In class: We will cover §14.1. Reading this in advance is a good idea but is not required.

 

W 4/29/09

HW due: Read §14.1; write §14.1 #2ab*, 3ab*, 4ab*, 5ab*, 9, 11, 14, plus p. 426 #6abc, 14, and the problem below.

Estimate the height h of the west tower of the National Cathedral if the angle of elevation measured at point W (wastebasket) is 65 degrees. Recall that the wastebasket (W) is 100 feet from the base (B) of the west tower. Please label your diagram with point T at the top of the tower, so that h = BT.

*For problems 2 through 5, do each problem twice, (a) as a locus of points in a plane and (b) as a locus of points in 3-dimensional space. Make a rough sketch and a description in each case.

In class: Review for test. Your anagram puzzle (4 words, something you need to know for Thursday) is

QUOTE FREE MALT SHOP COIN.

 

Th 4/30/09

Test through §14.1 (100 pts.). To help you with your studying, the homework solution handout for §14.1 is now available at hwstore.org. Please note, nothing quite as hard as #4b or #5b will be on the test.

 

 

Return to the Geometry Zone

Return to Mr. Hansen’s home page

Return to Mathematics Department home page

Return to St. Albans home page

Last updated: 01 May 2009