|
M
3/2/09
|
No school (snow day).
|
|
|
T
3/3/09
|
Test (100
pts.) on all of Chapter 10 and Class Discussions. Be sure to check hwstore.org
for answers and additional practice problems.
Questions: “Mr. Hansen, do I have to do all those review problems?
I mean, are you going to collect them?”
Answer to Question 1: Yes, you
have to do them.
Answer to Question 2: No, I do not
plan to collect them—unless you fail the test, in which case I may collect
them from a few students. Remember that the quarter ends in two weeks, and I
have to write detailed comments for every student. I need to be able to
report to your parents exactly how well you did (or did not) prepare yourself
for the test. There is no more revealing piece of information than how well a
student works when he thinks that his work product will not be “graded.”
You see, it’s like this: In a few years, you will probably be in college. Success
in college depends almost exclusively on the degree to which you take
responsibility for your own education. If you care, you will do well. If you
don’t care (i.e., if you do only the assignments that you know the professor
will collect or evaluate), you will not do very well, and you will not get
much out of the college experience except (possibly) a girlfriend and a piece
of paper called a diploma.
You and your family may invest more than a quarter of a million dollars in
your college education, or even more if you consider the money you do not
earn while you are attending college. That is a lot of money to spend for a
piece of paper, isn’t it? The only way it can possibly be worth the money is
if you take responsibility for improving your mind. My mission is to help you
in that quest, but there is only one person—you—who can do the job.
|
|
|
W
3/4/09
|
Whoops! I thought I had posted this, but according
to an e-mail I received at 10:08 p.m. on 3/3/2009, the assignment below was
not posted. When I double-checked the timestamp on the server, I realized
that, indeed, I had forgotten to copy the file to the server. Accordingly,
you may treat the reading assignment for today as optional, and you may treat
the proof as an extra-credit problem due on Friday, March 6.
HW due: Read §§11.1 and 11.2; write a 2-column proof for the problem below. Note: This problem comes from
yesterday’s A period test, but you are not to use proof by contradiction or
the secant-secant power theorem as was used on the test. Instead, use
auxiliary lines, HL, and CPCTC. You are allowed to assume that the curved
figure is a circle, but you are not allowed to assume that V is the center.
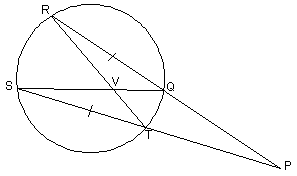
Given: QR = TS
Prove: PQ = PT
|
|
|
Th
3/5/09
|
HW due: Read §§11.3 and 11.4; write §11.1 #1-11 all,
§11.2 #1, 3, 4, 7, 8, 9, 14, 17, 25. Period A students may omit the ones we
did orally in class (namely §11.1 #1-10 and §11.2 #1), producing the
following reduced assignment: §11.1 #11 only, §11.2 #3, 4, 7, 8, 9, 14, 17,
25. Period F students need to add §11.2 #1c and 2 to the list.
|
|
|
F
3/6/09
|
HW due: Read §11.5; write §11.3 #1, 2, 3, 6, 7, 11,
13, 17, §11.4 #2, 3, 4, 5, 10.
|
|
|
M
3/9/09
|
Before school
(7:15 a.m.): COMMON TANGENT BOOT CAMP for everyone who had a failing score
(below 70) on the March 3 test.
Boot camp will be held in LJ-302, Mathplex North, with worksheets and lots of
direct instruction. A bonus of 3.25 points will be provided so that it is
worth your while. No, I cannot
force you to attend, but since there will be at least one common tangent
problem on tomorrow’s test, you need to be able to ace it. None of the
students who failed the March 3 test are experts on common tangents, and most
had a great deal of trouble with common tangents. If you feel you need more
practice on common tangents, you are welcome to attend even if you did not
fail the test, and you can earn the bonus. People who failed the test but do
not attend may expect their absence to be noted in their third quarter
comments.
HW due: Read §11.6; write §11.5 #1, 3, 5, 6, 9, 15, 20, and the problem
below.
Pentagon Problem: The Pentagon,
where Mr. Hansen worked for a number of years, is a large office building
whose outer wall forms a regular pentagon having apothem 634 ft. and side
length 921 ft. Compute the “footprint” (area) of the Pentagon in square feet
as well as in acres. Note: This
figure will not match the floor space figure published on various Internet
sites, nor will it match the area of the building proper, since there is a
large central courtyard as well as gaps between the five “rings” that make up
the building. Simply calculate the area of the large regular pentagon.
|
|
|
T
3/10/09
|
Test (100
pts.) on everything through §11.6.
Suggested review problems (be sure to check answers in back of book) are pp.
554-557 #1-13 odd, 19-33 odd.
Format of the test:
- A/S/N with Explanation (4 problems, 4 pts.
each; 1 pt. for correct answer, 3 pts. for explanation)
- Common Tangent Procedure (22 pts., same point
split as on the March 3 test)
- Multiple Choice (5 problems, 3 pts. each, no
partial credit)
- Area Calculation (5 problems, 6 pts. each; see
example below)
- Reverse Calculation (2 problems, 6 pts. each;
see example below)
- Proof (10 pts.)
- B0nu5 Probl3m (2 pts., taken from the 33 Numb3rs handout)
- Super Ultra Bonus (1 pt.): Whisper the word apothem as you hand in your
paper. If you pronounce it correctly, you will earn the super ultra bonus.
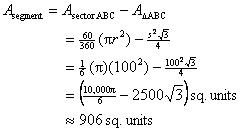
Example of
an area calculation problem:
Given circle C with radius as marked, compute the area of the shaded segment.
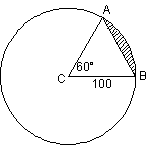
[Note that you must provide formulas,
plug-ins, and answer; numerical work alone will not earn full credit.]
Solution:
First, drop an altitude from A down to  , letting F be the foot of that altitude. Since , letting F be the foot of that altitude. Since  is equilateral, we
know is equilateral, we
know 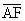 bisects bisects 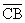 and creates two
30°-60°-90° triangles. Thus AF = and creates two
30°-60°-90° triangles. Thus AF = 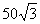 . .

[It is fine to leave your answer unsimplified.]
Alternate solution method, using the formula 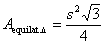 : :
Example of a “reverse” calculation
problem:
Given that the area of a regular hexagon is 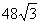 cm2,
compute the length of the apothem. cm2,
compute the length of the apothem.
Solution:
First, make a diagram in which the hexagon is subdivided into 6 equilateral
triangles, with the apothem of length a
creating two 30°-60°-90° triangles as shown below:
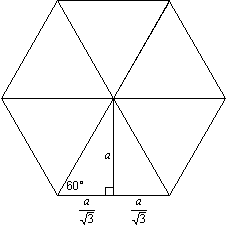
By properties of 30°-60°-90° triangles, each side is of length 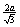 as shown. Therefore, as shown. Therefore,
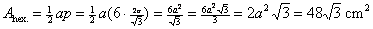
By algebra, 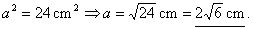
Another example:
Given that the area of parallelogram ABCD is 50 square meters, compute h.
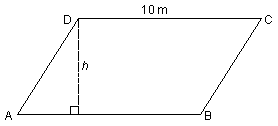
Solution:
Since A = bh = 10h = 50, algebra
gives h = 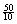 = 5 m. = 5 m.
Loose end from Monday’s class:
Problem #20 in §11.5 can be done without trigonometry, thanks to a suggestion
from an enterprising F period student. See, I knew I was not off base to assign it. Here is the trick:
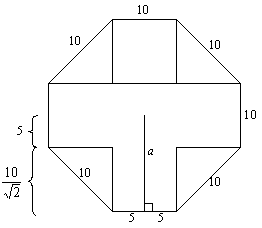
The apothem, a, can be broken down
into two parts as shown. The upper part is 5 by symmetry, since each side is
10. The lower part is 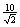 , which simplifies to , which simplifies to 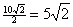 , since all of the triangles are 45°-45°-90°. Final answer: , since all of the triangles are 45°-45°-90°. Final answer:
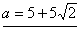 . .
|
|
|
W
3/11/09
|
HW due: Read §11.7. There is no written work (except
for your reading notes, as always), but be prepared for a general HW check.
Bring all assignments for the entire quarter, so that a random sampling can
be checked and/or collected for grading.
|
|
|
Th
3/12/09
|
HW due: Read §11.8; write §11.7 #1, 2, 7. “A” period
students may omit the written problems, since we covered them all in class.
Extra credit: The following
problems are fairly challenging. If you think you might want to try for
honors math someday, give them a try.
1.
Given: In diagram below, 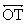 is tangent to circle
II at point T; is tangent to circle
II at point T;
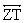 is tangent to circle
I at point T is tangent to circle
I at point T
Prove: 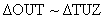
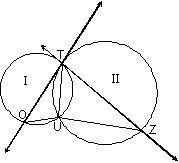
2.
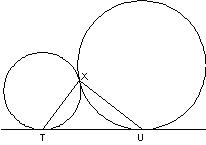
Given: Any two circles and a line as shown, with points of tangency at T, X,
and U
Prove: 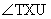 is right is right
|
|
|
F
3/13/09
|
Last day of third quarter. No additional HW is due
today, but we will have a Double Quiz
(10 + 10 pts.) on all material through the end of Chapter 11. One quiz will be
an angle-arc-segment puzzle, and one will be an area quiz possibly including
ratios and Hero’s Formula. Note that we are omitting Brahmagupta’s Formula.
|
|
|
Sat
3/14/09
|
Happy Pi Day and Einstein’s Birthday!
Note: Yesterday, Mr. Kelley’s
geometry class and Ms. Dunn’s two geometry classes performed the famous Buffon’s needle
experiment, using toothpicks instead of needles, and using lines spaced
exactly 1 toothpick length apart. The proportion of line crossings they
obtained was a good “Monte Carlo” estimate of the value of 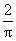 , as a result of geometric probability theory. , as a result of geometric probability theory.
Perhaps we will do this experiment someday. Or, if we are feeling
adventurous, we could try the slightly more bizarre Buffon’s noodle
experiment.
|
|
|
|
—Spring Break—
|
|
|
M
3/30/09
|
Classes resume. There is no HW over break. F period test
scores will be e-mailed to you sometime during the week of March 16. Third
quarter grades for all students will be e-mailed by approximately Wednesday,
3/25. In some cases you may also receive a preview copy of the comment that
will be sent to your parents.
|
|
|
T
3/31/09
|
HW due: Scan §12.3; write §12.1 #1, 4, 7, 9, §12.2
#1, 2, 4, 7, 8, 11.
|
|








