|
M
12/1/08
|
Classes resume.
HW due:
1. Get lots of sleep.
2. Correct your §6.3 assignment by visiting hwstore.org on Friday, Saturday,
or Sunday. Except for a few students in A period who took careful notes
during class last Tuesday (11/25), everyone still needs to do these
corrections. While you are at it, make sure that all your other second
quarter HW that can be corrected has been corrected, including the four
proofs (two from A period, two from F period) that were on Test #5 and Test
#6.
3. Review last Tuesday’s notes for the proof that the angles of any triangle
add up to 180 degrees. This is one of the components
of the course that you are expected to remember for a lifetime.
4. Bring your compass to class.
|
|
|
T
12/2/08
|
Construction
Quiz (10 pts.) based on a random
selection from the following techniques:
1. Bisect a segment.
2. Copy a segment
(easy).
3. Bisect an angle.
4. Copy an angle.
5. Drop a
perpendicular.
6. Erect a perpendicular.
7. Construct a
parallel.
Time will be strictly limited. Therefore, you must practice all the
techniques. Animations are available at http://www.mathopenref.com/tocs/constructionstoc.html.
You may also be asked to justify why
the constructions work. For example, #1 and #3 are based on kites or
rhombuses, #4 is based on SSS, #5 and #6 are variations on #1, and #7 uses #4
and the principle of corresponding angles.
A compass and a straightedge are required. You may use the edge of your
textbook without penalty if needed, but there will be a significant point
penalty for not having your compass.
|
|
|
W
12/3/08
|
HW due: Read §7.2; write §7.1 #1, 2, 4, 7, 9, 12.
Another quiz identical to yesterday’s (with randomly chosen constructions) is
possible.
|
|
|
Th
12/4/08
|
HW due: Read §7.3 and carefully review the proof of the
Midline Theorem (pp. 296-298); write §7.2 #3, 4, 5, and translate the Midline
Theorem proof into a 2-column format.
Hint: Regarding the short proofs
(#3, 4, and 5), one of them uses No Choice, and the other two use AAS. We now
accept AAS as a valid way to prove triangles congruent, but SSA remains
invalid in general.
|
|
|
F
12/5/08
|
HW due: Read §7.4; write §7.3 #1, 4, 5, 6, 10, 13,
14. Remember, for each question (including #14) you must provide explanations
and/or diagrams to justify your answers.
|
|
|
M
12/8/08
|
HW due: Write §7.4 #1-4, 10, 11, 13, 14, plus an
assortment (your choice) of review problems #1-21 on pp. 320-322. Solutions
to the §7.4 problems will be posted after class today to help you in your
studying for the test.
In class (A period): Go over HW, watch remainder of video.
In class (F period): Go over §7.3 and §7.4 HW.
If you missed the video last week, it will be shown beginning at 7:00 a.m. in
LJ-302 (Mathplex North). The first portion (the part seen by A period students
on Friday) will also be shown at 7:50 a.m. The video is also available here as a streaming video
file. Look for “Hunting the Hidden Dimension.”
The video is required, since questions from the video will be included on
tomorrow’s test.
|
|
|
T
12/9/08
|
Test #7
(100 points), cumulative through Chapter 7.
You can count on the following types of questions:
- Always, Sometimes, Never. The best way to
practice is to use Smokey or one of his cousins with the quad02.BA
program. Please come to Math Lab if you would like to practice.
- Algebra word problem(s). A good example is #18
on p. 322. Be sure to begin by using the word “Let.”
- Clock problem. I would like to retire these for
good, but that will not happen until the stragglers finally figure out
how to do them. For the rest of the students, these problems are like
free points to boost test scores.
- Crook problem: same comment.
- Indirect proof: same comment. The technique is
always the same, namely to show that by negating the conclusion (bwoc)
we are led to a contradiction. See these
examples of indirect proof.
- Constructions, chosen randomly from the 7
skills every student is supposed to know.
- Standard paragraph proof. I will flip a coin at
test time to determine whether you will do (1) the proof that two
parallel planes cut by a third plane have parallel lines of intersection
or (2) the proof that the angles of any triangle add up to 180 degrees.
You must provide a good diagram in either case.
- Problem(s) involving formulas. There are 3
formulas to memorize: the sum of angle measures of any n-gon = (n – 2)180 (p. 308), the number of diagonals of any convex n-gon = n(n – 3)/2 (p. 308),
and the sum of exterior angle measures for any n-gon = 360 (p. 308). A corollary of the last one is that
for an equiangular or regular n-gon,
each exterior angle has measure 360/n
(p. 315), but I cannot imagine that you would need to memorize that one
separately. Please note, there is a typographical error in your textbook
at the bottom of p. 308: The word convex
should be inserted immediately before the word polygon in the last line.
- Two-column proof. We have some additional theorems
we can use now, such as AAS, No Choice, and the Midline Theorem. A good
example problem is #3 on p. 320.
- Names of polygons: triangle, quadrilateral,
pentagon, hexagon, heptagon, octagon, nonagon, decagon. Beyond n = 10, we will simply say “n-gon.”
- Questions from the video. If you missed the
video, it is available here
as a streaming video file. Look for “Hunting the Hidden Dimension.”
|
|
|
W
12/10/08
|
HW due: Read §8.1; write the diagram, “given”
statement, and “prove” statement for the proof (reproduced below) that was on
yesterday’s test.
Given: ABCDEFGH is a regular octagon
Angles
BAF and AFE are right
Prove: AFGH is an isosceles trapezoid
|
|
|
Th
12/11/08
|
HW due: Write §8.1 #3-6 all, and finish your
portfolio of 7 construction techniques. Also, if you did not prove the problem assigned for
yesterday (as was my intention, though I forgot to say so), do that proof as
well.
Requirements for 7 construction techniques (bis. seg., copy seg., bis. angle,
copy angle, drop perp., erect perp., make ||): Write a “GIVEN” statement and
a “CONSTRUCT” statement for each one. Both statements should refer to
features of your diagrams by name and should list any properties. (For
example, for #2 your given is segment AB and line l, and your construction goal is a segment CD such that segment
CD is collinear with l and
congruent to segment AB.) Then do the construction, showing all of your work.
Non-star-worthy submissions will be rejected.
Note: Even those in A period who
had a large number of stars should proofread their work. Non-star-worthy
“GIVEN” or “CONSTRUCT” statements, for example, statements that do not refer
to features of the diagrams by name, will be rejected on the second review.
|
|
|
F
12/12/08
|
HW due: Read §8.2; write §8.1 #8, 11, 13, 22, §8.2
#2, 3, 6, 7. Also, your construction collection will be collected a second
time for a grade.
|
|
|
M
12/15/08
|
HW due: Read §8.3; write §8.2 #13, 14, plus the following
construction problems.
20. Given 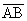 and and 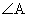 (i.e., an arbitrary
segment with an arbitrary adjacent angle), write the step-by-step
instructions for constructing a rhombus A'B'CD such that A'B' = AB and (i.e., an arbitrary
segment with an arbitrary adjacent angle), write the step-by-step
instructions for constructing a rhombus A'B'CD such that A'B' = AB and 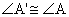 . Then do the construction. . Then do the construction.
21 (problem in honor of 12/12). Given 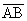 , write the step-by step instructions for constructing a
regular dodecagon A'B'CDEFGHIJKL such that A'B' = AB. This time, you do not
need to do the construction; simply write clear instructions. , write the step-by step instructions for constructing a
regular dodecagon A'B'CDEFGHIJKL such that A'B' = AB. This time, you do not
need to do the construction; simply write clear instructions.
Solutions to Friday’s HW have been posted at hwstore.org, and I would like
you to correct your answers if possible. Also, be sure to bring in your
construction portfolio again. So far, only 2 students’ collections have been
fully certified.
|
|
|
T
12/16/08
|
HW due: Read §8.4; write §8.3 #3, 6, 8, 10, 13.
|
|
|
W
12/17/08
|
HW due: Read §8.5; write §8.4 #1, 3, 6, 7, 9, 20,
plus the question below.
25. For as long as Mr. Hansen can remember, there has always been a question
on the midterm exam resembling #20 on p. 350. Explain why there is no credit provided for a student who
lets x denote the unknown distance
and sets up the proportion
12/5.5 = 3/x.
|
|
|
Th
12/18/08
|
HW due: Write §8.5 #3, 4, 7, 8, 14, 19a, plus the
question below.
31. Explain why the diagram in #3 is impossible.
|
|
|
F 12/19/08
|
Announcement:
Period A class will meet in Steuart 302 today.
HW due: Visit the exam study tips page
and write out all the answers to the study guide (pp. 1-3 of the practice
midterm exam posted on that page).
Note: You are exempt from this
assignment if Mr. Hansen checks you off his roster Thursday night at the west
exit of the Cathedral as you and your family depart from the Lessons and
Carols service. Mr. Hansen will stand there at the end of the service,
chatting with former students. Be sure you have been checked off the list,
even if you sing in the chorale or play in the orchestra!
|
|