|
M
11/3/08
|
HW due: Read §5.5; write §5.4 #6-10 all, 14. Then, on
Sunday evening, go to hwstore.org and correct your §5.2 and §5.3 HW to 100%,
using a different color. If you did not leave enough space in the margins to
accommodate corrections or improved diagrams, use off-page connectors so that
I can find your original and corrected versions easily.
(An off-page connector is a box that says, for example, “See corr. for #7 on
p. 4.”)
|
|
|
T
11/4/08
|
HW due: Read §5.6; write §5.5 #1, 3, 4, 7, 10, 11,
14.
Geometry grade reports for the first quarter will be e-mailed to you sometime
today. Until then, please do not ask me individually to look up or compute
your grade, since that will only slow down the process for everyone.
|
|
|
W
11/5/08
|
HW due: Write §5.5 #15, 17, 18, 19, 23, 26, 28, 29.
Treat these as review problems for the test. If you cannot do all of these,
make sure you at least do #29.
|
|
|
Th
11/6/08
|
Test #5
(100 points, cumulative through §5.5).
The following types of problems are guaranteed to be included on the test:
- Always/sometimes/never problems, some of them
harder than §5.4 #8 (previously assigned). For a more representative
set, see #19 on p. 266.
- Algebra word problem(s) similar to §5.5 #28,
though with easier numbers.
- Logic problem involving implications and/or
Venn diagrams.
- Clock problem.
- Proof by contradiction.
- Standard 2-column direct proof.
- Crook problem. It is easy to make up practice
problems for yourself. If you get tired of doing that, then try #25 on
p. 267. If you get stuck on #25 and need a hint, read the calendar entry for 11/9/2007.
- Problem(s) involving slopes, medians,
altitudes, opposite reciprocal slopes, and midpoints. One of the review
problems assigned for yesterday (§5.5 #26) has all of these features in
a single problem.
You should also be able to fill in any missing steps in the proof that the square root of 2 is irrational.
The following additional review problems on pp. 264-267 are recommended:
#1-11 all, 16, 18, 19, 21, 25, 26. Read and think about all of them, and
write up the ones that are worthy of spending the time for a writeup.
|
|
|
F
11/7/08
|
No school.
|
|
|
M
11/10/08
|
HW due: Read §5.7; write §5.6 #1, 3, 4*, plus your
choice of the A period proof or the F period proof from last Thursday’s test. Since
the proof will probably be collected, you should do a good job. Neatness
counts. If you have poor handwriting, then please use a typewriter or ask a
parent to transcribe the proof for you. The 3-day weekend should give you ample
time to write out a good, clean proof.
* Problem #4 need not be written out. If you prepare #4 orally, that is good
enough. You may wish to make light pencil marks in your textbook.
Note: For all students who did
poorly on last Thursday’s test, I may also be collecting your review problems
(assignment due Wednesday, 11/5). The reason is that if midquarter comments
need to be sent home, I need to know whether your low grade was caused by a
lack of preparation or by a test that was simply too difficult.
|
|
|
T
11/11/08
|
HW due: Read §6.1; write §5.7 #2, 6, 8, 10, 11, 13,
plus the other proof (either the A period proof
or the F period proof) that you did not do for
yesterday. The same rules regarding neatness and completeness apply. You may
wish to do the proof first in order to make sure that you finish it.
Hint: Now that you know additional ways of proving quadrilaterals to
be special figures, the proofs from the tests can be shortened somewhat. For
example, you no longer have to prove that a figure has four right angles in
order to prove that it is a rectangle. It suffices to show that you have a
parallelogram with one right angle.
|
|
|
W 11/12/08
|
HW due: Write #23 on p. 267 and the word problem
given below, and organize your
homework binder so that all assignments from the second quarter are in
order by date. (Reverse order by date is also acceptable, if that is what you
prefer.) First quarter homework may be recycled if you wish. I will be
checking for the assignments listed below.
Due 11/3: Corrections (in a different color) for §5.2 #2, 3, 4, 5, 6, 8, §5.3
#3, 4, 5, 7, 10, 27.
Due 11/3: §5.4 #6-10 all, 14; reading notes for §5.5.
Due 11/4: §5.5 #1, 3, 4, 7, 10, 11, 14; reading notes for §5.6.
Due 11/5: §5.5 #15, 17, 18, 19, 23, 26, 28, 29.
Due 11/6 (optional): selection from pp. 264-267 #1-11 all, 16, 18, 19, 21,
25, 26.
Due 11/10: §5.6 #1, 3, 4 (oral), plus A period
proof or F period proof; reading notes
for §5.7.
Due 11/11: §5.7 #2, 6, 8, 10, 11, 13, plus F
period proof or A period proof; reading
notes for §6.1.
Due 11/12: p. 267 #23 and the word problem below (with the blank replaced by
your personal value).
Word problem:
An angle is ________ degrees smaller than half its supplement. Find the
complement of the unknown angle. Give your answer in degrees and minutes.
In order to complete this problem, you will need to fill in the blank with
the following value depending on your name:
Abbott=4, Alex=5, Chris B.=7, Chris J.=8, Danny=10, Doug=11, Dylan=13, Eric
S.=14, Erik B.=16, Gabe=17, Greg=19, Guy=20, Hank=22, Ivan=23, Jacob=25,
Kealan=26, Kieran=28, Miles J.=29, Miles P.=31, Peter=32, Ryan=34, Sam
Le.=35, Sam Lo.=37, Sope=38, William=41.
|
|
|
Th
11/13/08
|
No additional HW due (because of Wednesday’s
required evening assembly).
However, I do expect you to have your Mr.
Hansen’s Quadrilateral Shop worksheet essentially complete so that we can
discuss it in class today. The other assignments that were due yesterday
(11/12) may be scanned and/or collected.
|
|
|
F
11/14/08
|
HW due: Finish up your Mr. Hansen’s Quadrilateral Shop worksheet,
and write pp. 264-267 #1 (sketches required for each), 2, 3, 7, 11, 19, 25.
Note: Since we went over #23 on p.
267 yesterday, you are also expected to have a clean version of that proof in
your binder. Please visit hwstore.org
if you need help. Do not copy the version that is posted there (unless you
literally have no idea how to start), but use it as a guide to help you
correct your version and learn from your mistakes.
|
|
|
M
11/17/08
|
HW due:
1. See §5.7 #8 (from the assignment due Tuesday, 11/11) in the HW store.
Correct your version as necessary, using a different color.
2. Reread §6.1 (already assigned for 11/11) and do Sample Problem 1 on p.
272. Copy the diagram (trace it if necessary) and practice making
3-dimensional drawings of this type. Then answer the questions using the
format shown below. Observe how it is not acceptable simply to write the
answer. You must write the setup of the question (and think about what the
question is asking) and then give the answer, boxed or circled.
Examples of correct answer format:
a) 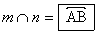
b) A, B, V det. plane 
3. Write §6.1 #2 on p. 273, using the same format.
4. Learn from your mistakes by correcting the back side of the Quadrilateral Shop handout with the
following answer key:
|
|
|
|
Quad.
|
A*
|
S
|
S
|
S
|
S
|
S
|
S
|
S
|
S
|
S
|
S
|
S
|
|
|
|
Convex Quad.
|
A
|
A*
|
S
|
S
|
S
|
S
|
S
|
S
|
S
|
S
|
S
|
S
|
|
|
|
Parallel-O-Gram
|
A
|
A
|
S
|
S
|
S
|
S
|
A*
|
S
|
S
|
A*
|
A*
|
S
|
|
|
|
Rectangle
|
A
|
A
|
A
|
A*
|
S
|
A
|
A
|
S
|
S
|
A
|
A
|
S
|
|
|
|
Rhombus
|
A
|
A
|
S
|
S
|
A
|
S
|
A
|
A
|
A*
|
A
|
A
|
A*
|
|
|
|
Kite
|
A
|
S
|
S
|
S
|
A*
|
S
|
S
|
A*
|
S
|
S
|
S
|
S
|
|
|
|
Square
|
A
|
A
|
A
|
A
|
A
|
A
|
A
|
A
|
A
|
A
|
A
|
A
|
|
|
|
Trap.
|
A
|
A
|
S
|
N
|
N
|
S
|
N
|
N
|
N
|
N
|
N
|
N
|
|
|
|
Isosc. Trap.
|
A
|
A
|
A
|
N
|
N
|
A
|
N
|
N
|
N
|
N
|
N
|
N
|
|
|
T
11/18/08
|
Announcement:
Period A will meet in Steuart 302 this morning (Tuesday).
HW due: Correct yesterday’s HW using Sope’s paper (as posted in the HW
store). Then read §6.2 and write §6.1 #4, 8, 11, 13, 14.
|
|
|
W
11/19/08
|
HW due: Correct yesterday’s §6.1 HW using the
posting in the HW store. Then read §6.3 and write §6.2 #1, 2, 3, 4, 6, 11.
|
|
|
Th
11/20/08
|
Test #6.
Sections 6.1 and 6.2 will be covered (check hwstore.org later Wednesday
evening for helpful solutions), but 6.3 will not be covered.
|
|
|
F
11/21/08
|
HW due: Work both
the A period proof and the F period proof from yesterday’s test. Provide a
full 2-column proof for each. Also explain in each case why the figure in
question (ABCD for A period, triangle ABT for F period) must be a plane
figure.
|
|
|
M
11/24/08
|
HW due:
1. Correct Friday’s homework by visiting hwstore.org. Use a different color of
pencil (or a colored pen) when you make your corrections. Note that there are
many correct proofs possible; all you need to do is alter your versions to
make them valid. It is not necessary to match the solution key precisely.
2. Practice copying the diagram on p. 283 so that you can easily sketch two
parallel planes cut by a third.
3. Memorize the statement of Theorem 49 and its proof. Practice writing the
theorem and a paragraph proof similar to the one given on p. 283.
4. At the beginning of the year, I announced that you would need to purchase
a compass at some point. That time has arrived. Please bring a compass to
class today and for approximately the next two weeks.
5 (optional). Bring a straightedge if you have one. In a pinch, you can use
the edge of your textbook without penalty.
A decent compass will cost you about $2 at Wal-Mart or Office Depot. Less
expensive ones are available, but avoid the $1.19 cheapies that work for only
a day or two. (They are also dangerous to carry around.) Many supermarkets
and drugstores sell compasses. Office Depot sells a great compass for $7 made
by Staedtler, model 9582. The Staedtler 9582 has a “halfpipe” design that
lets you carry it safely in your shirt pocket or pencil case.
In class: Quiz on Theorem 49 (10
points). I will say, “Go,” and you will have exactly 10 minutes to make the
sketch and write something similar to the following, without notes:
Given parallel planes m and n, cut by a third plane s, we wish to show that the lines of
intersection are parallel. Since the lines of intersection both lie in s, they are coplanar. Since the lines
of intersection also lie in m and n, respectively, the two lines can
never cross, since m || n. Therefore, by def. of || lines, the
lines of intersection are parallel. (Q.E.D.)
I obtained the figure of 10 minutes by timing myself as I wrote out the
sketch, theorem, and proof. It took me 2 minutes and 30 seconds, but I
multiplied by 4 to give you a good opportunity to succeed. With practice, you
can surely do these tasks in 10 minutes. There will be a bonus point if you
show the hidden lines properly as dashed or dotted lines.
|
|
|
T
11/25/08
|
HW due: Read §7.1 and this animated circumcenter
construction page; write §6.3 #10, 11.
|
|
|
W
11/26/08
|
No school (Thanksgiving break).
|
|