|
W
10/1/08
|
HW due: Read §§3.1 and 3.2; write §3.1 #1, 2.
|
|
|
Th
10/2/08
|
HW due: Read §3.3 (mostly review) and §3.4; write
§3.2 #1, 2, 4, §3.3 #2-7 all, 11.
You may copy my solution of §3.3 #4 as an example. It is now available in the
HW store. (Note: Normally, HW copying is forbidden, actually an honor
offense, but I am explicitly granting you permission to copy this problem if
you wish.)
|
|
|
F
10/3/08
|
ANNOUNCEMENT:
“A” period will meet in SB-302 today (top floor, Steuart Building).
HW due: Read §3.5; write §3.4 #1, 4, 6, 8, 10, 13, 15. Students who watched
last night’s vice presidential debate (and who bring good notes) can do a
reduced set of problems without penalty.
Now offered in the HW store is a
writeup of the “The X” (the proof we did in class yesterday).
|
|
|
M 10/6/08
|
HW due: Explore modd.net. Especially be sure to read
Mr. Hansen’s three rules and Mr. Hansen’s policies concerning absences. Both
links are available on the main modd.net page. Also check out a few of the
“Fun Links” underneath.
Important: This is not a weekend
without homework. This is a chance (and I expect you to utilize it) to get
caught up on problems that you may not have had time to get to last week.
Also, if you find any policies that are unfair or, in your opinion, should be
changed, please write them down and let me know.
There are basically four things we have learned this year that I would like
you to have really learned, i.e., committed to your long-term memory:
- What is math?
- What are inductive and deductive reasoning?
Which do you prefer most of the time?
- Remember “The X” (forward and backward chaining
example).
- Remember the bamboo.
“The X” is now available in
the HW store, and I would be most
grateful if you would read it over and learn from it. Remember, when we did
it in class on Thursday, I asked you not to take notes. However, you should
spend some time and look it over now to make sure you understand it.
|
|
|
T
10/7/08
|
HW due: Read §3.6 and this
link to the Encyclopædia Britannica; write §3.4 #10, 15 (neatly redone,
for handing in), §3.5 #4, 7, 9.
Hints (consult only if you get
stuck in §3.5):
For #4, use triangles BCD and EDC.
For #7, use triangles OPR and SRP.
For #9, use triangles AWY and XWZ.
|
|
|
W
10/8/08
|
HW due: Read §3.7; write §3.6 #2, 4, 6, 13, §3.7 #2,
9, 10.
Note: In our class, we will often
use the abbreviation ITT (Isosceles Triangle Theorem) for both Pons Asinorum
and its converse, the theorems that your book calls Theorems 20 and 21. If
you wish, you may also use the little symbols with the implication arrow (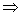 ) as reasons in proofs. ) as reasons in proofs.
Additional recommended reading: Please
see the HW store for versions of the
Pons Asinorum (a.k.a. ITT) from both A and F period.
|
|
|
Th
10/9/08
|
HW due: Read §3.8; write §3.8 #1-9 odd. If you get
stuck on #3, please see the hint below.
Hint for #3 (read only if you are
stuck): Use as one of your steps the construction of a dotted segment
from O to X. For your “reason” you can say, “Two points determine a line.”
|
|
|
F
10/10/08
|
No school (faculty professional day).
|
|
|
M
10/13/08
|
No school (holiday).
|
|
|
T
10/14/08
|
HW due: Do a large selection of review problems from
the Chapter 3 review (pp. 162-164) and the Cumulative Review (pp. 165-167).
This will be a double-credit HW scan. I will be able to tell at a glance
whether you took the assignment seriously. This is your preparation for the
test, and you might as well practice showing problems legibly, to test
standards, under time pressure.
Would you show up for a football, soccer, lacrosse, or track competition
having not practiced? Of course not. Would you play a piano recital or
perform on guitar for your friends having not practiced? Of course not.
Practice is the only way to learn mathematics. It’s not a bad idea to do some
of the problems more than once, in fact, since if you spend a lot of time
figuring out what you are doing, you still need to practice a second time for
speed and proficiency.
In class: Review. Some of the solutions are now posted in the HW store.
|
|
|
W
10/15/08
|
Test #3. Like all our tests, this one is cumulative. Chapter
3 will be the focus of the test, but all material from the entire year is
fair game. This is one reason that you will want to do the Cumulative Review
problems. Some of the review problem solutions from pp. 162-167 are now
posted in the HW store.
One topic area that is missing, however, is logic problems. Another is
PBCC/MCCG/ALTO/ABIC. Here are a couple of quick review problems to help you:
1.(a) Given: No fleems are sneepy. Some glams are fleems, but some are not.
Are there any glams that are neither fleems nor sneepy?
(b) If we are also given in part (a) that there are no sneepy
glams, how does that change the answer to the question that was posed?
2(a) Sketch an obtuse triangle HAN and indicate how to find its centroid and
orthocenter. Label these as C and O, respectively.
(b) What point is found at the intersection of the perpendicular
bisectors of 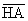 and and 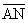 ? Circle one: incenter orthocenter circumcenter centroid 9-point
center ? Circle one: incenter orthocenter circumcenter centroid 9-point
center
(c) (BONUS) What point is found midway between the orthocenter
and circumcenter? Note: This question is quite advanced and is not covered
in your textbook. If this question were to occur on the test, it would be
only as a bonus.
The solutions are in the HW store.
|
|
|
Th
10/16/08
|
HW due: Read §4.1; write this
proof. Letters always refer to the closest corner or crossing.
|
|
|
F
10/17/08
|
Optional
Re-Test at 7:15 a.m. in Mathplex North. If you were unhappy with your score (which will, hopefully, be
e-mailed to you by late Thursday evening), you may take a re-test. The two
scores will then be averaged together if they help you. If the re-test score
does not help you, it will be ignored.
Note: In order to help you study, I
have posted some blank tests and answers in the HW store.
HW due: Read §4.2; write §4.1 #1,
3, 4. In the reading, there is a lot of good information, including the word
“overdetermined” and the explanation on p. 178 of how to make drawings when
very little is specified. Please read carefully.
|
|
|
M
10/20/08
|
HW due: Read §4.3; write §4.1 #2, 5, 6, 9, §4.2 #1-8
all. This looks like a lot of problems, but trust me, the §4.2 problems are
very quick. Please click here for two examples, which you are permitted
to copy if you wish.
A big “F period welcome” goes to Mac, who is planning to return to class
today! Also note, the F period class will be taught today by Dr. Betsy
Bennett, a retired master teacher who taught at STA for many years and at
Maret before that. You will, I trust, be on your best behavior for her.
|
|
|
T
10/21/08
|
HW due: Read §4.4; write §4.3 #1, 3, 5, 8, 9, 11,
12. Note for #8: The word “integral” in this context means “consisting of
integers.”
Important announcement: Period A
will meet in Steuart 302 today. (Period F will be in Mathplex North as
usual.)
|
|
|
W
10/22/08
|
HW due: Read §4.5; write §4.4 #2, 4, 5, 12, 16, and
the PBT Mastery Quiz. Perfection
is not expected, especially on the first try. However, try your best each
time to locate the “tower” that perpendicularly bisects the segment
connecting the “base anchors.”
Here is a paragraph proof of #1 on p.187 to get you warmed up:
Add auxiliary segments OA and OB. Since these radii are congruent, O is
equidistant from A and B. However, M is also equidistant from A and B. Since
points O and M determine a line, segment OM perpendicularly bisects segment
AB. (Q.E.D.)
The two-column version of this proof is available at hwstore.org. The proof
would be fairly long and tedious with congruent triangle techniques, but with
PBT it takes only about 7 steps (6 if you put both of the auxiliary line
constructions in the same step).
|
|
|
Th
10/23/08
|
HW due (reduced set in order to allow you to attend
the Choral Festival at the Cathedral): Write §4.4 #10, 20, and make a puzzle
for a friend to solve. Your puzzle need not be as difficult as the one we did in class on Wednesday, but
try to make it somewhat challenging. Your friend should write (a) his name,
(b) his list of all the perpendicular bisectors in your diagram, and (c) his
list of all the pairs of segments that can be proved to be congruent.
Auxiliary segments, if any, should be shown with dashed lines.
Bring your friend’s attempt at solving your puzzle to class. You and your
friend can work on your puzzle during the down time at the Cathedral.
Hint: Although #20 is in the “C”
set, it is a very short proof if you know what you are doing. Take full
advantage of the PBT.
|
|
|
F
10/24/08
|
HW due: Read §4.6; write §4.5 #2, 4, §4.6 #1-6 all,
10, 11.
In class: Review for test.
|
|
|
M
10/27/08
|
Test #4. You can prepare a practice test for yourself by
assembling the following ingredients:
- Half a dozen “always/sometimes/never” problems
- A clock problem (e.g., find the angle between
the clock hands at 7:29 p.m.
- At least two algebra problems, one of which will
be a word problem
- A logic problem involving implications or Venn
diagrams
- Three proofs, one of which may be impossible
(i.e., overdetermined or underdetermined*)
- A PBT puzzle: Identify all the perpendicular
bisectors and find all the congruent segments
* “Overdetermined” means that the diagram involves too many givens. In other
words, the givens could not possibly all be true at the same time, and if you
were to try to construct the diagram using Geometer’s Sketchpad, you would
fail. “Underdetermined” means that there are not enough givens; in other
words, the diagram could be adjusted in such a way that all the givens remain
true but the conclusion would be false.
Many of the problems will be similar to the Chapter 4 review problems on pp.
206-209. Check back on Saturday afternoon, since I will be posting some of
the solutions on hwstore.org.
Don’t forget! The final thing you need to do to prepare for the test is to
get plenty of sleep the night before.
|
|
|
T 10/28/08
|
HW due: Read §5.1; write §4.6 #7, 8, 9, and be ready
for a possible open-notes quiz on §5.1.
|
|
|
W
10/29/08
|
HW due: Read §5.2; write §5.1 #1, 5, and problem A1
below. I will post a solution to #1 on hwstore.org, and you may adapt that solution
if you wish.
Remember, indirect proof always involves assuming (bwoc) the negation of the
conclusion and showing that that leads to a contradiction. The letters “bwoc”
are an abbreviation for “by way of contradiction,” and you may use that
abbreviation in your proofs.
Additional problem A1:
Given: Mr. Hansen drives to work.
Mr.
Hansen’s car does not have a keyless ignition option.
Mr.
Hansen has hooked his keys onto his umbrella, in his office.
Prove: Mr. Hansen will not forget his umbrella at the office.
[A paragraph proof is acceptable.]
|
|
|
Th
10/30/08
|
HW due: Read §5.3; write §5.1 #5 if not already
finished (see hwstore.org for Sope’s version if necessary), §5.2 #2, 3, 4, 5,
6, 8, §5.3 #3, 4, 5, 7, 10, 27. Because this is a double-section assignment,
you may postpone a few of these problems until tomorrow if you run out of
time.
Note: Feel free to use the
abbreviations “alt. int.,” “alt. ext.,” “corresp.,” and “SSOT” in your
proofs. An example of a reason in a §5.2 proof would be (after proving angles
congruent) to say something like this:
7. l || m Reason
7. Alt. int. 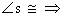 || lines || lines
An example of a reason in a §5.3 proof would be (after proving lines
parallel) to say something like this:
13. 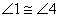 Reason
13. || lines Reason
13. || lines 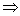 corresp. corresp. 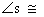
|
|
|
F
10/31/08
|
End of first quarter.
HW due: Read §5.4 and finish the double assignment (§5.2 #2, 3, 4, 5, 6, 8, §5.3
#3, 4, 5, 7, 10, 27).
Optional bonus assignment, highly
recommended for students who are in grade trouble:
Use Geometer’s Sketchpad to execute the following steps. For full credit, you
must demonstrate to me that you can quickly do all of the following, without
fumbling. In other words, you must practice during Math Lab or before school,
since there is no way you would be able to do all of these steps without
practice.
1. Place points A, B, C randomly on the screen.
2. Construct lines (not segments)
joining all pairs of points.
3. Construct the orthocenter and label it as ORTH. Do not hide the altitudes.
4. Construct segments AB, BC, and AC, and make them thick and red so that
they stand out.
5. Construct the three perpendicular bisectors for triangle ABC. Set their
appearance back to thin and black so that they do not stand out especially
forcefully.
6. Construct point CC (circumcenter) at the intersection of any two
perpendicular bisectors from step 4. Note that the third perpendicular
bisector serves as a double-check on your work.
7. Construct the circumcircle, and make it blue.
8. Construct the midpoint of the segment that connects CC and ORTH. Label
this midpoint as NPC (nine-point center).
9. Construct the nine-point circle, and make it green. It should pass through
the feet of the altitudes, the midpoints of the sides of the triangle, and
the three Euler points. (Euler
points are located midway between ORTH and A, midway between ORTH and B, and
midway between ORTH and C.)
10. Label the three Euler points as E1, E2, and E3.
|
|