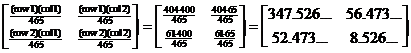STAtistics / Mr. Hansen 5/1/2008

Name: _________________________

“Everything Test” II

• Illegible or cryptic responses may not earn full credit, even if your answers are “correct.”
• Give all final numeric answers correct to at least 3 significant digits (AP standard).
• Circle or box your final answer if applicable (AP standard).
• Do not erase large sections. If you wish for a section to be ignored during grading, simply mark it through with a single large “X” and proceed. This is also an AP standard.
• Check here to indicate that you have read these instructions and understand them: o

Part I: Problems (20 pts. for #1, 30 pts. for #2)

1.	A workplace of 465 full-time employees (400 men and 65 women) contains a surprisingly large number of left-handed women. At the = 0.05 level, is there evidence of an association between gender and handedness at this company?
	Dominant Hand	M	F
	Right	88%	80%
	Left	12%	20%
	Set up and execute a suitable statistical test. Show adequate justification for your conclusion, including showing that you know the assumptions and have checked them. It is not necessary to show every little nitnoid detail. For example, when computing the contributions to chi-square, you may show one or two of the calculations and let your calculator do the rest.

2.	Here is part of the computer output from a study to see whether Joe Shilabotnik’s career RBI numbers were associated with his years of experience over his long 25-year baseball career. There are 25 data points that associate his playing year with runs batted in (RBI).
	Response variable: RBI Predictor Coef SE Coef T P Constant 35.420 8.951 3.96 0.001 Year 1.0385 0.6021 1.72 0.098 S = 21.71 R-Sq = 11.5% Analysis of Variance Source DF SS MS F P Regression 1 1401.9 1401.9 2.97 0.098 Residual Error 23 10839.9 471.3 Total 24 12241.8
(a)	We wish to develop a confidence interval for the true slope () of the linear regression relationship between playing year and RBI. Circle the relevant degrees of freedom that we will need to use.
(b)	The t statistic of the slope equals ______________ .
(c)	The standard error of the slope equals ______________ .
(d)	How can you tell that the value of the linear correlation coefficient (statistic) is positive?
(e)	The linear correlation coefficient equals ______________ .
(f)	Compute a 95% confidence interval for the true value of the slope. You may assume that all appropriate assumptions have been met. Show work.
(g)	Interpret the slope in the context of the problem.
(h)	Predict the number of runs batted in (RBI) during Shilabotnik’s tenth year of play. Show a wee bit of work.

Solutions:

1.	[We do not define parameters for a 2-way test.] H0: Gender and handedness are independent at this company. Ha: Some association exists between gender and handedness at this company. Assumptions for 2-way test or independence test [must identify by name!]:       Census acceptable? Yes. [This is not an SRS.]       All exp. counts 1, no more than 20% of them 1? Yes (see below). In fact, all exp. counts are 8. Observed counts: Expected counts: Test statistic: P-value = 0.0764 Conclusion: There is insufficient evidence ( = 3.14, df = 1, P = 0.0764) of an association between gender and handedness.
	Scoring:      4 pts. for hypotheses      4 pts. for assumptions and identifying name of test      4 pts. for test statistic (–2 if there was no attempt to explain how computed)      4 pts. for P-value      4 pts. for conclusion in context
2.	[This problem was remarkably similar to the previous day’s problem.]
(a)	df = n – 2 = 25 – 2 = 23
(b)	t = 1.72 (given)
(c)	(given)
(d)	b1 = 1.0385 > 0
(e)	Since r^2 = 0.115, r = 0.339.
(f)	m.o.e. = We are 95% confident that the true LSRL slope () is 1.0385 1.246. Alternate format: 95% C.I. for true LSRL slope () is (–0.2075, 2.2845). [Note: The problem did not ask for an additional conclusion, but do you see that because the C.I. includes 0, there is doubt as to whether the true slope is even positive at all?]
(g)	For every additional year of Shilabotnik’s career, the model predicts his RBI production to increase by 1.0385 runs.
(h)
	Scoring:      3 pts. ea. for all parts except (f) and (g)      6 pts. for (f)      6 pts. for (g), with 2 pts. deducted if student forgot “the model predicts”