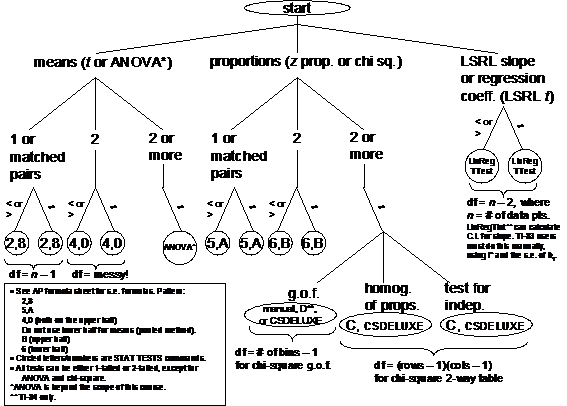|
T 4/1/08
|
HW due:
Click here. If you do not have time to finish
the reading assignment, then at least do #4 without the NMAP ratings. The
entire assignment will be spot-checked today (to make sure you are making
progress) and collected tomorrow.
|
|
|
W 4/2/08
|
HW due:
Completed assignment from yesterday.
|
|
|
Th 4/3/08
|
HW due:
Read the STAT TESTS summary
handout and start committing it to memory; write #11.16, 11.26, 11.62, 11.64.
By the time of the AP exam, you will need to have memorized essentially all
of the handout. We do not use STAT TESTS 1, 3, 7, 9, D, or F in our class.
Quiz (10 pts.) on the taxonomy
chart presented in class on April Fool’s Day. Given a scenario involving
proportions or means, number of tails (1 or 2), and number of samples (1, 2,
or more than 2), determine what test or tests would be appropriate. Your
choices will be the following:
STAT TESTS 1 (trick answer—not used)
Choice of “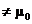 ” or “ ” or “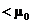 ” or “ ” or “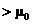 ” ”
STAT TESTS 2 with same set of hypothesis choices
STAT TESTS 3 (trick answer—not used) with same set of hypothesis choices
STAT TESTS 4 with same set of hypothesis choices
STAT TESTS 5 with same set of hypothesis choices
STAT TESTS 6 with same set of hypothesis choices
STAT TESTS F
CSDELUXE (chi square)
The final question on the quiz (asked and answered during class on 4/2)
concerns how to respond to the “Pooled” prompt that appears near the bottom
of STAT TESTS 4. If you did not happen to hear the answer, ask classmates
until you can track down someone who knows the answer. I was quite clear on
how to handle this situation and repeated the answer several times, but I am
getting somewhat tired of having to repeat myself. (Please note: Repeating
for clarification is fine, and that is part of what I am hired to do.
However, repeating for the sake of people who were not paying attention is
something I prefer to avoid.)
|
|
|
F 4/4/08
|
HW due:
Patch up the problems due yesterday, which will be collected and scored at
somewhere between 4 and 16 points. Then write #12.38, 12.40.
Note: By vote of the small number
of people who attended class on Friday, the collection of last Thursday’s
assignment was postponed until Monday. However, note that there is an
additional multi-part assignment due Monday.
|
|
|
M 4/7/08
|
HW due (you may choose any 2 parts, or do all 3 for
a small bonus):
1. Purchase a small bag of M &M’s plain candies, and bring it to class.
2. Reread the STAT TESTS summary
handout and continue committing it to memory
3. Read pp. 700-709.
|
|
|
T 4/8/08
|
HW due:
1. If you have not already done so, enter or download the CSDELUXE (chi-square deluxe)
program.
2. Use CSDELUXE to redo yesterday’s in-class problem, which was a chi-square
goodness-of-fit problem involving M&M’s candies. Be sure to execute all
the PHASTPC steps. Hopefully, it will go much faster the second time,
especially since CSDELUXE does most of the computation for you.
H0: pblue = .24, pbrown
= .13, pyellow = .14, pred = .13, porange = .2, pgreen = .16
Ha: The probabilities
are not all as claimed.
Observed counts: 86 blue, 56 brown, 49 yellow, 51 red, 73 orange, and 72
green candies.
3. A regular hexahedral randomizer is rolled 100 times, resulting in the
following data:
Roll of 1: 20 times
Roll of 2: 17 times
Roll of 3: 13 times
Roll of 4: 10 times
Roll of 5: 19 times
Roll of 6: 21 times
Is there any evidence that this die is unfair? Perform a goodness-of-fit
test, showing all PHASTPC steps.
4. Suppose that the trends observed in #3 continue for another 100 rolls. In
other words, perform these steps:
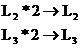
(You have now multiplied the expected and observed counts by 2, making n = 200.) There is no need to perform
a complete PHASTPC this time. What is the new P-value?
5. In #4, use nonmathematical language to explain why it is believable that
the test shows statistical significance when n = 200 but not when n
= 100.
6. Examine the contributions to chi-square to determine which roll(s) most
strongly suggest a lack of randomness.
|
|
|
W 4/9/08
|
HW due:
Use CSDELUXE to help you as you solve the following two problems using full
PHASTPC procedures. Be sure to show your work as you calculate several of the
expected cells (the ones that CSDELUXE stores in matrix [B]). The formula for
an expected cell in a 2-way table is cell = rowtotal · coltotal
/ grandtotal, and df (degrees
of freedom) can be calculated by (rows – 1)(cols – 1). For other
helpful hints, see the STAT TESTS
Summary handout.
1. Use PHASTPC to see if there is any evidence of a relationship between hair
color and type of college attended for the 72 faculty members at St. Snively
School. (These data are made up.)
Blondes: 16 attended state schools, 4 attended private colleges (non-Ivy
League), 8 attended Ivy League
Brunettes: 13 state, 6 private non-Ivy, 2 Ivy
Other: 11 state, 8 private non-Ivy, 4 Ivy
2. There are 324 students in the St. Snively Upper School. Members of the
Class of 2009 complain that Mr. Hinson is referring them too often to Mr. N.
Dre Olé for dress code violations. They produce the following data, proving
that juniors are indeed the most likely students to be referred to the dean:
Class of 2008: 32 students referred, 46 not
Class of 2009: 38 students referred, 42 not
Class of 2010: 39 students referred, 45 not
Class of 2011: 31 students referred, 51 not
(a) Prove (using PHASTPC) that there is no evidence of an association between
class year and likelihood to be referred to the dean.
(b) Even if such an association existed, would that constitute evidence of
bias on Mr. Hinson’s part? Explain briefly.
|
|
|
Th 4/10/08
|
HW due:
Read pp. 752-757 and the STAT
TESTS handout (especially the second-to-last row, which summarizes the
“LinRegTTest” feature of your calculator); write (a) through (e) on pp.
752-753.
Quiz (10-20 pts.) will cover
either the chi-square procedures, the rudiments of the STAT TESTS handout, or
both.
Sample questions:
1. Which tests do we not use?
Answer: 1, 3, 7, 9, D, and F. The z tests and intervals involving means
(1, 3, 7, and 9) are not used, because z
tests for means make the unrealistic assumption that 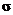 is known. We do not
use D and F, because they are beyond the scope of our course. However, we do
use 5, 6, A, and B, which are z
tests for proportions. is known. We do not
use D and F, because they are beyond the scope of our course. However, we do
use 5, 6, A, and B, which are z
tests for proportions.
2. Which test is equivalent to a chi-square 2-way test having 1 degree of
freedom?
Answer: 2-tailed 2-prop. z
Explanation: If df = 1, we can
conclude that the number of rows is 2, and the number of columns is also 2.
Therefore, this is akin to checking to see if juniors have a different
likelihood of being referred to the dean when compared to other students.
(Categories are “junior” and “non-junior” crossed with “referred” and “not
referred.”) The null hypothesis is that juniors and non-juniors are equally
likely to be referred, i.e., no evidence of an association. Another way to
say this is that junior/non-junior status is independent of referred/non-referred status. However, all of this
could equally well be written up as a 2-tailed 2-prop. z test with hypotheses as follows:
Let p1 = true
probability of being referred, given that a student is a junior
Let p2 = true
probability of being referred, given that a student is not a junior
H0: p1 = p2
Ha: 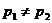
|
|
|
F 4/11/08
|
HW due:
Write an answer to the questions below, and read pp. 757-767 and 774-779.
This concludes our reading from the textbook.
Question 1: What do the following symbols stand for? 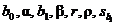
Question 2: Why is a LSRL t test
for 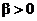 equivalent to a LSRL
t test for equivalent to a LSRL
t test for 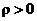 ? ?
Quiz (10 pts.) on the STAT TESTS
taxonomy is likely. Note that we now have a third branch at the top for the
LSRL t test.
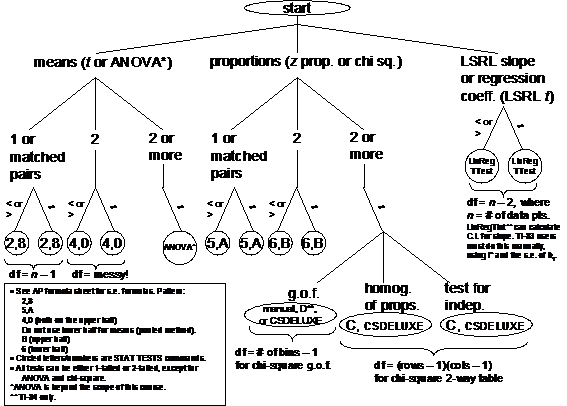
|
|
|
M 4/14/08
|
HW due:
Read all the notes and hints shown below; write #14.7, 14.9.
Notes and hints:
14.7. Perform the full PHASTPC method, not merely the HTPC steps listed. When
checking assumptions, use the techniques given in class last Friday.
Specifically, that means using a resid. plot and r to show that the true relationship is linear, using a histogram
or NQP to show that the resids. are normally distributed, and using a
scatterplot to show that the s.d. of the response variable about the LSRL
does not vary with x.
14.9. Part of what you have to do on the AP exam is to decode computer output
as shown here. The first row is a row of headings: variable, coefficient,
s.e. of coefficient, t-ratio (i.e.,
the value of t), and probability
(i.e., P-value).
The second row, labeled “Constant,” gives information for the LSRL y-intercept. We note that the y-intercept (called b0 by the AP people) is
–61.1209 in this problem, and then we
ignore the rest of the line. That’s
right, we ignore it. There is nothing useful there that will help us on the
AP exam.
The final row, labeled “year,” gives information for the LSRL slope. In order
from left to right, these values are b1
(i.e., the computed slope itself), s.e. of slope (denoted 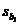 ), t statistic
from the LSRL t test, and P-value of the LSRL t test. ), t statistic
from the LSRL t test, and P-value of the LSRL t test.
One of my favorite test questions is to give a problem such as #14.9, except
with 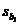 missing. Good
students know that missing. Good
students know that 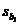 can be computed by
the formula can be computed by
the formula 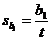 , but mediocre students may flop around for half an hour
trying to compute , but mediocre students may flop around for half an hour
trying to compute 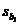 using the impossibly
difficult formula provided on the AP formula sheet. You need using the impossibly
difficult formula provided on the AP formula sheet. You need 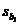 in order to answer
part (c), since a C.I. for slope is calculated in the exact same way as any
other C.I. we have studied, namely C.I. = est. in order to answer
part (c), since a C.I. for slope is calculated in the exact same way as any
other C.I. we have studied, namely C.I. = est. 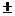 m.o.e., where m.o.e.
= (critical value)(s.e.). m.o.e., where m.o.e.
= (critical value)(s.e.).
In #14.9(c), all you have to do is use the calculated value of b1 as your estimate, the t* value from Table C as your critical
value, and 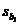 as your standard
error. However, you must show your formulas, plug-ins, and answer in order to
earn points. Merely copying the answer from the back of the book will earn
you a zero. as your standard
error. However, you must show your formulas, plug-ins, and answer in order to
earn points. Merely copying the answer from the back of the book will earn
you a zero.
|
|
|
T 4/15/08
|
No class (Diversity Day).
However, life goes on. The assignment below should be completed as your HW
for today and will be collected Wednesday.
HW due: Write #14.11abcde,
14.18abcd.
|
|
|
W 4/16/08
|
HW due:
Print out the AP
formula sheet (pages 16, 17, 18, and 21 only; do not print the entire
document!) and mark it up as follows, where X means a waste of ink, OK means you
should circle it lightly, and !! means important (bold circle or double
circle). For full credit, you must write the parenthetical comments on your
formula sheet as well.
I. Descriptive Statistics
on p. 16 of the .PDF file (marked 11 in lower right corner)
1st formula: X (we have known how to find a sample mean
since at least B or A form)
2nd formula: X (this is s.d., which the calculator finds by
STAT CALC 1)
3rd formula: X (this is the pooled estimate of standard
error, which we never use, since we never “pool”)
4th formula: OK (LSRL; note that the AP consistently uses b0 for intercept and b1 for slope,
not a and b)
5th formula: X (we never calculate b1 this way; use STAT CALC 8 instead)
6th formula: !! (since LSRL always passes through 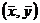 , we can solve for b0
by plugging in) , we can solve for b0
by plugging in)
7th formula: X (use STAT CALC 8 with Diagnostic On to find
this instead)
8th formula: !! (a key formula that ties together b1, r, and the s.d. of x
and y; be sure that your algebra is
strong enough so that you can solve for any missing quantity if given the
other 3)
9th formula: X
Note: After you have crossed out
the 9th formula, replace it with the much more useful formula 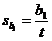 . .
II. Probability on p. 17 of
the .PDF file (marked 12 in lower left corner)
1st formula: !! (always true; can also be written as 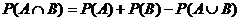 if needed) if needed)
2nd formula: !! (conditional probability formula; can be
written 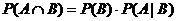 ,
which is always true, unlike the “fake” formula ,
which is always true, unlike the “fake” formula 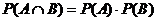 , which is true only for independent events) , which is true only for independent events)
3rd formula: !! (def. of expected value, a.k.a. mean of a
random variable)
4th formula: !! (def. of variance of a random variable)
5th formula: OK (same as binompdf(n,p,k) except that you cannot show calc.
notation on AP)
6th formula: OK (common sense tells you this: expected # of
successes = # of trials · prob. of success)
7th formula: !! 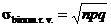
8th formula: OK (expected value of the sample proportion =
true probability)
9th formula: !! 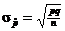
10th formula: OK (expected value of the sample mean = true
mean)
11th formula: X (This formula is not true as stated! If n is large, then CLT tells us that the
formula is approximately correct. If the population is exactly normal, then
the formula is true regardless of the value of n.)
12th formula: !! We usually write this as 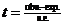 or or 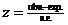 , where s.e. comes from next page. , where s.e. comes from next page.
13th formula: !! Note that we write the second part as
(critical value) · (s.e.) = m.o.e.
III. Single-sample and two-sample
standard error formulas on p. 18 of the .PDF file (marked 13 in lower
right corner)
Box 1: STAT TESTS 2, STAT TESTS 8
Box 2: STAT TESTS 5, STAT TESTS A
Box 3, upper half: STAT TESTS 4, STAT TESTS 0
Box 3, lower half: X (not used since we never use the
pooled method)
Box 4, upper half: STAT TESTS B
Box 4, lower half: STAT TESTS 6
Table B (t distribution critical values) on p. 21 of the .PDF file
(marked 16 in lower left corner)
The only change you need to make here is to cross out the 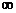 symbol in the lower
left corner and replace it with z*
so that the table matches your textbook’s Table C at the very end of the
book. symbol in the lower
left corner and replace it with z*
so that the table matches your textbook’s Table C at the very end of the
book.
|
|
|
Th 4/17/08
|
HW due:
Read the Must-Pass Quiz and
start familiarizing yourself with its contents. Everyone must pass this quiz
before the end of the semester.
Written problems from last week and this week may be collected and/or scanned
a second time. Your marked-up formula sheet may be scrutinized more closely.
The double quiz originally scheduled for today has been postponed until
tomorrow.
In class: Lower School Science Fair scavenger hunt.
Loose end from yesterday’s class:
Because of my copying error (when most of the class except for Matt failed to
notice that I had used the intercept instead of the slope at one point),
there was a cascade of errors. Here is the corrected work to put in your
notes.
n = 44
df = n – 2 = 42
b0 = .661734
b1 = .492749
r = .6478
Assess the significance of the linear
regression coefficient.
Let 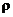 = true lin. correl.
coeff. for the relationship. = true lin. correl.
coeff. for the relationship.
H0: 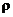 = 0 = 0
Ha: 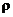 > 0 > 0
Assumptions were tested in class and found to be satisfied (mostly).
t = 5.510978
P < 10–6
Conclusion: We must proceed with caution, since there is some indication that
the standard deviation of responses varies with x. With that caveat, however, there is strong evidence (t = 5.51, n = 44, P < 10–6)
of a positive linear correlation between interest and perceived usefulness of
the Diversity Day components. In other words, students who are more
interested see more usefulness on average, and students who are less
interested see less usefulness on average, and the relationship is roughly
linear.
Compute an 85% C.I. for the true
slope, 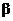 : :
t* = 1.466352899 (estimated
from Table C, or computed exactly by INVT)
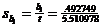 = .0894123 = .0894123
m.o.e. = (t*)(s.e.) =
(1.466352899)(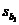 ) = (1.466352899)(.0894123) = .131 ) = (1.466352899)(.0894123) = .131
Conclusion: We are 85% confident that the true increase in the usefulness
rating per unit of increase in the interest rating is .493 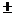 .131. .131.
Alternate format for conclusion: We are 85% confident that the true increase
in the usefulness rating per unit of increase in the interest rating is in
the interval (.362, .624).
|
|
|
F 4/18/08
|
Double Quiz
(10 + 10) on the formula sheet and questions drawn randomly from the Barron’s
AP review book. From now until further notice, bring the Barron’s book to
class each day and leave your blue textbook at home.
HW due: Scavenger hunt findings.
If you were not able to participate in the scavenger hunt, then write up a
set of eight (8) imaginary Lower School Science Fair projects exhibiting a
possibility for using each of the following statistical tests. The first one
has been done for you as an example.
2-sample t test: “Global Warming:
Helpful? or Harmful?” Student investigates whether plants grown in a CO2-rich
environment grow taller on average than control plants.
1-sample t test:
______________________________________________________________________
2-prop. z test:
______________________________________________________________________
1-prop. z test:
______________________________________________________________________
LSRL t test:
______________________________________________________________________
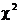 g.o.f.:
______________________________________________________________________ g.o.f.:
______________________________________________________________________
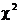 2-way:
______________________________________________________________________ 2-way:
______________________________________________________________________
ANOVA: ______________________________________________________________________
During yesterday’s scavenger hunt, I was able to find at least one example of
every type except for the 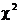 g.o.f. test. Of
course, I stayed longer than the rest of you. By 11:35, the end of E period,
I had found only six. g.o.f. test. Of
course, I stayed longer than the rest of you. By 11:35, the end of E period,
I had found only six.
|
|
|
Week of 4/21/08
|
Must-Pass
Quiz begins in earnest.
Everyone will receive an SRS of several questions. This is a great way to
review for the AP exam. The Must-Pass Quiz is required of all students in
order to pass the course. A link to the answer key is provided on the MPQ
page.
Note: Everyone who is planning to
take the AP exam should also be spending 30-40 minutes a night working problems
in the Barron’s book. If you are not willing to make that time commitment,
please do yourself a favor and tell Mr. Andreoli right now that you will not
be taking the exam. It’s too late to get a refund, but at least you won’t
have any guilt issues to wrestle with.
|
|
|
M 4/28/08
|
No school (Phi Beta Kappa
day).
|
|
|
T 4/29/08
|
HW due:
Read this
recent newspaper article and answer questions 1 through 4 below.
Perform all steps: PHASTPC for #2, PA*MC for #3. Note: PA*MC stands for defining the parameters, checking assumptions,
finding the critical value (z* or t*), computing the margin of error from the
formula m.o.e. = (crit. value) (s.e.), and writing a conclusion in the context of the problem.
Warning: Remember that you will use
a different s.e. formula in #2 from the one you will use in #3. Both formulas
are given on your AP formula sheet.
For full credit, write out the assumptions both times. Yes, I realize that
this is redundant, but the purpose is educational: You need practice checking
assumptions.
1. How large is the observed difference between obesity likelihood for short
sleepers versus long sleepers? Be sure to use proper statistical notation
(and an “=” sign) when stating this difference.
2. Is there statistically significant evidence that short sleepers are more
likely to develop obesity than long sleepers?
3. Find a 95% confidence interval for the size of the increased obesity
likelihood that short sleepers have, relative to long sleepers.
4. Neither the article nor its headline states that short sleeping causes
obesity. Why not?
|
|
|
W 4/30/08
|
Everything Test I
(100 pts.). Chi-square tests and
LSRL t tests will be emphasized,
but all questions from the Barron’s review book for the entire year are fair
game. The format will be predominantly multiple-choice.
|
|