|
M 3/3/08
|
HW due: Read
pp. 592-608. Omit the exercises for now, but be sure to read and work through
the examples (11.1 on p. 593, 11.2 on p. 594, 11.3 on pp. 599-600, and 11.4
on pp. 607-608). Instructions are given below. Leave all lists in your
calculator so that I can verify that you actually performed the steps.
Example 11.1, p. 593
Enter the 5 given values into L3 and then push the following
buttons: STAT TESTS 8 Data L3 1 .95 Calculate ENTER. That should
give you the C.I. in the interval format (18.687, 70.193), which is
consistent with the book. Then, use your calculator to find the m.o.e. by the
formula
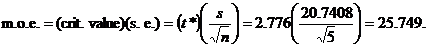
Observe that the “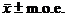 ” format, namely ” format, namely 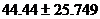 , is almost exactly equal to the interval format computed above.
The slight difference can be attributed to rounding error in the table value
of t*. We do not worry about minor
differences like this. Remember: “In statistics, approximations are OK.” , is almost exactly equal to the interval format computed above.
The slight difference can be attributed to rounding error in the table value
of t*. We do not worry about minor
differences like this. Remember: “In statistics, approximations are OK.”
Example 11.2, p. 594
Enter the 10 given data values into L4 and then push these
buttons: STAT TESTS 2 Data 0 L4 1 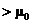 Calculate ENTER. Calculate ENTER.
Observe that the t statistic is
2.697, which agrees with the book’s calculation. Also observe that the P-value of the test is .01226, which
also agrees..
Example 11.3, pp. 599-600
Enter only the 20 gain values into
L5 (2, 0, 6, 6, 3, 3, 2, 3, –6, 6, etc.). The reason is that we do
not have two independent samples: The same people were sampled twice, and our
concern is whether the mean difference
is statistically significant. Then push the following buttons: STAT TESTS 8
Data L5 1 .9 Calculate ENTER. That should give you the C.I. in the
format (1.3815, 3.6185). Since 0 is not in the interval, a two-tailed test of
significance would clearly succeed.
Then perform a one-tailed test (earlier on p. 600) as follows: STAT TESTS 2
Data 0 L5 1 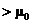 Calculate ENTER.
This should give you a P-value of
.0005216, which differs slightly from the book’s value of .00053. The likely
reason for the discrepancy is that statistical software, in order to be
conservative, should always round P-values
up. Calculate ENTER.
This should give you a P-value of
.0005216, which differs slightly from the book’s value of .00053. The likely
reason for the discrepancy is that statistical software, in order to be
conservative, should always round P-values
up.
For example, if a test had a P-value
of .0500047899959, and if we were forced to round to 5 decimal places because
of space limitations, we would prefer to round to .05001 even though you were
taught to round to .05000 in other courses. The reason is that if 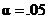 ,
reporting the P-value as .05000
would erroneously suggest that statistical significance was achieved, when in
fact the cutoff value was exceeded. However, the ethos of our course (“in
statistics, approximations are OK”) is at odds with the absurd notion that a
difference this small could matter. It is simply a philosophical principle that if one is forced to round a P-value, all rounding should be
conservative (i.e., upward) in order to avoid overstating the case for
statistical significance. ,
reporting the P-value as .05000
would erroneously suggest that statistical significance was achieved, when in
fact the cutoff value was exceeded. However, the ethos of our course (“in
statistics, approximations are OK”) is at odds with the absurd notion that a
difference this small could matter. It is simply a philosophical principle that if one is forced to round a P-value, all rounding should be
conservative (i.e., upward) in order to avoid overstating the case for
statistical significance.
Example 11.4, pp. 607-608
Simply read this one. There are no buttons to push.
|
|
|
T 3/4/08
|
HW due: If
you have not already done the assignment that was due yesterday, then do it. Also due today (from each of
the 5 groups) is a statement of methodology (approx. 1 page) for the quickie
experiment involving the release of a standard ruler. We will all use 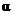 = .05 as our cutoff
value for statistical significance. = .05 as our cutoff
value for statistical significance.
Jack, Matt, Willie: control = dominant hand, experimental =
non-dominant hand
Alex, Kevin, Michael: control = regular, experimental = blindfolded
with audio cue only
Alek, Charlie, John: control = regular, experimental = defined
distracting ambient noise*
William, J.D., Gleb: control = regular, experimental = defined loud
iPod music
Lawton, Bobby: control = regular, experimental = while balancing a
nearly full cup of water
If you wish to change your environmental alteration, please wait until Wednesday.
You should press ahead using your current statement of methodology for the
moment.
In class: Run pilot tests and calculate the standard deviation of the difference between subjects’ mean
readings. Try also to compute the power of the t test against the alternative that you think is likely, based on
your pilot testing.
* Changed to spinning a lanyard in a defined fashion while performing the
ruler-catch test.
|
|
|
W 3/5/08
|
HW due: Submit
your pilot-test raw data in a neat tabular format, along with your estimate
of the sample size that will be needed in order to have good power against
the alternative that your pilot testing suggests is likely. Remember to
calculate s.e. using the formula 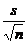 , where s = s.d.
of differences. , where s = s.d.
of differences.
|
|
|
Th 3/6/08
|
HW due:
Each group should make a second try at estimating the power of the t test. Specific instructions are
given below. Your methodology writeups should be also be prepared for
collection. Yesterday’s submission has been photocopied, and the original was
returned to your group leader’s mailbox.
Jack, Matt, Willie:
Use a 2-sided alternative hypothesis. Assume that 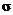 = 2 cm
(conservatively), and compute the power against the = 2 cm
(conservatively), and compute the power against the 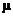 = 1.36667 cm
alternative for n = 15 and n = 23. In class yesterday, we showed
that the power was about 83% when n
= 20. There seems to have been a bug in the raw data that we wrote on the
board yesterday, since the sample mean is actually 1.36667. = 1.36667 cm
alternative for n = 15 and n = 23. In class yesterday, we showed
that the power was about 83% when n
= 20. There seems to have been a bug in the raw data that we wrote on the
board yesterday, since the sample mean is actually 1.36667.
Alex, Kevin, Michael:
Use a 1-sided alternative hypothesis. Assume that 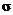 = 7 cm
(conservatively), and compute the power against the = 7 cm
(conservatively), and compute the power against the 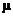 = 7.11111 cm
alternative for n = 10 and n = 15. = 7.11111 cm
alternative for n = 10 and n = 15.
Alek, Charlie, John:
Use a 1-sided alternative hypothesis. Assume that 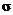 = 6 inches
(conservatively), and compute the power against the = 6 inches
(conservatively), and compute the power against the 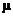 = 5.04167 inch
alternative for n = 13 and n = 19. = 5.04167 inch
alternative for n = 13 and n = 19.
William, J.D., Gleb:
Use a 2-sided alternative hypothesis. Assume that 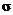 = 7 cm, and compute
the power against the alternative of = 7 cm, and compute
the power against the alternative of 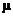 = –0.9875 cm for n = 21 and n = 51. Your test, based on the pilot, may lead to a finding of
“no statistically significant effect observed,” which means that you may need
to select a different alternative environment if you want to prove
statistical significance. It is OK to leave things as they are, however.
Sometimes it is very interesting to find no evidence for an effect that
everyone assumed would be present. = –0.9875 cm for n = 21 and n = 51. Your test, based on the pilot, may lead to a finding of
“no statistically significant effect observed,” which means that you may need
to select a different alternative environment if you want to prove
statistical significance. It is OK to leave things as they are, however.
Sometimes it is very interesting to find no evidence for an effect that
everyone assumed would be present.
Lawton, Bobby:
Use a 1-sided alternative hypothesis. Assume that 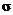 = 3 cm, and compute
the power against the = 3 cm, and compute
the power against the 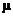 = 3.22222 cm
alternative for n = 5 and n = 12. = 3.22222 cm
alternative for n = 5 and n = 12.
|
|
|
F 3/7/08
|
HW due:
Corrected power computations as assigned for yesterday. Before submitting
your paper, please stop by to see me to make sure that your power
computations are correct. I will be available at the times listed below. If
not all members of your group can make it, be sure to send at least one.
Thursday 3/6: 2:30 to 3:00 p.m.
Friday 3/7: 7:30 to 8:00 a.m., 9:45 to 10:25 a.m.
|
|
|
M 3/10/08
|
HW due:
Write #11.60, 11.62, 11.63. Use the PHASTPC
format for #11.63c.
|
|
|
T 3/11/08
|
Triple Quiz (30 pts.) on all recent material.
|
|
|
W 3/12/08
|
Senior career day (no
class).
|
|
|
Th 3/13/08
|
No additional HW due. You should
be working on your group project. A bonus of 5 points per group member will
be provided if you submit your project today.
|
|
|
F 3/14/08
|
(Pi Day, also the end of
the third quarter)
All typos, crossword puzzles, and
other extra credit of any type must be given in person to Mr. Hansen by noon
today. Late submissions, as well as submissions left in the office or in
the mailroom, will be applied toward the fourth quarter.
Ruler-catching experiment writeup is due at noon. Extension requests will
be considered, but as we discussed in class, no extension will be approved
for a longer period than the amount of time remaining before the deadline.
For example, a 1-day extension request made Thursday at noon might be
approved if it is a worthy request, but a request made today (Friday) at
11:15 a.m. would be for a maximum of 45 minutes, i.e., extending the deadline
to 12:45 p.m. The rationale is that if you are working all along, you would
surely realize by x hours before
the deadline that you have more than 2x
hours of work remaining. Realizing only at the very end that you are, say, a
day behind is illogical and, if you have been working incrementally,
impossible.
The project writeup is worth a maximum of 100 points per student. The
following elements are required for full credit:
1. Title that summarizes the research question. (Example: Does Singsong-Like Chitchat Adversely
Affect Ruler-Catching Performance?)
2. Methodology, edited in accordance with the comments you received at the
beginning of the week.
3. Explanation of why you chose the sample size you did.
4. Summary statistics (sample means and sample standard deviations for
control, altered environment, and difference; 95% confidence interval for the
true difference).
5. One-sample t test presented in
the popular PHASTPC format.
Remember, the conclusion must be
stated in the context of the problem. You cannot say something like, “We
found sufficient evidence to reject the null hypothesis” and leave it at
that.
6. Appendix containing release sheets from your test subjects and all raw
data (one row per subject).
7. Group leader report justifying the recommended point split among group
members. This report must state what each person did. It is not sufficient to
say, “We all worked equally on the project and deserve equal points.” If this
report is missing, the group leader’s score will be reduced by 10 points.
|
|
|
M 3/31/08
|
Classes resume.
|
|