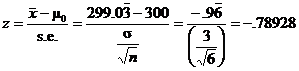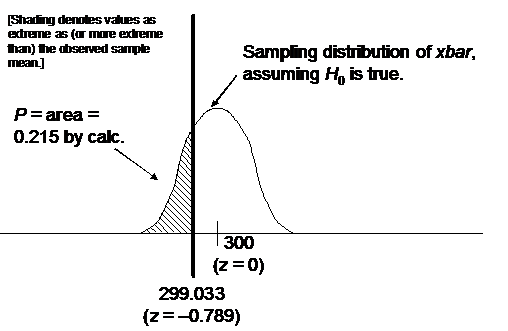|
F 2/1/08
|
HW due: Read pp. 506-518 twice. This material needs to be
read closely and carefully. Take good notes (hint, hint).
|
|
|
M 2/4/08
|
HW due
(but not to be collected until Tuesday): Read pp. 520-523 (highlight or underline the final two sentences on
p. 523, beginning with the words, “Do notice once again”); write #10.6, 10.7,
10.8. Some of the answers to the even-numbered questions are given below.
10.6(b) Since z* = 2.576 from Table C (inside back
cover), m.o.e. = 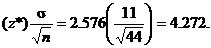
Now that you know the m.o.e., you should be able to find the mean and
therefore write the confidence interval. A confidence interval (C.I. for
short) can be written in either of two equivalent notations.
(1) The first is the interval notation that you learned in precal. For
example, if the C.I. is from 13.221 to 25.881, you would write (13.221,
25.881) or [13.221, 25.881] as your answer. (That is not the answer to this
problem, but you get the idea.) Your calculator produces answers in this
format by default when you use the command STAT TESTS 7, 8, 9, 0, A, or B.
(2) The second is what we might call the “estimate 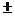 m.o.e” format. For
example, if the interval notation is [13.221, 25.881], then the estimate m.o.e” format. For
example, if the interval notation is [13.221, 25.881], then the estimate 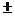 m.o.e version of the
answer would be 19.551 m.o.e version of the
answer would be 19.551 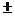 6.330. (That is not
the answer to #10.6. It is simply offered as an example of the format.) 6.330. (That is not
the answer to #10.6. It is simply offered as an example of the format.)
You need to be equally comfortable with both formats, since the AP exam uses
both. Your calculator uses only the first, but hopefully you can figure out
how to convert from one to another.
Do you understand the examples? If not, call a classmate or contact me
immediately. Shoot, call me or e-mail me during the Super Bowl; I almost
never watch football on TV. However, it is your responsibility to do something.
10.8(a) Since m.o.e. = 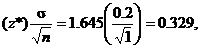 the C.I. is 3.2 the C.I. is 3.2 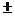 0.329. The
equivalent alternate format is [2.871, 3.529]. 0.329. The
equivalent alternate format is [2.871, 3.529].
10.8(b) This is very
similar to part (a), except with a different value for n. I am hoping you can do this on your own.
|
|
|
T 2/5/08
|
HW due: Read pp. 524-525, 527-528; write #10.16 (showing
work) and #10.17.
Open-Notes Quiz (10 pts.) on all
of §10.1. I will not answer any questions related to the two standard C.I.
formats (see yesterday’s calendar entry) after 3:30 p.m. on Monday, 2/4/08.
You will simply have to contact a classmate.
Comments on the assignment:
You should read pp. 524-525 several times and take careful written notes.
These two pages are probably the most hard-hitting, densely packed,
high-value-per-word paragraphs in the entire textbook.
On p. 527, the paragraph beginning with the words “The confidence level states . . .” needs some amplification. I would
have worded it as follows: “The confidence
level states the probability that the method
will give a correct answer. Contrary to what many people think, it does not
state the probability that a particular confidence interval is correct.
Suppose for the moment that the confidence level is 95%, as it often is. If
we were to compute many confidence intervals from many SRS’s (which seldom
happens in the real world, of course, since a poll or analysis is typically
carried out with only one SRS), then approximately 95% of the confidence
intervals so computed would contain the true parameter value. That is very
different from saying, “The probability is .95 that this particular C.I. contains the true parameter value.” The
quoted statement is actually nonsense; there is no way to compute such a
probability for a particular C.I., since the C.I. either does or does not
contain the parameter value, and we do not know what the parameter value is.
The reason for using the term “confidence” instead of “probability” is that
probability requires a long run, and there is no long run to be had in a
single confidence interval.
Please note that although computing a C.I. and computing the sample size
required to achieve a desired m.o.e. are techniques that are demonstrated in
the examples and exercises, they are perhaps the least important topics in
§10.1. After all, computing a z
confidence interval is a simple matter of punching buttons. Anyone can be
trained to do this . . .
Example: Suppose we gather data from an SRS of size 150. To
find the 95% C.I. for a mean when 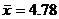 and and 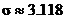 , all we need to do is to punch the following buttons. , all we need to do is to punch the following buttons.
STAT
Left arrow (to highlight “TESTS”)
7 (to choose “ZInterval”)
Highlight “Stats”
ENTER
Down arrow
3.118
Down arrow
4.78
Down arrow
150
Down arrow
.95
Down arrow
ENTER
Try it! If you have trouble, try again. If you fail several times in a row,
contact a classmate. If you still can’t figure out how to punch the buttons,
come to the Math Lab for help.
Remember, though, that the conceptual aspects of §10.1 are much more
important than the computational exercises. A good way to prepare for your
quiz is to read the section summary on pp. 527-528, taking time to reread
portions of the main text whenever you have the slightest confusion about
what the summary is saying.
|
|
|
W 2/6/08
|
No additional HW due. However, another open-notes
quiz is possible.
|
|
|
Th 2/7/08
|
HW due: Design an experiment to address the following research
question. We will stipulate in advance that the lack of blinding creates a
possible bias.
Does distracting “random number
chanting” increase the mean time required by STAtistics students to complete
a 25-question arithmetic quiz?
Each student must complete a methodology paragraph addressing control,
randomization, and replication. Be very specific so that nothing is left in
doubt. The best writeup will be executed during class, and we will see if the
results are statistically significant.
|
|
|
F 2/8/08
|
HW due: Read pp. 531-539; rewrite your methodology from
yesterday. Papers containing one or more words that need to be labored over
(i.e., deciphered because of some lack of clarity in handwriting) will be
returned ungraded. Handwriting is required.
|
|
|
M 2/11/08
|
HW due: Use the technique demonstrated in class Friday
(beginning each time with the all-important word “Let”) to define null and
alternative hypotheses for each of the following research questions, plus a
brief overview of what data will be gathered and why. The first two have been
done for you, but you should copy them as part of your assignment.
1. Does Barack Obama currently have a nationwide lead over Hillary Clinton
among likely voters in the fall 2008 election?
Let p1 = true proportion
of likely voters who currently prefer Barack Obama to Hillary Clinton
p2
= " " " " " " " " Hillary
Clinton to Barack Obama
H0: p1 = p2
Ha: p1 > p2
We will gather polling data for the sample proportions 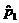 and and 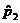 . Clearly, if . Clearly, if 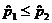 , we would find no evidence to support the research
question. (Note: That is different
from finding evidence disproving the research question.) On the other hand,
if , we would find no evidence to support the research
question. (Note: That is different
from finding evidence disproving the research question.) On the other hand,
if 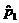 > >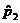 in our polling data,
we would need to analyze the H0
sampling distribution of in our polling data,
we would need to analyze the H0
sampling distribution of 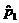 – –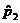 to see if the difference
is statistically significant. to see if the difference
is statistically significant.
Note: This is not the way polls are
conducted in real life. In real life, we do not have 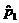 and and 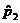 , since this notation presupposes independent samples. In
real life, we have only one sample. Therefore, the question posed cannot be
answered in real life by a two-sample hypothesis test. We would instead have
to develop a “benchmark” figure for one of the candidates (say, Hillary
Clinton) and then perform a one-sample test to see if there is evidence that
the other candidate (Barack Obama) exceeds the benchmark by a statistically
significant amount. , since this notation presupposes independent samples. In
real life, we have only one sample. Therefore, the question posed cannot be
answered in real life by a two-sample hypothesis test. We would instead have
to develop a “benchmark” figure for one of the candidates (say, Hillary
Clinton) and then perform a one-sample test to see if there is evidence that
the other candidate (Barack Obama) exceeds the benchmark by a statistically
significant amount.
Let us make up some numbers to illustrate this idea. Suppose Hillary
Clinton’s level of support is known to be 21.0%, and we have polling data
from an SRS of 843 voters showing that Barack Obama’s support 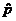 , is 22.3%. (We use , is 22.3%. (We use 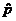 for Obama, not for Obama, not 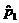 , because there is only one sample.) First, we must
formulate new null and alternative hypotheses: , because there is only one sample.) First, we must
formulate new null and alternative hypotheses:
H0: p = 0.21
Ha: p > 0.21
Next, we must check the rules of thumb:
population >> 10n = 10(843) =
8430? yes
np = 843(.223) = 188 > 10? yes
nq = 843(.777) = 655 > 10? yes
Next, if we are lazy, we can simply punch STAT TESTS 5 and run a 1-proportion
z test. Key in p0 = .21, since this is the hypothesized (Hillary
Clinton) comparison value. Key in 188 for x,
the observed count of successes, since this is the number of people in the
SRS who supported Obama. Key in n =
843. Finally, choose “>p0”
for the type of test, namely a one-sided test looking for support on the high
side of Clinton. Then highlight “Calculate” and press ENTER. The P-value is found instantly to be
0.1768.
Interpretation: Although Obama’s poll data seem to suggest a higher level of
support (22.3% vs. 21.0%), this difference is not statistically significant.
Even if Obama’s true support were exactly the same as Hillary Clinton’s,
namely 21.0%, we would see a sample proportion of 22.3% or higher for Obama
about 17.7% of the time. This is not rare enough to lead us to reject H0.
2. (Matched pairs.) Do foreign language tapes published by Company X make a
difference in students’ ability to learn vocabulary?
Let 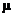 = true mean difference for each student (“with tapes” minus
“without tapes”) in number of vocabulary words learned per day = true mean difference for each student (“with tapes” minus
“without tapes”) in number of vocabulary words learned per day
H0: 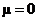
Ha: 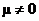
We will recruit volunteers and will have them learn their daily vocabulary with
tapes or without tapes, as determined at random. Frequent quizzes will
determine the number of words actually learned, as opposed to the number that
were studied. At the end of the experiment, we will compute a sample mean (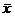 ) by the technique demonstrated below: ) by the technique demonstrated below:
Subject #1 (Aaron Anderson): 83 words learned with tapes, 78 words learned
without tapes, difference = 5.
Subject #2 (Bill Benson): 66 words learned with tapes, 67 words learned
without tapes, difference = –1.
Subject #3 (Cal Clemson): 91 words learned with tapes, 91 words learned
without tapes, difference = 0.
In the example, we would add up 5, –1, and 0, and then we would divide by 3,
since there are 3 students. We would obtain a statistic of 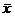 = 1.333. In other words, = 1.333. In other words, 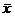 = mean difference per student. = mean difference per student.
If 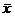 = 0, which is extremely unlikely, we would have seen no
difference with the tapes. If = 0, which is extremely unlikely, we would have seen no
difference with the tapes. If 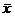 is nonzero, which is
virtually certain, we must analyze the H0
sampling distribution of is nonzero, which is
virtually certain, we must analyze the H0
sampling distribution of 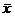 to see if the
difference observed is statistically significant. to see if the
difference observed is statistically significant.
[Note: This experiment does not
have to be done as matched pairs; a fully randomized design would also work
well. In fact, a fully randomized design would probably reduce the placebo
and Hawthorne effects, since students would not be constantly switching
between using tapes and not using tapes. The problem setup required matched
pairs, which is why we used matched pairs. In class, we will discuss the
tradeoffs between the two approaches in detail.]
3. Does cell phone usage while driving increase the mean number of annual
deaths in traffic accidents?
4. Does Axe® deodorant body spray increase the probability that
male users are perceived by females to be desirable? (Warning: Do not try to
replicate the conditions in this commercial.)
5. (Matched pairs.) Does consuming Red Bull immediately before class increase
the probability of passing a STAtistics quiz?
|
|
|
T 2/12/08
|
HW due: Read pp. 540-549; write #10.39.
|
|
|
W 2/13/08
|
HW due: Read pp. 550-553; write #10.40, 10.43.
|
|
|
Th 2/14/08
|
Que (not
quite a “quest”) (20 pts.) on all recent
material. To help you prepare, I am posting solutions to #10.40 and #10.43
below. Please pay careful attention to the amount of work required.
10.40.(a)
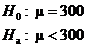
(b)
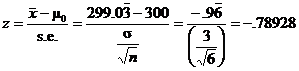
(c)
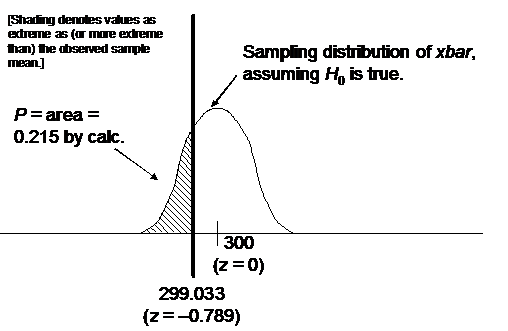
P = 0.215 means that the observed sample mean is not
exactly rare. This is not convincing evidence that the mean contents of cola
bottles is less than 300 ml, since even if the true mean were 300 ml, chance alone would produce a sample mean less than
or equal to 299.033 about 21.5% of the time.
10.43.
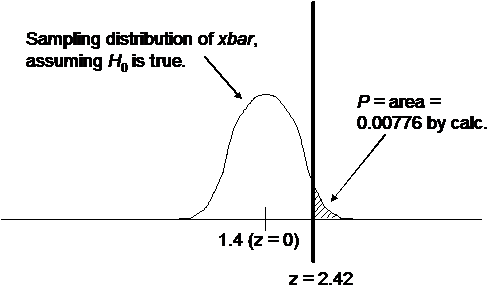
(a) Since the P-value is 0.00776, which is less than 0.05, the result is
significant at the 5% level.
(b) Since the P-value is 0.00776,
which is less than 0.01, the result is also significant at the 1% level.
Alternate answers to 10.43:
(a) Since z = 2.42 > 1.645,
where 1.645 = z* for .05
significance, the result is significant at the 5% level.
(b) Since z = 2.42 > 2.326,
where 2.326 = z* for .01
significance, the result is significant at the 1% level.
Note: The values 1.645 and 2.326
are found (by inspection) in the appropriate columns of Table C. Look near
the bottom, in the row labeled z*.
On the AP exam, this row is labeled 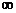 instead of z*. Do you know why? (The reason is
that a t distribution with
infinitely many degrees of freedom, df = instead of z*. Do you know why? (The reason is
that a t distribution with
infinitely many degrees of freedom, df = 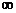 , is another name for the z distribution.) , is another name for the z distribution.)
|
|
|
F 2/15/08
|
No school (faculty
professional day).
|
|
|
M 2/18/08
|
No school (holiday).
|
|
|
T 2/19/08
|
HW due: Reread
the 2/11 calendar entry and the material provided below. I have added
important notes and other information for you to read. No written HW is due.
Enjoy your long weekend, and get plenty of sleep!
Quiz (10 pts.) is likely on the
same material that was covered on last Thursday’s “que.” You will not have
all period to complete it, however. Timing will be similar to that on the AP
exam: slightly more than 2 minutes per question. A sample is provided below.
Example question: Cough drops are manufactured by a machine that is
adjusted to produce a mean output mass of 8 g. If the distribution is normal
and the standard deviation is known to be 0.5 g, compute (1) the proportion
of cough drops that are more than 1.2 g “out of spec” (i.e., more than 1.2 g
away from the nominal mass of 8 g) and (2) the probability that a random
sample of 5 cough drops would have a mean mass that is more than 1.2 g out of
spec. Then (3) state what it would mean to find a random sample of 5 cough
drops with a mean mass this extreme.
Solutions:
(1) Draw a sketch of a normal curve centered on 8. Shade the left tail from 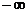 to 6.8 and the right
tail from 9.2 to to 6.8 and the right
tail from 9.2 to 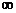 . By calc., the sum of the two areas is 0.0164. . By calc., the sum of the two areas is 0.0164.
(2) Since the distribution is given to be normal with 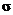 = 0.5, the s.e.
(namely, the s.d. of the sampling distribution of = 0.5, the s.e.
(namely, the s.d. of the sampling distribution of 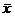 ) is ) is 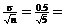 0.2236. Repeat the
operation in (1) by pressing 2nd ENTER on your calculator and changing the fourth
parameter in your normalcdf expression from 5 to 0.2236. Be sure to include
both the left tail and the right tail. Answer: 0.0000000804. 0.2236. Repeat the
operation in (1) by pressing 2nd ENTER on your calculator and changing the fourth
parameter in your normalcdf expression from 5 to 0.2236. Be sure to include
both the left tail and the right tail. Answer: 0.0000000804.
(3) Although individual cough drops with masses less than or equal to 6.8 g
or greater than or equal to 9.2 g do occur about 1.6% of the time, it is
extremely rare for random samples of size 5 to have a mean mass this extreme
(less than one time in 10 million). Therefore, if we were to observe such a
mean in a random sample of size 5, we would conclude that something other
than chance is responsible. Most likely, the machine that makes the cough
drops needs to be readjusted.
Note: A very common student error
is to say in (3) that the probability that chance alone is responsible is
0.0000000804. No! No! No! There is no way to compute the probability that
chance alone is responsible. (Either it is, or it isn’t. Mere mortals are not
able to know that answer based on statistics alone.) What we can say, correctly, is that the P-value of a two-sided z test is 0.0000000804. Remember, a P-value is a conditional probability.
Saying that P = 0.0000000804 means
that the probability of a mean result 6.8 or lower, or 9.2 or higher, given
that the null hypothesis is true, is 0.0000000804. In this problem, H0 is the claim that 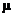 = 8. Because the P-value is low, we would reject H0 in favor of the
two-sided alternative, namely H0: = 8. Because the P-value is low, we would reject H0 in favor of the
two-sided alternative, namely H0:
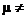 8. 8.
|
|
|
W 2/20/08
|
Quiz (ungraded) will begin the period. No additional reading assignment or problems are
due. However, you will want to reread yesterday’s calendar entry.
For the record, please notice that yesterday’s quiz (if you replace the words
“Jack’s lax team” with “a cough drop machine” and the words “mean of 55 goals
per season” with “mean output mass of 8 g”) was virtually identical to the
sample problem posed in yesterday’s calendar entry. I am not trying to be
tricky, simply trying to make sure that everyone gets to a competency level.
|
|
|
Th 2/21/08
|
Quiz (10 pts.) virtually identical to yesterday’s quiz. I sincerely hope that
yesterday’s quiz was educational and beneficial. If (by your scores today)
you demonstrate that such was the case, I will be happy to schedule more
ungraded quizzes in the future.
HW due: Read pp. 554-562,
especially the summary on p. 556; write #10.48, 10.56.
|
|
|
F 2/22/08
|
HW due:
Read pp. 562-579.
Since today’s class was wiped out by the snow day, you will have to serve as
your own teacher. Spend approximately 50 minutes peppering yourself with questions
and preparing for next Tuesday’s test. By now you should have a feel for the
kinds of questions that I think are especially important (e.g., #10.84,
10.85, 10.86).
|
|
|
M 2/25/08
|
HW due:
Read pp. 579-580; write #10.77, 10.79-82 all, 10.84-86 all. Because of the
time lost to snow, a 35-minute time log is inadequate for today’s assignment.
It is reasonable to expect at least 85 minutes of work, perhaps somewhat more
if you wish to do well on tomorrow’s test.
In class: review.
|
|
|
T 2/26/08
|
Test (100 pts.) on Chapters 9 and 10.
There will be no detailed computation of power on this test. However, you
must know the basics: that power equals (1 – P(Type II error)) and that, if all other aspects of a test remain
unchanged, there is a tradeoff between Type I and Type II error. In other
words, we can decrease the probability of Type I error by lowering the 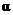 threshold, but in so
doing, we will increase the probability of Type II error. We can decrease the
probability of Type II error (using a more “powerful” or “sensitive” test),
but in so doing, we will increase the probability of Type I error (false
positive). threshold, but in so
doing, we will increase the probability of Type II error. We can decrease the
probability of Type II error (using a more “powerful” or “sensitive” test),
but in so doing, we will increase the probability of Type I error (false
positive).
Increasing the sample size increases power for two reasons, both of which are
consequences of reducing the s.e. and making the sampling distributions
narrower: (1) less of an alternative sampling distribution will bleed far
away from the alternative parameter value, and (2) since the “do not reject H0” boundaries themselves
will move closer to the center of the H0
sampling distribution, values from the Ha
sampling distribution must be more extremely off center in order to reach the
updated “do not reject H0”
boundaries.
Increasing the sample size, if everything else about a test remains
unchanged, will also reduce the m.o.e., which is a good thing. Reason: m.o.e.
is a multiple of s.e., and s.e. is always negatively related to sample size.
We have discussed this “inverse-square-root” relationship several times this
year. To reduce the s.e. and hence the m.o.e. by a factor of, say, 15, you
must increase the sample size by a factor of 152, or 225. (This
can be expensive in real life.)
If your study time is limited, be sure to reread the section and chapter
summaries, and work several odd-numbered problems from each chapter.
You know that certain terms are highly likely to be on the test: m.o.e.,
confidence level, confidence interval, statistical significance, and P-value. There may be penalty points
for anyone who still thinks that a P-value
gives the probability that chance alone has caused an observed effect. Doh!
|
|
|
W 2/27/08
|
HW due:
Reread the material on Type I and Type II error (pp. 567-574) and the
warnings concerning what we called “witch hunts” (pp. 565-566). Prepare
several good questions to ask concerning this material.
|
|
|
Th 2/28/08
|
HW due:
Read pp. 587-589 plus the box on p. 606; write #10.72.
|
|
|
F 2/29/08
|
A rare homework vacation to
celebrate Leap Year! No additional HW is due today, but be sure you are caught
up on all previously assigned material.
|
|