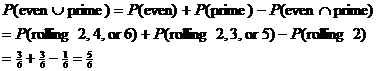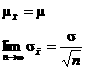|
M 1/7/08
|
HW due: Prepare for your midterm examination, and be
prepared to present oral and/or written evidence (in a 1-minute personal interview)
that you have undertaken some organized form of study. For example, a logbook
showing the problems you have worked in an AP review book would suffice. Your
textbook is also a large source of practice problems.
The material to be covered on the midterm examination includes everything
discussed in class and everything in the textbook through Chapter 8. For more
ideas, please see the 1/15/08 calendar entry.
|
|
|
T 1/8/08
|
Instant
Feedback Quiz. Fair game is
everything covered so far this year. For today’s quiz, it would be reasonable
to expect at least one question on conditional and marginal probabilities in
addition to the usual suspects.
Remember: The following formulas
are always true for events A and B.
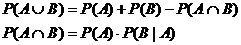
If you know something more about A
and B, the formulas can sometimes be simplified.
For example, if A and B are mutually exclusive, then by
definition their intersection is null. Therefore, the first formula above
could be simplified to say that the probability of A or B happening is the
sum of the probabilities. Students sometimes get confused, perhaps because
when they first learned about probability back in elementary school, “or”
seemed to involve adding things up. Remember, the “adding in a union” concept
is valid only if the events are mutually exclusive. MEAU (mutually exclusive
adds in a union) is the mnemonic.
By the same token, if A and B are independent, then by definition 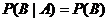 , which means that the second formula above could be
simplified to say that the probability of A
and B both happening is the product
of the probabilities. Students sometimes get confused, perhaps because when
they first learned about probability back in elementary school, “and” seemed
to involve multiplying things. Remember, the “multiplying in an intersection”
concept is valid only if the events are independent. IMI (independent
multiplies in an intersection) is the mnemonic. , which means that the second formula above could be
simplified to say that the probability of A
and B both happening is the product
of the probabilities. Students sometimes get confused, perhaps because when
they first learned about probability back in elementary school, “and” seemed
to involve multiplying things. Remember, the “multiplying in an intersection”
concept is valid only if the events are independent. IMI (independent
multiplies in an intersection) is the mnemonic.
Does one have to memorize the two formulas? Not really. The first is on your
formula sheet, and the second is also on your formula sheet, though in the
slightly disguised version shown below:
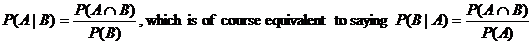
Example: Compute the probability
of getting an even number or a prime number when rolling a die.
Solution:
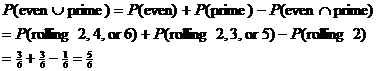
Example: Compute the probability
of drawing an ace first, followed by either an ace or a jack (without
replacement).
Solution:
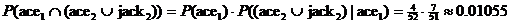
|
|
|
W 1/9/08
|
Instant Feedback Quiz.
Answer key with explanations:
1. C. If choice A had said “predicted value of the response variable,” then E
would be correct.
2. A. Joint probabilities are probabilities of intersections. Marginal
probabilities are unconditional probabilities, e.g., P(left-handed) or P(large
shoe). You can verify by multiplying that in each case 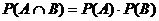 , but that takes a long time. Easier is to notice that
since the ratios are the same in each row (namely, 1:4), the category
split-outs must not be affecting the probabilities. Therefore, shoe size and
handedness are independent. Choice B is a distractor, since it is a common
student error to confuse joint and conditional probabilities. , but that takes a long time. Easier is to notice that
since the ratios are the same in each row (namely, 1:4), the category
split-outs must not be affecting the probabilities. Therefore, shoe size and
handedness are independent. Choice B is a distractor, since it is a common
student error to confuse joint and conditional probabilities.
3. D. Willie’s question immediately before the quiz was right on target!
4. A. If Q1 denotes the
25th percentile and Q3
denotes the 75th percentile, then Q2
would denote the median. Remember, left skewness will pull the mean low, and
right skewness will pull the mean high, but the median is resistant.
|
|
|
Th 1/10/08
|
Instant
Feedback Quiz.
|
|
|
F 1/11/08
|
Instant
Feedback Quiz.
Optional HW due: If you submit a
well-written short essay on the subject of the definition, purpose, and advantages
of the Monte Carlo method (a.k.a. simulation), you can win back not only the points
you lost on question #4 of yesterday’s quiz, but 5 additional points. If you
did fairly well on the quiz yesterday, this HW can be treated as a bonus.
You may consult your textbook, other printed resources, and even the
Wikipedia article if you wish. However, the words you write must be your own.
Suggested length is 5-7 sentences or 1-2 paragraphs.
Here is yesterday’s quiz, along with solutions. A number of people did very
poorly on this quiz. Please learn from your mistakes, so that if some of the
questions were recycled in the future, you would be able to do better.
Instant Feedback Quiz III
1. A fair coin is flipped 482 times. Compute the probability of getting at
least 246 heads. Give answer to 7 decimal places.
2. In a coin-flipping situation such as #1, compute the probability that the
first head occurs strictly before the third flip.
3. If a Mr. Hansen midterm exam follows the N(77, 10) distribution, compute the probability that a randomly
selected paper is in the B range (i.e., score 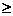 80 but strictly <90). Fractional points are permitted. 80 but strictly <90). Fractional points are permitted.
4. The Monte Carlo method is a synonym for s___________n.
Solutions:
1. Distribution is B(482, 0.5) if X denotes # of heads in 482 flips.
Therefore, P(X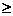 246) = 1 – P(X < 246) = 1 – 0.65905288 = 0.3409471
by calc. 246) = 1 – P(X < 246) = 1 – 0.65905288 = 0.3409471
by calc.
2. If Y denotes # of flips needed
to obtain first head, then Y is
geometric with p = 0.5. Therefore, P(Y
< 3) = P(Y = 1) + P(Y = 2) = 0.75 by calc. Keystrokes
(which you cannot show) would be geometpdf(.5,1)+geometpdf(.5,2) or, if you
prefer a slightly faster method, geometcdf(.5,2). You can also use regular
probability: P(Y = 1) = P(head on the
very first try) = 0.5, and P(Y = 2) = P(tail1 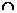 head2) =
(0.5)2 = 0.25. Since these are mutually exclusive, add to get the
answer of 0.75. head2) =
(0.5)2 = 0.25. Since these are mutually exclusive, add to get the
answer of 0.75.
3. With continuous distributions (and all normal distributions are
continuous), the inclusion or exclusion of endpoints is irrelevant.
Calculator keystrokes, which you cannot show, would be normalcdf(80,90,77,10)
to give an answer of 0.285. If work had been required, you would show
a sketch of a normal curve with mean 77 and s.d. of 10, with the area from 80
to 90 shaded.
4. imulatio
|
|
|
T 1/15/08
|
Midterm Exam, 8:00 a.m., LJ-300 (Mathplex South). This is a change from the original schedule. The revised
schedule for all exams is available here.
The format of the exam will resemble a scaled-down AP exam.
On the actual AP exam, you must
answer 40 multiple-choice questions in 90 minutes, then 6 multi-part
free-response questions in 90 minutes. The free-response questions are “5
shorts and a long”—in other words, 5 fairly straightforward questions for
which you should budget about 13 minutes each, and a longer “project-type”
question for which you should budget about 25 minutes. The long question may
involve, for example, a simulation, a curve-fitting and data interpretation
exercise, or an extended experimental design with variations.
On your midterm exam, the format
will be scaled down as follows:
Multiple choice: 16 questions in 36 minutes.
Free response “short”: 2 questions in 26 minutes.
Free response “long”: 1 question in 25 minutes.
That gives a total running time of 87 minutes (130.5 for extended-time
students). Because this is your first experience with the AP format, I will
let you have a little more time if you need it, and I will not collect the
multiple-choice part after 36 minutes. However, please remember that on the
real AP exam, the multiple-choice and free-response portions are separate,
and you will have to stop working on multiple-choice questions at the halfway
point even if you have not finished them.
A graphing calculator is required. A spare calculator and/or spare batteries
are strongly recommended, since (as during the actual AP exam) no help will
be provided if your calculator malfunctions or conks out.
Because you will be provided with the exact formulas and tables found on pp.
11-17 of the AP
course description, there is little to be gained by memorizing formulas.
There are only two formulas that I consider to be worth memorizing: 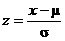 and and 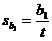 , ,
neither of which appears on your formula sheet. (The second of these is used
only in the second semester and is thus irrelevant to the midterm exam.)
However, you are supposed to know certain key facts that may require
memorization, depending on how nimble your brain is. For example, some
students already know the 68-95-99.7 rule (a.k.a. the empirical rule for
normal distributions) without studying, but others will need to memorize it
anew. Other examples of key facts are that the LSRL residuals always add up
to 0 and that the LSRL itself always passes through 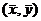 . These are supposed to be part of your DNA by now, but if
not, you will have to memorize them. Other key facts can be found in the
handy chapter summaries that your textbook has provided for you. . These are supposed to be part of your DNA by now, but if
not, you will have to memorize them. Other key facts can be found in the
handy chapter summaries that your textbook has provided for you.
Believe it or not, two places where I have consistently observed students
losing a frightening number of points are terminology
and notation. These two categories
should be freebies! (Or so one would think.) And I am not simply talking
about failure to cross the z,
although I will deduct for that. I am talking about students who do not know
what expected value means, students who do not know what a random variable is
or how to declare one coherently, students whose probability notation is
completely indecipherable, students who think “mutually exclusive” and
“independent” are synonyms, students who think “regression outlier” and
“influential observation” are synonyms, and students who cannot tell the
difference between joint, conditional, and marginal probability—or if they
do, they have no way to communicate that knowledge, since their notation is
nonstandard or nonexistent. The list goes on and on. Basically, here are the
reasons that the AP (and I as well) place such emphasis on terminology and
notation:
1. Computers
handle the number crunching for us nowadays.
2. Therefore,
the only way we can possibly consider ourselves educated in the subject of
statistics is if we understand the terminology and notation with the
competence that someone in the field of statistics would have to have.
The best way to practice for the endurance required would be to take one or
more actual exams from your AP exam book. Simply ignore the
problems—approximately half—that deal with confidence intervals, P values, chi-square, t values, t scores in LSRL slopes, and other second-semester topics. (Of
course, garden-variety LSRL problems, probability problems, binomial and
geometric random variables, experimental design, etc. are all fair game. If
you find yourself omitting questions from these categories, you know you are
not yet ready to take the midterm.)
|
|
|
M 1/21/08
|
No school (holiday).
|
|
|
T 1/22/08
|
No school (faculty meetings). If you did not receive
an e-mail message with your quarter and semester grades, please contact me.
|
|
|
W 1/23/08
|
Start of second semester.
|
|
|
Th 1/24/08
|
HW due: Read pp. 456-467. A quiz is likely. Question 1: What is the central theme of the
second semester? Question 2: What is the central abstract concept involved in
addressing Question 1?
|
|
|
F 1/25/08
|
HW due: Read pp. 472-477 plus the summaries on p. 469 and
p. 479; write #9.11. Note that there is a typographical error in part (e) of
#9.11. The first sentence should say, “. . . the 10 results for sample size =
100 in list L3.”
Quiz (10 pts.) will cover the
rules of thumb found on p. 473 and p. 475. You will be given a formula sheet
(downloadable as pp. 11-12 from the College Board at this
link), and you will be asked to compute the mean and standard deviation
of 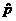 under various sets
of assumptions. Some examples are given below. under various sets
of assumptions. Some examples are given below.
1. Suppose that the true fraction of Northern Virginia Nimrods (total
membership, 300 people) that hate wearing mittens is 45%. For an SRS of 100
members of this club, compute the mean and standard deviation of the sampling
distribution of 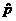 . Use accurate language to state what these signify. . Use accurate language to state what these signify.
Solution: The mean of 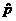 is given by is given by 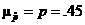 , which signifies the expected proportion of Northern
Virginia Nimrods in the SRS who hate wearing mittens. The standard deviation
of , which signifies the expected proportion of Northern
Virginia Nimrods in the SRS who hate wearing mittens. The standard deviation
of 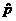 cannot reliably be
computed by formula, since 100 represents more than a tenth of the population
of the club. (Remember, the formula assumes a binomial distribution, which we do not have since independence is
violated.) The meaning of cannot reliably be
computed by formula, since 100 represents more than a tenth of the population
of the club. (Remember, the formula assumes a binomial distribution, which we do not have since independence is
violated.) The meaning of 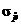 is the standard
deviation of the imaginary (hypothetical) distribution formed by computing
all possible is the standard
deviation of the imaginary (hypothetical) distribution formed by computing
all possible 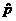 values when a
100-person SRS is polled from the Northern Virginia Nimrods. values when a
100-person SRS is polled from the Northern Virginia Nimrods.
2. Suppose (omnisciently) that 45% of St. Albans Upper School students hate
mittens. If a 30-person SRS of St. Albans Upper School students is polled on
this question for an Independent
survey, compute the mean and standard deviation of the sampling distribution
of 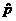 . Assume that response bias, nonresponse bias, tabulation
bias, and all other potential sources of error are negligible, so that the issue
of sampling error is the only relevant one to consider. . Assume that response bias, nonresponse bias, tabulation
bias, and all other potential sources of error are negligible, so that the issue
of sampling error is the only relevant one to consider.
Solution: As above, the mean of 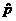 is given by is given by 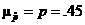 . However, since the population (314 students) is more than
10 times larger than n = 30, and
since np = 30(.45) = 13.5 and nq = 30(.55) = 16.5 are both at least
10, we can use the binomial formula . However, since the population (314 students) is more than
10 times larger than n = 30, and
since np = 30(.45) = 13.5 and nq = 30(.55) = 16.5 are both at least
10, we can use the binomial formula 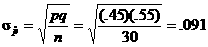
as a reasonable estimate of the standard deviation of the sampling
distribution.
Footnote
to #2: Most school newspaper polls are made using a convenience
sample instead of an SRS, making them, as you know, essentially worthless.
However, even if a proper SRS of 30 students is polled, the standard
deviation of the sampling distribution of 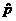 was computed above
to be .091, which is large. Since we know by the Empirical Rule that the
central 68% of a normal distribution (and this one is approximately normal)
is contained within was computed above
to be .091, which is large. Since we know by the Empirical Rule that the
central 68% of a normal distribution (and this one is approximately normal)
is contained within 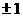 standard deviation
of the mean, we would have only 68% confidence that our poll’s outcome is
within 9.1 percentage points of the true parameter. To get 95% confidence,
which is the standard for most published polls, we would have to go out to
about 1.96 standard deviations, thus obtaining a whopping 17.8% m.o.e.!
(Computational details: 1.96 times the .091 that we obtained above equals
.178.) standard deviation
of the mean, we would have only 68% confidence that our poll’s outcome is
within 9.1 percentage points of the true parameter. To get 95% confidence,
which is the standard for most published polls, we would have to go out to
about 1.96 standard deviations, thus obtaining a whopping 17.8% m.o.e.!
(Computational details: 1.96 times the .091 that we obtained above equals
.178.)
At any rate, imagine that the poll is conducted, and 11 out of the 30 people
polled say they hate mittens, which is certainly plausible. Imagine how this
would look: “Independent survey
finds that 36.667% of Upper Schoolers, plus or minus 17.8%, hate wearing
mittens.” The survey would be dismissed as fluff, one would hope, since the
margin of error is absurdly large. All we can say with confidence is that
somewhere between 19% and 54% of the Upper Schoolers hate wearing mittens,
but that is such a wide spread that it should not be of any interest to
anyone.
Moral of the story: When printing polls, you need to avoid having a story
that is irrelevant. Unfortunately, many student journalists, and even some
professional ones, take a shortcut. They may either use a convenience sample,
in which case the poll is worthless since no m.o.e. can be computed, or they
may use an SRS and fail to report the absurdly large m.o.e. To get a small
m.o.e. (say, 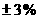 ) with a high confidence level (95% is the usual standard)
requires a sample size of more than 1,000 if the population is large. (You
may be able to compute this already. We will study the technique in more
detail later in the course.) In a population of 314, the sample size would
have to be about 240, based on techniques that we will not study in our
class. ) with a high confidence level (95% is the usual standard)
requires a sample size of more than 1,000 if the population is large. (You
may be able to compute this already. We will study the technique in more
detail later in the course.) In a population of 314, the sample size would
have to be about 240, based on techniques that we will not study in our
class.
|
|
|
M 1/28/08
|
HW due: Read pp. 481-497 and implement the correction
described below. You may skip over the exercises for now, but be sure to read
all examples, especially Example 9.8.
Error correction: On p. 489, in the
fourth line of text, change the word “taking” to “approaching.” The sentence
should then read as follows:
The mean remains at 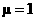 and the standard
deviation decreases, approaching the value and the standard
deviation decreases, approaching the value 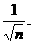
The mathematical symbol for “approaches” is a single arrow pointing to the
right: 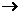 . .
The reason the error correction above is needed is that the CLT guarantees
that as 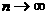 , the sampling distribution of , the sampling distribution of 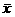 becomes more and
more like becomes more and
more like 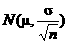 . In “precal-like” notation, we have the following: . In “precal-like” notation, we have the following:
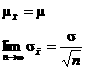
The CLT does not say that 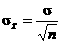 ; CLT says that ; CLT says that 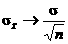 as as 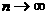 . .
After all, it is called the Central Limit Theorem for a reason. It is not
called the Central “Equals” Theorem! Note:
Use of the equal sign for the standard deviation of 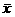 is correct if the
underlying data distribution is normal. However, that almost never occurs in
real-world problems. Except for the occasional trick question, you are much
safer on the AP remembering that the standard deviation of is correct if the
underlying data distribution is normal. However, that almost never occurs in
real-world problems. Except for the occasional trick question, you are much
safer on the AP remembering that the standard deviation of 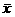 approaches the expression in the formula as approaches the expression in the formula as 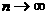 . .
|
|
|
T 1/29/08
|
HW due: Play with the sampling
distribution simulation that we looked at in class yesterday. Be prepared
to make accurate predictions about what will happen, just as I was asking you
questions during the demonstration yesterday. Note: Remember that N
in the window should actually be n.
|
|
|
W 1/30/08
|
HW due: Write #9.41-9.46 all. Use the odd-numbered
questions as a “lever” to help you understand and work the even-numbered
questions. Note, however, that the book’s odd-numbered answers (which you are
encouraged to check) do not constitute adequate work. For example, here is
how you should respond to #9.43(b):
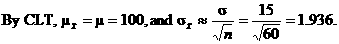
If you merely copy the book’s abbreviated answer, you will have not shown
enough work to indicate that you understand the notation and formulas taught
in this chapter.
|
|
|
Th 1/31/08
|
HW due: Write #9.47, correct your work from yesterday’s
assignment, and perform the following two simple exercises.
Exercise 1: Mark this clearly on
your paper as “Exercise 1.” Write a collection of 0’s and 1’s, 50 of them in
all, divided off in groups of 5. Make them as random as you can without using
a calculator, a coin, or any other tools. Here is what your set might look
like:
00101 | 11000 | 01101 | 00110 | 10110 | 00100 | 11010 | 00101 | 01101 | 10010
Exercise 2: Mark this clearly on
your paper as “Exercise 2.” Create a second collection of 0’s and 1’s, as
before, but made with the help of a coin or a random integer generator on
your calculator. Here is my set, but you may not copy my work:
00100 | 00001 | 11111 | 11111 | 00000 | 00001 | 01001 | 00001 | 11000 | 10100
In keeping with Mr. Kelley’s admonition that one should never work
probability problems without having the answers, here are the answers to the
even-numbered problems.
9.42(a) 3525 (b) 0.6752
9.44 0.95368
9.46(a) mean = 50, s.d. = 6.3246 (b) 0.0569
|
|