|
M 12/3/07
|
HW due:
1. If your initials are MA, you still need to submit question #17. If your
initials are CK, WM, LS, AW, or JZ, you need to submit all of Friday’s data.
Be sure to put a double underscore ( __ ) at the beginning of your subject
line. If your initials are AB, then I assumed that your “D” entries were
actually supposed to be the letter “O,” and you do not need to resubmit.
2. On p. 369, near the top of the page, use a pen to change the first
sentence as follows:
Original version: A discrete random
variable X has a countable
number of possible values.
Corrected version: A discrete random
variable X has possible values
that are all separated by gaps. In most cases, these possible values will be
integers. However, they could also be decimal values (such as 98.6, 98.7,
98.8, . . .) that are separated by gaps between the possible values.
In other words, you will be crossing out the words “a countable number of”
and inserting a bit more than 2 sentences.
Please see me if you would like a thorough explanation of the need for this
change. Basically, your textbook is simply incorrect in its definition.
3. Read pp. 367-377.
4. Read the following concerning the memory aids DOGS and COIN. If they help
you, so much the better.
DOGS: Discrete random
variables have Outcomes
that are Gap-Separated.
COIN: Continuous random
variables have Outcomes
that cover an entire Interval
of Numbers.
For example, the dollar value of money in my pocket on a randomly selected
day would be a discrete random variable since there is always a gap between
possible values (such as $1.68 and $1.69). It is not possible to have
$1.6883572 in my pocket, or an irrational number of dollars, for that matter.
The maximum egg-splat diameter when a randomly chosen egg crashes on the
stones beneath the Lower School is a continuous random variable, since
(theoretically) any value between 0 inches and about 50 inches is possible.
There are no gaps.
|
|
|
T 12/4/07
|
HW due: Read pp. 377-380; write #7.8, 7.10, and the
following simulation:
The anecdotal data I have gathered suggest that many of you think Charlie
will win money from me (see 11/30 calendar entry) or at worst have a fair
bet. However, I assure you that the odds are on my side. Write out a
simulation procedure to estimate how much money I will be ahead after we play
10 rounds. Perform at least 3 replications (i.e., 3 trials of 10 rounds each)
and average your results.
Finally, LS and JZ still need to submit their e-mail that was due on 11/30.
|
|
|
W 12/5/07
|
HW due: Read pp. 385-394 and make sure all previous written
work is up to date.
Also, JZ still needs to submit the e-mail that was due on 11/30. LS, WM, and
several other students drove me slightly crazy (I know, short drive) by
failing to observe the required format and/or omitting data, but I have now
finished compiling almost all the data.
|
|
|
Th 12/6/07
|
HW due: Read pp. 395-406. Read all examples, especially
Example 7.13 on p. 402. (You may omit the exercises for now.)
Also, if time permits, please send some anonymous e-mail feedback by clicking
here.
Important: When asked, please type
Stu Dent as your name and stat [at sign] modd.net as your address so that I
cannot tell who you are. If you enter a truly phony e-mail address such as
stat [at sign] stuvwxy.com, the message will not be delivered—it will simply go into the bit bucket and nobody
will ever see it again. You must use a plausible address for a real website,
such as modd.net, so that the message will be delivered to me.
What do you enjoy about our class? What do you dislike? Are teaching aids
(chalkboard, website, etc.) being used effectively? Are you learning? Are you
bored? What you would you like to tell Mr. Hansen to do differently—or do
more of? These are the kinds of things I want to know about.
|
|
|
F 12/7/07
|
HW due: Write #7.34, 7.35, 7.36.
|
|
|
M 12/10/07
|
No additional written work due. Use this time to get
caught up on older assignments, or work ahead on tomorrow’s assignment.
|
|
|
T 12/11/07
|
HW due: A priori probability problems.
|
|
|
W 12/12/07
|
HW due:
1. Complete your problem set that was due yesterday. For any problems that
you are not certain of, I would expect you to perform a simulation to at
least determine whether your answer is “in the ballpark” or not. Please, no
way-off guesses!
2. Show by means of analytic (a priori)
proof that if 5 cards are drawn (without replacement) from a well-shuffled
deck, and if X is a random variable
representing the number of aces obtained, then
P(X = 0) = 0.658842
P(X = 1) = 0.299474
P(X = 2) = 0.039930
P(X = 3) = 0.001736
P(X = 4) = 0.000018
P(X 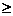 5) = 0 5) = 0
3. Use the results of #2 to compute  . Show your work for both. If you do your work well, I will
not ask you to show your work on the test. (If you do not do this well, you
will be required to show your work on the test in order to earn credit for
this type of problem.) . Show your work for both. If you do your work well, I will
not ask you to show your work on the test. (If you do not do this well, you
will be required to show your work on the test in order to earn credit for
this type of problem.)
Important note: You can do #3 even
if you cannot do #2, since everything you need as raw material is provided
for you. All you need is the probability of each outcome and the value of the
random variable so obtained.
|
|
|
Th 12/13/07
|
HW due: Write #7.42, 7.44, and the following question.
Compute any 2 or more of the following probabilities, showing your work. For
each draw, assume that 5 cards are selected without replacement from a
well-shuffled deck. Note that I consider “royal flush” to be a special case
of straight flush, not something to compute separately. The term “full house”
refers to 3 cards of one denomination and 2 of another denomination. We did
the straight flush in class, and you may use it as one of your 2 problems if
you wish.
P(straight flush) = 40/52C5 = 0.00001539
P(four of a kind)
P(full house)
P(flush)
P(straight)
P(three of a kind)
P(two pair)
P(one pair)
P(junk)
In class: Review.
|
|
|
F 12/14/07
|
Test (100
pts.) on all recent probability and
random variable material through p. 406. Note that the terms influential observation and regression outlier may also be tested,
along with terminology such as 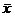 (sample mean) and (sample mean) and 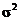 (population
variance) that we use all year. (population
variance) that we use all year.
|
|
|
M 12/17/07
|
Makeup
Test (100 pts.) for Lawton,
Michael, and Willie, 7:00 a.m., Mathplex South.
HW due: Read pp. 414-433. You may
omit Activity 8 on pp. 414-415 and the exercises, but do read the
introduction on p. 414 and all 12 of the examples. I think one of the reasons
that some students have been having trouble is that they may be skipping over
the examples or skipping the textbook readings altogether. Examples are not
“fluff”: They are integral to your understanding of the material. It is
always astonishing to me that students view textbook content as something to
be skipped over, but if I distribute the same type of material repackaged as
a “test study guide” (or better yet, as a “sample test with explanations”),
they eat it up.
Quiz (10 pts.) on the reading
assignment is possible. This would be an open-notes quiz.
|
|
|
T 12/18/07
|
HW due: Read pp. 434-444; write #8.22 and the following
problem.
If the height (in inches) of STA students is distributed according to N(71, 4) and the height of NCS
students follows N(67, 2.5),
compute the probability that a randomly chosen STA student going to a dance
is taller than his randomly chosen NCS date. Hint: Let S = r . v.
for height of STA student, T = r.
v. for height of NCS student, and compute P(S – T > 0). You may assume that Z = S – T is also normally distributed.
|
|
|
W 12/19/07
|
HW due: Read pp. 446-447; write #8.38, 8.44.
|
|
|
Th 12/20/07
|
Quiz (10
pts.) is likely on binomial and
geometric calculations (binompdf, binomcdf, geometpdf, geometcdf). Example
problems abound in your textbook. No additional written work is due. Here are
the answers to #8.38 and 8.44:
8.38(a) Yes. [You have to check the criteria and state that each is
satisfied.]
(b) 75 [Notation 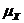 , formula, plug-ins, and answer are required for credit.] , formula, plug-ins, and answer are required for credit.]
(c) 0.2313 [The identifying mark 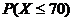 is needed for
credit. Do not write binomcdf.] is needed for
credit. Do not write binomcdf.]
(d) 200 [Work is required for credit.]
8.44(a) 0.325 [Work is minimal, but work is required for credit.]
(b) 0.69245 [Work is required for credit.]
(c) 0.208 [Work is required for credit.]
(d) 3.08 [Work is required for credit.]
(e) [Nothing to show.]
(f) First graph is skew right with first bar of
height 0.325. Second graph has first bar of height 0.325 and then marches
higher and higher, approaching a maximum height of 1.
|
|
|
F 12/21/07
|
Another
Quiz similar to yesterday’s quiz is
possible. No additional written HW is due, so that you can attend the Lessons
and Carols service at the Cathedral.
|
|