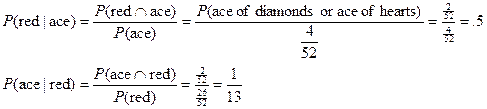A Priori Probability Problem Set

AP Statistics / Mr. Hansen
12/2/2006 [rev. 12/9/2007, 11/4/2016]

Name: _________________________

A Priori Probability Problem Set

Read this paragraph carefully: For most real-world problems of interest, probability should be estimated from real-world data or from a Monte Carlo simulation. However, there is a certain class of problems (including problems seen on the AP exam) that can be solved by means of what is called a priori analysis. The phrase a priori is from Latin and means “relating to or derived by reasoning from self-evident propositions,” to quote Merriam-Webster. Probability estimates based on Monte Carlo simulations or observations of actual experience are called “empirical” or a posteriori.

Recall the basics of a priori probability that you learned both here and in previous classes:

Permutations and combinations (covered in Algebra II and Precalculus)

Mutually exclusive events (events that cannot both occur at the same time)

Independent events (events whose probabilities are not affected in any way by the occurrence or non-occurrence of another event; an example would be successive die rolls, where the die has no memory and keeps a constant P(1), regardless of how many ones may have been rolled previously)

Events and their complements

Counting rules, especially the general multiplication rule

General union rule: is always true, even if A and B are mutually exclusive events. (If A and B are mutually exclusive, the subtracted term is simply 0.)

General intersection rule: is always true, even if A and B are independent events. (If A and B are independent, the factor P(B | A) can be simplified to P(B), since A has no effect on B.)

Conditional probability formula

This problem set will help you reinforce those concepts. Several sample problems are given at the beginning to help you get started. Important: Read all the sample problems. They are educational.

S1.	Compute the number of ways that the letters in the word STATISTICS can be arranged. Use proper notation throughout. Answer: Since there are 10 letters, it would appear that the answer is ₁₀P₁₀ = 10! = 3,628,800. However, these permutations overcount the arrangements of S, T, and I, all of which occur multiple times and should be treated as indistinguishable. For each of the 3! ways that the S’s can be arranged in any pattern, there are 3! ways that the T’s can be arranged, and for each of those, there are 2! ways that the I’s can be arranged. Therefore, if we are not careful, we will overcount by a factor of 3! · 3! · 2! = 72. Final answer: 3,628,800/72 = 50,400.

S2.	In how many ways can an Upper School committee of 12 students be formed if the committee must consist of 2 students from each of the 2 lower forms and 4 students from each of the 2 upper forms? (Upper School class counts are currently 84 in the Class of 2011, 79 in the Class of 2010, 75 in the Class of 2009, and 76 in the Class of 2008, for a total of 314.) Answer: There are 4 separate tasks, namely the “choosing” of students in each form. By the multiplication rule (one of the counting rules), we multiply the number of ways for each form. Final answer: ₈₄C₂ · ₇₉C₂ · ₇₅C₄ · ₇₆C₄ = 16,748,440,428,133,732,500.

S3.	If HIV infection has an incidence of 1.5% in the population of a certain large city, compute the probability that an SRS of 20 people contains at least one person who is HIV-positive. Answer: Naive people might think of multiplying 0.015 by 20 to get .3, but that is clearly invalid. (Reason: By extension of that logic, an SRS of 80 would give a probability of 0.015 · 80 = 1.2, which is obviously impossible.) The correct method is to consider the probability of the complementary event, namely P(nobody is HIV-positive), and subtract from 1. To do this, we compute P(nobody is HIV-positive) = P(person 1 is negative) · P(person 2 is negative \| person 1 is negative) · P(person 3 is negative \| persons 1 and 2 are both negative) · . . . · P(person 20 is negative \| persons 1 through 19 are all negative). The conditional probabilities are required by the general intersection rule. Now, these conditional probabilities are extremely hard to compute. Luckily, in a “large” city, an SRS of 20 people is almost exactly the same process as a series of independent selections, the only difference being that an SRS excludes the possibility that anyone is selected twice. Since the chance of drawing the same person twice in 20 selections from a “large” city is negligible, we allow ourselves the luxury of using the modification of the general intersection rule in which we ignore conditional probabilities. Thus we have 0.985, the probability of a subject’s being HIV-negative, multiplied by itself 20 times, or 0.985²⁰ » 0.739. Final answer: 1 – 0.739 = 0.261.

S4.	Compute the probability of drawing a red card or an ace on a single draw from a well-shuffled deck. Answer: By the general union rule, P(red È ace) = P(red) + P(ace) – P(red Ç ace). Since there are two red aces (namely, the ace of diamonds and the ace of hearts), we have , or approximately 0.538.

S5.	Prove that “red” and “ace” are independent events in a standard deck of cards. Answer: P(red \| ace) = 2/4 since there are 2 red aces out of 4 total aces. The unconditional probability of red, P(red), is 26/52 since half the cards in the deck are red. Because these fractions are equal, “red” and “ace” are independent. (The occurrence or lack of occurrence for each does not affect the probability of the other.) Note 1: You are not required to check that P(ace \| red) = P(ace), but you may do so if you wish. Either check is sufficient to establish independence. P(ace \| red) = 2/26, and the unconditional probability, P(ace) = 4/52, is exactly the same. Note 2: These probabilities were easy enough to do with common sense, and we did not need the conditional probability formula. If you wish to use the formula, here is some practice:

S6.	Prove that “ace” and “face card” are mutually exclusive events. Answer: Mutually exclusive means that the joint probability is 0. Since there are no aces that are face cards (jack, queen, or king), P(ace Ç face) = 0 as required. (Q.E.D.)

	Problems for you to work on your own Important: Show work, notation, and proper explanations. Numeric answers presented “bare” will not qualify for full credit.

1.	Prove that “ace” and “face card” are not independent events.
2.	Compute the number of bridge hands possible (13 cards selected as an SRS from a 52-card deck).
3.	Compute the probability of obtaining 3 hearts and 2 clubs in a randomly dealt 5-card poker hand. (There are 13 hearts and 13 clubs in a standard deck.)
4.	Prove that “2” and “even number” are not independent events when rolling a 6-sided fair die, numbered 1 through 6.
5.	Two fair dice are rolled. Compute the probability of obtaining “boxcars” (double 6).
6.	Two fair dice are rolled twice. Compute the probability of obtaining “boxcars” on at least one of the rolls.
7.	Two fair dice are rolled. Compute the probability of obtaining a sum of 8.
8.	Two fair dice are rolled. Both of them fall on the linoleum floor where you cannot see them. A trusted friend says, “At least one of the dice is a 6.” (Now, clearly this does not always happen. Sometimes there will be no 6’s. However, we are considering a conditional probability situation where at least one 6 is visible to your trusted friend, who always tells the truth.) Given that at least one of the dice is a 6, what is the probability that you have rolled “boxcars”?