|
F 2/1/08
|
No additional HW due
(Thursday is Form V college night). However, make sure all previously
assigned work is up to date.
|
|
|
M 2/4/08
|
HW due (but not to be collected until Tuesday): Read #20 on p. 424; write §8-9 #11, 13, 14, 16, 18,
20c.
Quiz (10 pts.) on recent material
is possible. If it occurs, Form VI students will be allowed to make it up
without penalty at the start of class Tuesday.
|
|
|
T 2/5/08
|
HW due:
Read §9-2; write §8-9 #17ab, 20abdefgh.
|
|
|
W 2/6/08
|
HW due:
Read §9-3; write §9-2 #1-11 all.
|
|
|
Th 2/7/08
|
HW due:
Read §9-4; write §9-3 #3-48 mo3. The objective is to become fast, and that requires doing a number
of problems. After you are proficient, you may wish to do additional
odd-numbered problems for practice. Although rapid repeated integration by
parts is not on the AP exam, the technique is useful to know.
|
|
|
F 2/8/08
|
Test (100 pts.) on all of Chapter 8 except for §8-8.
Remember to bring your binder so that your HW can be checked.
Assignments from the first semester (i.e., before Jan. 23) will not be
checked, nor will Chapter 9 assignments. The following is a complete list of
problems that may be checked:
§8-3 #12, 19
§8-4 #10, 14, 16, 18
§8-5 #1, 2, 6, 8, 11, 26
§8-6 #7 (both by washers and by shells), 8, 16, 20, 23
§8-7 #14, 21, 22
§8-9 #11, 13, 14, 16, 18, 20 (all parts)
Reading notes: §§8-6, 8-7, and 8-9 at minimum.
Format of the test will be free response only. A short “no-calculator”
section (integral setups only) will be followed by a longer section on which
calculators will be required.
Late-breaking change: Supplements
to question #5 on today’s test will be
accepted until 3:30 p.m. this afternoon (Friday). Hand-deliver your paper to
me, or if you accept the small risk, slip it under my office door. Papers
delivered through other means are not safe at all.
|
|
|
Weekend
|
Please relax. There is no need
for an optional re-do of Friday’s test, since almost everyone did fine. (The
mean score was 84, the median was a little higher, and the standard deviation
was about 8. These statistics are completely typical.)
The existing scores will stand. Everyone who took the test should have
already received an e-mail from me with his test score.
|
|
|
M 2/11/08
|
HW due:
Read §9-4 and #20 on p. 450; write §9-4 #13a-18a all. Note that these are application problems. There is no
difficult conceptual work; simply apply the appropriate reduction formulas
from the green box on p. 449. Follow Example 3 on p. 448 for the technique.
Note that after applying the reduction formula once, you will have to apply
the reduction formula additional times on the “reduced” part, as shown in
Example 3.
Optional HW: If you are curious,
you can visit calc101.com or a similar site to do the “b” parts of the
assignment. No password is necessary at calc101.com as long as you are
willing to receive only the answer (no intermediate steps).
|
|
|
T 2/12/08
|
HW due:
Read §9-5; memorize the box at the bottom of p. 452; write §9-5 #3-30 mo3,
35, 36.
If, as Bob suggests, you are able to re-derive the identities on p. 452
quickly from the other identities you are supposed to know already, then you
may be able to skip the memorization.
|
|
|
W 2/13/08
|
HW due:
Read both §9-6 and §9-7. (No additional written work is due today, but make
sure your older problems are up to date.)
|
|
|
Th 2/14/08
|
HW due:
Write §9-7 #3, 9, 11, 12, (13), 15, 19. You may omit #13 if time is short.
|
|
|
F 2/15/08
|
No school (faculty
professional day).
|
|
|
M 2/18/08
|
No school (holiday).
|
|
|
T 2/19/08
|
No additional HW due. Enjoy
your long weekend, and get plenty of sleep!
|
|
|
W 2/20/08
|
HW due (as announced in class): Read §§9-8 and 9-9; write §9-7 #19. We will do a
selection of §9-8 problems in class instead of doing them as HW.
|
|
|
Th 2/21/08
|
HW due:
Read (do not write) §9-9 #23 and 24; then write §9-9 #5, 10, 17, 25abc, 34.
|
|
|
F 2/22/08
|
HW due:
Read §§9-10 and 9-11 (there is no new material in §9-11, only a pair of
review boxes); write §9-10 #1, 3, 17, 19, 20.
Since today’s class was wiped out by the snow day, you will have to be your
own teacher. Let me describe what we would have done if we had had class, and
then you should set aside about 50 minutes to do the same. (Please don’t say
that you have lots of other things you need to be doing on your day off, or
if you do, at least don’t tell me that you need to visit your friends. The
whole point of a snow day is to keep you off the roads.)
First, review the §9-10 homework. The important thing with improper integrals
is to write “lim” over and over again. Use your knowledge of limits to answer
the question.
All of the answers are in the back of the book, except for #20, which is
virtually the same as the odd-numbered problem that precedes it. However,
when we scan HW on Monday, no credit will be provided for answers unless they
are supported by work. Here, for example, is the correct way of doing #1(b):
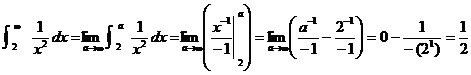
Second, we would do #23 on p. 489. The answers are provided in your book. Do
the setup and computation as part of your assignment for Monday.
Third, we would talk about (but not actually do) #24 on p. 490. This is a
famous problem in mathematics, sometimes called “Gabriel’s Horn.” The bucket
(or horn, if you prefer) can be filled by a finite amount of paint but
requires an infinite amount of paint to coat its surface area. Skim the Wikipedia article on
the subject. Have you ever before seen a situation where the boundary between
the finite and the infinite is infinitesimally thin?
Fourth, we would orally identify the techniques of differentiation or
antidifferentiation that would be appropriate for §9-11 #1-100 all. (This
takes quite a while.)
For example, here is what I would expect from the class.
#1, 2. CR + PR
#3, 4. integration by parts
#5, 6, 9, 10, 17, 18. power rule, CR
#7, 8. u substitution (u = 3x + 5 or u = 5 – 2x, respectively)
#11, 12. formulas from p. 452
#13, 14. QR
#15, 16. long division followed by partial fraction decomposition
#19, 20. trig substitution
#21, 22. power rule, deriv. of exponential, PR (automatic failure for anyone
who says 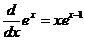 ) )
#23, 24. integration by parts
#25, 26. by formula (should be memorized from last fall)
#27, 28. integration by parts
#29, 30. choice of integration by parts (fairly easy) or trig substitution
(hard)
#31, 32. trig substitution (hard), or a table of integrals if you have one
#33, 34. by formula (memorized or easily re-derived)
#35, 36. u substitution after
applying definition of tanh x or
coth x, respectively
#37, 38. PR
#39, 40. integration by parts
#41, 42. PR
#43, 44. rapid repeated integration by parts
#45, 46. logarithmic differentiation
#47, 48. partial fraction decomposition
#49, 50. PR
[etc.]
Check through the first 50 to make sure you agree with my assessments; then
do the remaining 50 by making light notations in the margin of your textbook.
Finally, we would briefly examine pp. 495-496, some tricky substitutions for
evaluating complicated antiderivatives. These are labeled as “historical
topics” by your textbook because, in an era of computer algebra systems,
there is not much reason for HappyCal students to spend time on these.
|
|
|
M 2/25/08
|
HW due:
First, be sure you have read through Friday’s lesson plan (see calendar entry
for Friday) and have executed all the steps. (This does not count toward your
35 minutes, since it should have been done on Friday when you were stuck at
home looking at the icy tree branches.) For example, there might be a brief
quiz to spot-check to see whether you had visited the Wikipedia entry for
Gabriel’s horn.
Then, write §9-10 #23, §9-11 #1-100.
Regarding the §9-11 problem group, do as many as you can tolerate. Omit ones
that are too easy (e.g., #14) or too hard (e.g., #31) to have much
educational value, and avoid busywork. Only you know which ones you need to
focus on. At a minimum, please include #19, 20, 52 (without reduction
formula), 67 (without calculator), 68 (without calculator), 73, 74, and 77-80
all. You may use reduction formulas for problems such as #54 and 56 that cry
out for them, and you may use your calculator to check #67 and 68.
Some reduction formulas will be provided on Wednesday’s test. However, you
should be able to handle simple problems (e.g., #53) by using integration by
parts and/or trigonometric identities such as those on p. 452.
|
|
|
T 2/26/08
|
HW due:
Continue reviewing for your test. The skill of quickly identifying the type of problem (as in §9-11 #1-100)
is crucial. Finish up as many of these as you can, being sure to include the ones
listed below at a minimum, and spend any additional time available working on
R or T problems at the end of the chapter. Do all of the identifications.
§9-11 #19, 20, 52 (without reduction formula), 67 (without calc.), 68
(without calc.), 73, 74, 77-80 all.
In class: review.
|
|
|
W 2/27/08
|
Test (100 pts.) on Chapter 9.
|
|
|
Th 2/28/08
|
HW due:
Read §§10-1, 10-2. This is mostly a review of previously discussed material.
|
|
|
F 2/29/08
|
HW due: Read
§10-3; write §10-2 #11, 12, 13, §10-3 #1ab, 2ab, 3a, 4a, 5a, 6a, 7-11 odd.
|
|