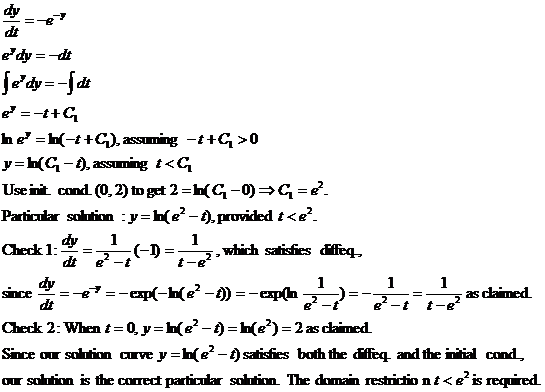|
M 12/3/07
|
HW due: Write §7-3 #3, 4. Use the example problems and the
answers for #3 (checked only when you are stuck) to help you in working #4.
|
|
|
T 12/4/07
|
HW due: Read §7-4; patch up existing deficiencies and write
§7-3 #9.
|
|
|
W 12/5/07
|
HW due: Write §7-4 #2, 3, 4. Photocopying and graph paper
are not required. However, graph paper is recommended.
The solution to §7-3 #9 will be posted at a future time, and when it is, you
will be held accountable for it. (It is not as hard as it looks, but there
are a large number of places where you can take a wrong turn.) I will let you
know when this occurs so that it does not take you by surprise. In the meantime,
we will work on some simpler diffeqs.
|
|
|
Th 12/6/07
|
HW due: Read §7-5; write §7-4 #7, 8.
Also, if time permits, please send some anonymous e-mail feedback by clicking
here.
Important: When asked, please type
Stu Dent as your name and happycal [at sign] modd.net as your address so that
I cannot tell who you are. If you enter a truly phony e-mail address such as
happycal [at sign] stuvwxy.com, the message will not be delivered—it will
simply go into the bit bucket and nobody will ever see it again. You must use
a plausible address for a real website, such as modd.net, so that the message
will be delivered to me.
What do you enjoy about our class? What do you dislike? Are audio-visual aids
(SmartBoard, chalkboard, videos, etc.) being used effectively? Are you
learning? Are you bored? What you would you like to tell Mr. Hansen to do
differently—or do more of? These are the kinds of things I want to know
about.
|
|
|
F 12/7/07
|
HW due: Write §7-5 #1, 2. For #1, please enter the heading
for dy as dy = slope · 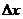 as a way of
reinforcing how you calculate dy. (In plain English: “The change in the
linear approximator equals the slope times the step size.”) For #2, please
enter the program shown below. as a way of
reinforcing how you calculate dy. (In plain English: “The change in the
linear approximator equals the slope times the step size.”) For #2, please
enter the program shown below.
PRGM NEW
EULER
(Press ENTER key to get the “:” prompt.)
:ClrHome
:Disp "PROGRAM: EULER"
:Output(3,1,"WRITTEN BY E.M. ")
:Output(4,1,"HANSEN, ST. ")
:Output(5,1,"ALBANS SCHOOL. ")
:Output(6,1,"Y1 IS ASSUMED TO")
:Output(7,1,"CONTAIN DY/DX. ")
:Output(8,1,"")
:0 I I
:ClrList L1,L2
:Prompt X,Y,N,H
:Lbl A
:I+1 I I
:Y+HY1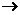 Y Y
:X+H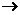 X X
:X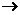 L1(I) L1(I)
:Y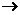 L2(I) L2(I)
:If I<N
:Then
:Goto A
:End
:Disp "CHECK L1,L2"
2nd QUIT
To execute program, enter your diffeq. into Y1 (using ALPHA Y for Y), use 2nd
QUIT to return to the calculator mode, issue the command PRGM EXEC EULER, and
press ENTER.
To display the estimated points on the solution track, use 2nd STAT PLOT,
turn Plot1 on, and use the first pictograph (representing a scatterplot) to
define Xlist as L1 and Ylist as L2. Then press ZOOM 9
to view.
|
|
|
M 12/10/07
|
No additional written work due. Use this time to get
caught up on older assignments, or work ahead on tomorrow’s assignment.
|
|
|
T 12/11/07
|
HW due: Read §7-6; write §7-5 #7, 8; write §7-6 #13, 14,
15. You are encouraged to use your EULER program to help you.
|
|
|
W 12/12/07
|
HW due: Prepare a list of review problems that you intend
to work on, and work on at least 35 minutes’ worth. Unassigned HW problems,
“Q” problems, and the problems at the ends of the chapters are all good
sources of material.
In class: Review.
|
|
|
Th 12/13/07
|
Test (100
pts.) on §6-8, §6-9, and all of Chapter 7.
Here is the problem we did near the end of class yesterday:
Make a slope field on 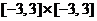 and solve the
diffeq. dy/dt = –e–y subject to initial condition
(0, 2). Then use Euler’s method manually with a and solve the
diffeq. dy/dt = –e–y subject to initial condition
(0, 2). Then use Euler’s method manually with a 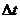 value of 0.5 to
estimate y at time t = –1. value of 0.5 to
estimate y at time t = –1.
Because it appeared that everyone was getting the slope field plotted
correctly, I will not post it here. (You can use BIGSLOPE to check your
sketch now, though perhaps not during the test.)
To solve the diffeq., we separate variables and antidifferentiate both sides:
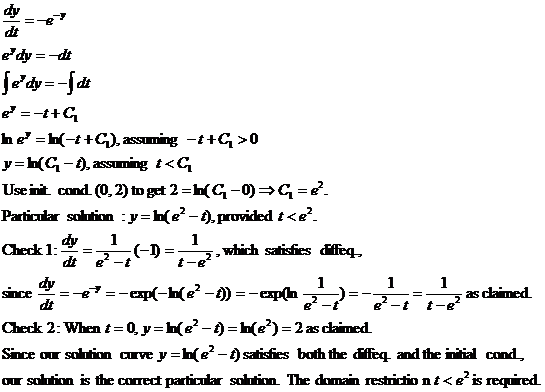
|
|
|
|
Euler’s
Method. Since the step size was
given as –0.5, and since time t =
–1 is the goal of Euler’s estimation, we know that we will be making two Euler
steps. The table below is a good way to show the work. Remember, we never
round until the end of the problem, but we use “. . .” when recording decimal
values in order to avoid wasting time.
|
|
|
|
i
|
ti
|
yi
|
slope
|
dy= slope · 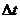
|
yi + 1 = new
estimated y value
|
|
|
|
0
|
0
|
2
|
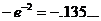
|
(–.135...)(–.5) = 0.067...
|
2 + .067...=2.067...
|
|
|
|
1
|
–0.5
|
2.067...
|
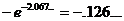
|
(–.126...)(–.5) = 0.0632...
|
2.067... + 0.0632... = 2.1309...
|
|
|
|
2
|
–1.0
|
2.1309...
|
STOP.
|
|
|
|
|
|
We must stop after making two full Euler steps, since our estimated data
point is now (–1.0, 2.1309). It is a common student error to go on for another
step or two, but on the AP exam, you will earn credit only if you answer the
question that was posed, namely the value of y that is predicted when t
= –1.
When t = –1, the true solution
track gives y = ln(e2 – t) = ln(e2 –
(–1)) = 2.1269..., from which we see that the Euler’s Method estimate is
quite accurate. Why is the Euler estimate too high? The explanation is the
downward concavity of the solution. Downward concavity is readily seen in the
slope field near (0, 2), but one can also prove downward concavity by
computing the second derivative, as follows:
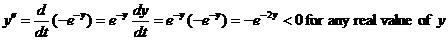
Downward concavity means that the Euler estimates, which always follow linear
tracks, will always be greater than the true solution values as we step to
the right or left of the initial point. The reason is that the solution is
always curving downward away from the Euler linear approximator.
The opposite is true for solutions that have upward concavity. Euler
estimates in those cases, whether to the left or to the right of the initial
condition, will always tend to be too low when compared to the true solution
values.
For the truly interesting slope fields that involve a mixture of both
downward and upward concavity, Euler’s Method can be whipsawed and can
sometimes be fooled into losing track of the original solution altogether,
especially if the step size is too large.
For those of you who are thinking ahead, you may be wondering (1) why do we
use Euler’s method if it introduces systematic errors of this sort, and (2)
if the errors are truly systematic, why can’t we take them into account and
thereby improve accuracy? Here are the answers:
1. Most diffeqs. of real-world interest cannot be solved exactly. The problem
I gave you is a rare exception, a separable first-order diffeq. for which it
is relatively easy to find an exact solution. Most diffeqs. you will
encounter are either much more difficult to solve in a closed form or (more
often than not) completely impossible.
2. We can often use higher-order
methods to improve accuracy. These are versions of Euler’s method that
use not only the slope information, but also true or estimated information
about the second, third, fourth, etc. derivatives as a way of bending the
estimated track (as David Beckham might) so that it follows the true solution
more closely. The tradeoff is that these methods are more complex to
implement and are much more expensive (in terms of computing power) than the
simple Euler’s Method. If speed is more important than accuracy, Euler’s
Method will often be good enough, especially if the step size can be kept
fairly small so that the errors do not accumulate too quickly.
|
|
|
F 12/14/07
|
HW due: Re-do your entire test
from yesterday. It is approximately a 35-minute test, and I do expect you to
finish it during your homework time. The questions about slope fields,
differential equations, and Euler’s Method are all exactly within the
framework of what you should have been expecting and what will be given to
you on the AP exam. The first 3 questions were, admittedly, of a more tricky
nature.
|
|
|
M 12/17/07
|
HW due: Read §§8-1 and 8-2 carefully. There is no written
work due, but be sure to take good reading notes, since an open-notes quiz on
the basics is possible.
|
|
|
T 12/18/07
|
HW due: Read §8-3; write §8-2 #13-20 all. In #13-18, pick
at least one point of interest in each problem, and justify why it is what it
is using words (this is a skill the
AP exam requires). Try to mix things up a bit so that you are sometimes
talking about local extrema, sometimes about plateau points, sometimes about
points of inflection, and so on.
Example: In #13, there is a local max. when x = –2 since 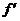 changes sign there
from positive to negative. (Or, you could say that there is a local max. when
x = –2 since changes sign there
from positive to negative. (Or, you could say that there is a local max. when
x = –2 since 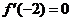 , indicating a horizontal tangent, and , indicating a horizontal tangent, and 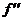 is negative.) is negative.)
|
|
|
W 12/19/07
|
HW due: Read §8-4 (the last new material we will do before
the midterm break); write §8-3 #2, 4. Please note that when you justify your
answers, you should follow the AP standard. Calculator justifications are not
permitted; you must give calculus reasons (e.g., “x = 1/8 provides a local min. for the f (x) area function
since 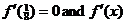 changes sign from
negative to positive at x = 1/8, as
shown by the algebraic work below”). changes sign from
negative to positive at x = 1/8, as
shown by the algebraic work below”).
To demonstrate a sign change in the first or second derivative, you cannot
simply check values to the left and to the right. You must demonstrate
through algebra that x values less
than the value of interest produce an expression having one sign, and x values greater than the value of
interest produce another sign.
An example may help clarify this last point. If 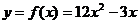 , then it is easily proved that the first derivative
changes sign at x = 1/8, since , then it is easily proved that the first derivative
changes sign at x = 1/8, since 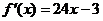 is equal to 0 when x = 1/8, and we can easily solve the inequalities is equal to 0 when x = 1/8, and we can easily solve the inequalities
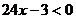 and and 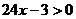 to find the
conditions on x that produce
negative and positive values for the first derivative, respectively. In this
example, the first derivative has a sign change from negative to positive at x = 1/8, meaning that x = 1/8 is associated with a local
min. for function f. to find the
conditions on x that produce
negative and positive values for the first derivative, respectively. In this
example, the first derivative has a sign change from negative to positive at x = 1/8, meaning that x = 1/8 is associated with a local
min. for function f.
|
|
|
Th 12/20/07
|
No additional written HW due. If you have time,
please revise your §8-3 problems to conform to the format we discussed. There
may be another quiz.
|
|
|
F 12/21/07
|
No additional written HW due (in part, to allow you
to attend the Lessons and Carols service). A quiz on optimization terminology
and basic minimization and maximization techniques is likely.
|
|