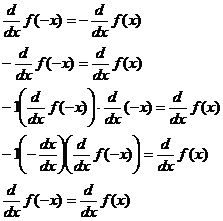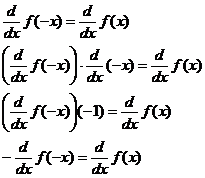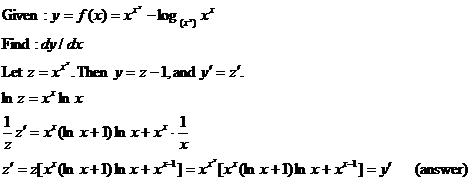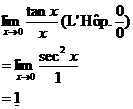Monthly Schedule

(Honors AP Calculus, Period C)

Th 11/1/07	HW due: Read Braxton’s direct proof of FTC2 and Mr. Hansen’s proof that FTC1 implies FTC2 and conversely. No additional written work is due. Work on your college essays and/or trick-or-treating.
F 11/2/07	No school (teacher work day).
M 11/5/07	HW due: Read §5-10; write §5-9 #5-25 odd, 31-37 all.
T 11/6/07	IMPORTANT: Class will meet today in Steuart 302. HW due: Write §5-10 #4, 7.
W 11/7/07	HW due: Read §5-11; write §5-11 #1, 6; p. 241 #1; also answer the problem below. Prove that (2M + T)/3 gives Simpson’s Rule, where M denotes the result of a midpoint rule Riemann sum and T denotes the result of a trapezoid rule approximation. Hint: For M and T, use half as many intervals as for Simpson’s Rule. In other words, let the mesh points be x0, x1, x2, x3, . . . , where the even-numbered ones are involved in T and the odd-numbered ones are involved in M.
Th 11/8/07	HW due: Read §§6-1 through 6-3; write §6-1 #1-7 all, plus write from memory the proof that is irrational. (You may consult your notes, but only if necessary.)
F 11/9/07	HW due: §6-3 #3-54 mo3 plus 46, 47, and the following problem: Prove that is even if f is odd, and odd if f is even. Quiz on FTC1 (statement), FTC2 (statement found on p. 255), the equivalence of the two (discussed previously in class), and applications of the fact that ln x is an antiderivative of the reciprocal function. After quiz: Fun Friday activity.
M 11/12/07	FLASH UPDATE! The assignment listed below has been postponed until Tuesday in celebration of the Bulldogs’ 11-7 victory over the Landon Bears in Saturday’s IAC championship football game. If you wish to work ahead a day, you may—or you can enjoy a pleasant weekend of relaxation and celebration. HW due: Read §6-4 (review of precalculus) and §6-5; write §6-4 #Q1-Q10, 8, 12, 13; write §6-5 #1, 5. Then, carefully explain the errors in the following proofs that is even if f is odd, and is odd if f is even. You may find the 3 final questions at the bottom helpful as you search for the errors. The errors may seem minor at first but are of great importance in your study of the calculus. First proof. WARNING: This is a false proof containing errors. See if you can find them. Given: f is an odd function, i.e., Prove: df/dx is an even function. Take derivatives of both sides of the equation and proceed from there: Therefore, the derivative is an even function (since for any x, the behavior by the derivative is the same as the behavior would be for –x). (Q.E.D.) Second proof. WARNING: This is a false proof containing errors. See if you can find them. Given: f is an even function, i.e., Prove: df/dx is an odd function. Take derivatives of both sides of the equation and proceed from there: Therefore, the derivative is an odd function (since for any x, the behavior by the derivative is the additive inverse of the result that would be obtained by using –x instead). (Q.E.D.) Final questions: (1) In general, is it true that If not, why not, and what would you change to make a true equation? (2) Suppose the argument of function f is replaced by some function of x. This could be a simple function, maybe even something really simple like the additive inverse function. Is it true, in general, that If not, why not, and what would you change to make a true equation? (3) Suppose that the argument of function f is made completely general, i.e., replaced by function g(x). Is it true, in general, that If not, why not, and what would you change to make a true equation?
T 11/13/07	HW due: No additional HW due, but make sure you have finished the assignment listed in yesterday’s calendar entry.
W 11/14/07	HW due: Read §6-6; write §6-5 #20-32 even.
Th 11/15/07	HW due: Read §6-7; write §6-6 #5-12 all, 21, and the following: Prove that if f (x) = logb x, then . Show all steps, and provide a reason for each one. Most of these steps can simply be copied from pp. 273-274, but try to do the proof without referring to the book unless necessary.
F 11/16/07	HW due: Write §6-7 #3-54 mo3. In class: Review. By the way, thanks to those who spotted the error I made in yesterday’s challenge problem. (The irony, of course, is that the problem uses the derivative of x^x as a lemma, and only a few minutes earlier, I had correctly given you that derivative.) Here is the correct solution:
M 11/19/07	Test (100 pts.) on all recent material. Suggested review problems are all the “R” problems at the end of Chapter 6 except for the limit problems requiring L’Hôpital’s Rule. Format of the test will be predominantly multiple-choice. Proofs you are responsible for are FTC1 FTC2, FTC2 FTC1, the change-of-base formula, and the Rule of 69/72. Also, explain why the following riddle has the answer of “houseboat”: Answer (don’t peek until you’re ready to check!):
T 11/20/07	HW due: Read §6-8 on L’Hôpital’s Rule. Reading notes are required, as always. In class: After a short discussion on L’Hôpital’s Rule, we will welcome our guest speaker, Mr. Joe Morris, STA ’62.
M 11/26/07	HW due: Read §6-9; write §6-8 #3-30 mo3, plus 22, 23, 31, 32. Be sure to write “lim” repeatedly when showing your work, and be sure to show the “L’Hôp.” justification at the appropriate point(s). The first one is done for you as an example below. 3.
T 11/27/07	HW due: Finish all L’Hôpital’s Rule problems previously assigned; then work for 35 minutes on §6-9 # 1-90. (Do as many as you can. These are all good problems, and we will go through most of them orally in class.)
W 11/28/07	HW due: Finish as many of the remaining problems in §6-9 as possible. Make sure to include a good selection from several categories.
Th 11/29/07	HW due: Read §7-1 and §7-2; write §7-2 #2, 5, 6, 9.
F 11/30/07	HW due: Read §7-3; write §7-2 #8, and put the finishing touches on any of the previously assigned problems.

---

Return to the HappyCal Zone

Return to Mr. Hansen’s home page

Return to Mathematics Department home page

Return to St. Albans home page

Last updated: 03 Dec 2007