|
|
Given:
(1) f is cont. on domain [a,
b]
(2) m = min. value of f on [a, b]; in other words, 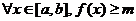
(3) M = max. value
of f on [a, b]; in other words, 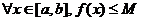
Prove: Rf = [m, M]
Proof:
First, note that m and M exist and are well-defined real
numbers by EVT. We will use a set-theoretic argument to show that Rf =
[m, M].
If y1 < m, then there exists no value 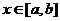 such that f (x)
= y1. The reason is that
if we assumed (bwoc) that such an x existed, then f (x) = y1 < m, contradicting the given statement (2). such that f (x)
= y1. The reason is that
if we assumed (bwoc) that such an x existed, then f (x) = y1 < m, contradicting the given statement (2).
Similarly, if y2 > M, then there exists no value 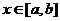 such that f (x)
= y2. The reason is that
if we assumed (bwoc) that such an x existed, then f (x) = y2 > M, contradicting statement (3). such that f (x)
= y2. The reason is that
if we assumed (bwoc) that such an x existed, then f (x) = y2 > M, contradicting statement (3).
Since y1 and y2were both chosen wlog, any y value less than m or greater than M
cannot be in Rf.
Therefore,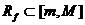 . (*) . (*)
For y3 = m, EVT states that 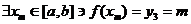 . (**) . (**)
Similary, for y4
= M, EVT states that
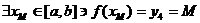 . (***) . (***)
If m = M, then f is constant
on [a, b] and the conclusion Rf = [m,
M] = {m} would be true, since it is merely asserting that
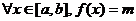 . .
Having m > M is impossible (a minimum cannot exceed a maximum). That
statement is considered obvious, but a rigorous proof can be made as follows.
Assume (bwoc) that 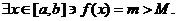 However, by
definition of “maximum,” M is a y value such that However, by
definition of “maximum,” M is a y value such that 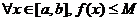 , a contradiction. , a contradiction.
In the previous paragraphs, we established that m = M satisfies the
theorem trivially, and m > M is impossible. Therefore, let us
assume wlog that m < M. In that case,
xm
cannot equal xM
since f was given to be a function
and thus cannot produce differing y
values (namely, m and M) for the same x value. Therefore, we can consider either the interval I = [xm, xM]
if xm
< xM
or the interval I = [xM, xm]
if xm
> xM.
Either way, we can now apply IVT to function f on closed interval I
to conclude that 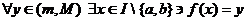 . However, this statement is needlessly complicated. We
refer to interval I \ {a, b},
that is, I without its endpoints, in
the IVT conclusion since that is what IVT says. However, IVT remains true if
we weaken its conclusion by considering larger intervals. By definition
(above) of xm
and xM,
we know that both xm
and xM
are in [a, b]. Therefore, . However, this statement is needlessly complicated. We
refer to interval I \ {a, b},
that is, I without its endpoints, in
the IVT conclusion since that is what IVT says. However, IVT remains true if
we weaken its conclusion by considering larger intervals. By definition
(above) of xm
and xM,
we know that both xm
and xM
are in [a, b]. Therefore, 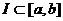 , and our conclusion based on IVT becomes the following: , and our conclusion based on IVT becomes the following:
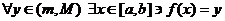
When we combine this with (**) and (***) above and note that 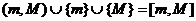 , we can rewrite the conlusion as
follows: , we can rewrite the conlusion as
follows:
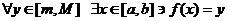 . .
This last condition establishes that 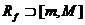 , or in English, that the range of f is at least big enough to include all of the values from m to M inclusive. , or in English, that the range of f is at least big enough to include all of the values from m to M inclusive.
Since we already proved in (*) that Rf is a subset of [m, M], the conclusion
is that Rf
= [m, M].
(Q.E.D.)
Comment: Showing that two sets are
equal since one of them both contains and is contained in the other is akin
to showing that two propositions are equivalent since each one implies the
other.
|