|
|
Problem:
Prove that at any time t, there
must be at least one pair of antipodal points along the equator having identical
temperature.
Hints: You may assume that there
are no discontinuities in temperature and that sums and differences of
continuous functions are continuous. Treat the earth as a sphere, even though
in reality it is slightly pear-shaped. The word “antipodal” refers to a pair
of points that are on opposite sides of the earth, i.e., two points that
could be connected by a diameter.
|
|
|
Solution:
Assume wlog that time t = t0 has
been specified, and let P be the
point at the intersection of the equator and the Greenwich Meridian (0
degrees longitude). Define T(x) to be equatorial temperature at
time t0 as a function of
position, where x denotes degrees
of longitude east of Greenwich.
Using this notation, the domain for T
is [0, 360], and the temperature at time t0
at point P can be written either as
T(0) or as
T(360).
The antipodal temperature for any position x is given (sloppily) by T(x 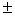 180). This notation,
while imprecise, recognizes that one must either add or subtract 180,
depending on the value of x, in
order to find the position of the antipode. The 180). This notation,
while imprecise, recognizes that one must either add or subtract 180,
depending on the value of x, in
order to find the position of the antipode. The 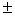 symbol is normally
read as “plus or minus,” which makes this notation technically invalid, since
usually only one of the two values will lie in the domain of T. Therefore, a better notation for
the antipodal temperature for position x
is T((x + 180) mod 360). symbol is normally
read as “plus or minus,” which makes this notation technically invalid, since
usually only one of the two values will lie in the domain of T. Therefore, a better notation for
the antipodal temperature for position x
is T((x + 180) mod 360).
Now define D(x) to be the difference in temperature between a point at
position x and a point at the
antipode of x. For example, D(0) means the difference in
temperature between P and the
antipode of P, where the antipode’s
coordinates are latitude 0° N, longitude 180° E.
In other words,
[Equation
1] D(0) = T(0) – T(180)
To put this in more general terms,
[Equation
2] D(x)
= T(x) – T((x + 180) mod 360)
where x is any value on the closed
interval [0, 360]. For x 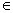 [0, 180], Equation 2
can be simplified considerably, as follows: [0, 180], Equation 2
can be simplified considerably, as follows:
[Equation
3] D(x)
= T(x) – T(x + 180)
If D(0) = 0, the proof would be
complete because P (at position 0)
and its antipode (at position 180) would constitute the pair that the problem
asked us to find. Therefore, assume wlog that D(0) 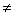 0. 0.
Observe that by Equation 3, we have
[Equation
4] D(180) = T(180) − T(360)
Since T(360) is another name for T(0), the temperature at point P, we can substitute to get
[Equation
5] D(180) = T(180) − T(0)
Comparing Equation 1 and Equation 5, we see that D(0) and D(180) are two
nonzero values having opposite signs. Since T can be assumed to be a continuous function, D is also a continuous function.
Therefore, apply IVT to function D
on the closed interval [0, 180]. The intermediate value we wish to attain is
0, which is strictly between D(0) and its additive inverse D(180).
By IVT, there must be at least one value x0
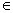 (0, 180) such that D(x0)
attains the intermediate value of 0. But if D(x0) = 0,
then by the definition of function D,
T(x0) minus the temperature at the antipode of x0 must equal 0. In plain
English, x0 and its
antipode have the same temperature. (Q.E.D.) (0, 180) such that D(x0)
attains the intermediate value of 0. But if D(x0) = 0,
then by the definition of function D,
T(x0) minus the temperature at the antipode of x0 must equal 0. In plain
English, x0 and its
antipode have the same temperature. (Q.E.D.)
|