Geometry / Mr. Hansen 4/10/2008

Name: _________________________

Test on Chapter 12 Plus §§13.1-13.3: 100 pts., No Calculator

• Mathematics is about communication more than it is about calculating answers. Therefore, problems requiring work or explanation are usually scored with a minority of the points for the answer and most of the points for your work or explanation.
• Illegible or cryptic explanations may not earn full credit, even if your answers are correct.
• Read all instructions. Be clear and concise in answers. Ditto marks are acceptable.
• If you obtain an answer that you know is wrong, mark it with “NR” for Not Reasonable. More partial credit is available if you indicate that you know something is amiss. A small deduction will be made if you mark “NR” on a correct solution, however.
• If an answer involves messy arithmetic, you may leave it unsimplified unless the problem says that simplification is required. For example, if the answer to a problem is 15 times 3/7, with the entire quantity raised to the 4th power, you may simply write (15 · 3/7)⁴.
• Simple radical form means no radicals in the denominator, no embedded perfect square factors under the radical sign, and no fractions or rational decimals under the radical sign. On today’s test, simple radical form is not required unless specifically requested.

Part I: Always, Sometimes, Never with Explanations (6 pts. each)

In the small blank (2 pts.), write A if the statement is always true, S if sometimes true, or N if never true. Then give explanations, diagrams, counterexamples, etc. (4 pts.) to justify your answer. The explanation may be quite brief (if you cite a theorem, for example).

___1.	The volume of a pyramid equals half the volume of a prism having the same height and base area.
	________________________________
	________________________________
	________________________________
___2.	A circle has the same area as a square.
	________________________________
	________________________________
	________________________________
___3.	If two similar pyramids have heights of 3 inches and 6 inches, respectively, then the volume of the larger pyramid is 4 times the volume of the smaller pyramid.
	________________________________
	________________________________
	________________________________
___4.	The slope of the linear equation ax + by + c = 0 equals a/b.
	________________________________
	________________________________
	________________________________

___5.	Two spherical planets whose radii are in a 100:1 ratio have volumes that are approximately in the ratio of 100,000:1.
	________________________________
	________________________________
	________________________________
___6.	Volume is measured in square units.
	________________________________
	________________________________
	________________________________
___7.	The surface area of a hemisphere (domed part only) equals half the area of the circular base.
	________________________________
	________________________________
	________________________________

Part II: Basic Skills (20 pts.)

Give each answer as a fraction or improper fraction in lowest terms. See example on board. No credit at all will be given for mixed numbers (a.k.a. mixed fractions).

8.
9.	=
10.	If , then x must equal _______
11.

Part III: Descriptive Problems, Traditional + Reform Math (19 pts. each)

Solve each problem with correct answers (“traditional math”), as well as providing careful and adequate explanation for each step of your procedure (“reform math”). If you cannot do both, then do the best you can in order to earn partial credit.

12.


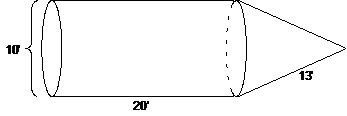
Calculate the volume and total surface area of the rocket body shown. It is formed from a right circular cylinder joined to a right circular cone. (Remember to show units. A single quote mark means “feet.”)

13. A line l, having equation 2x – 3y = 5, passes through the point P = (4, a). Find the equation of the line, in slope-intercept form, that is perpendicular to l at point P. A sketch is required in order to earn full credit.