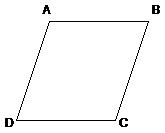Geometry / Mr. Hansen 11/16/2007

Name: ___________KEY___________

Proof (10 pts.)

Use a 2-column proof to show that in a rhombus that is not a square, there is at least one acute angle.
Given: ABCD is a rhombus ABCD is not a square
Prove: At least one of ABCD’s angles is acute
_________________________________________________________________
1. ABCD is a rhombus	|  1. Given
2. ABCD is not a square	|  2. Given
3. None of ABCD’s angles are acute	|  3. Assume bwoc [negation of concl.]
4.	|  4. Def. acute [or, def. “nonacute”]
5. supp.	|  5. Prop. of parallelogram: consec. supp.
6.	|  6. Def supp.
7.	|  7. Reasoning from 4 and 6 [only way to keep sum from exceeding 180 is if both measures are exactly 90]
8. and are rt.	|  8. Def. rt.
9. ABCD is a rectangle	|  9. Parallelogram with at least one rt.
10. ABCD is a square	|  10. Rhombus and rect. square (1, 9)
	|  Steps 2, 10
(Q.E.D.)
Alternate version (streamlined)
_________________________________________________________________
1. ABCD is a rhombus	|  1. Given
2. ABCD is not a square	|  2. Given
3. ABCD’s angles are all nonacute	|  3. Assume bwoc [negation of concl.]
4. supp.	|  4. Prop. of parallelogram: consec. supp.
5. Supp. A and B must be right or a pair in which one is obtuse and the other is acute	|  5. Prop. of supp. [discussed in class]
	Either way, there is a contradiction. If angles A and B are rt. , ABCD is a rectangle, hence a square, contradicting step 2. If the pair is acute-obtuse or obtuse-acute, then step 3 is contradicted.
(Q.E.D.)