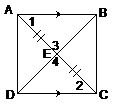Geometry / Mr. Hansen 11/17/2007

Name: ___________KEY___________

Homework Answers (§5.7)

2.	Assume (bwoc) that ABCD is a rhombus. Then AD = AB, which forces x = 11. But then BC = 3x – 2 = 3(11) – 2 = 33 – 2 = 31. This is a contradiction, since each side was supposed to be 27.
3.	Since must be 90°, 2x + 6 must be 48. Answer: x = 21.
6a.	Diagonals that are bis. of each other rhombus (def. prop. of a rhombus).
b.	The only way Kenny can look like Renny is to be Mr. Square. Answer: square.
c.	Consec. supp. parallelogram opp. congruent. But we were also given opp. supp. By CASA, opp. are right . Answer: rectangle.
d.	If the parallel sides are congruent, we have a parallelogram by #3 on p. 249. However, if the parallel sides are not congruent, we have the same problem as #13c on p. 260, namely an isosceles trapezoid. There are two incompatible cases that are possible: Pete Peterson or Izzy the isosceles trapezoid. Answer: quadrilateral.
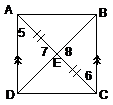
8.	_________________________________________________________________
	1. YTWX is a parallelogram	|  1. Given
	2.	|  2. Given
	3.	|  3. Given
	4.	|  4. Given
	5. are rt.	|  5. Def.
	6.	|  6. All rt. are
	7.	|  7. Refl.
	8.	|  8. ASA (7, 4, 6)
	9.	|  9. CPCTC
	10.	|  10. Prop. of parallelogram: opp. sides
	11.	|  11. Trans. (9, 10)
	12. TWXY is a rhombus	|  12. Def. prop. of rhombus: all 4 sides
	(Q.E.D.)
13a.	A pair of opp. sides both || and parallelogram (a defining property).
b.	The sides of length 8 and 10 are || (since both are to a third coplanar line), meaning that we have at least a trapezoid. Is this an isosceles trapezoid? No, since an isosceles trapezoid must have two acute angles and two obtuse angles. Is this a kite or a parallelogram? No, since the Zoid clan is completely separate from Kenny and the Petersons. Answer: trapezoid.
c.	The sides of length 6 and 10 are || (given), meaning that we have at least a trapezoid. Since the other sides are (given), this is an isosceles trapezoid.
d.	Opp. (given) parallelogram. Therefore, consecutive are supp. However, consecutive are also congruent (given). By CASA, all angles are right. Answer: rectangle.
e.	Diagonals bis. each other parallelogram. Since diagonals are also , and since the only parallelograms having diagonals are rectangles, this must be a rectangle.
f.	Diagonals bis. each other rhombus (a defining property).
g.	One diagonal bis. the other kite (a defining property).
h.	One diagonal bis. the other nothing special. This could be a kite, a rhombus, a rectangle, a square, or an ugly boring quadrilateral with no name. (Try sketching one of each type.) Answer: quadrilateral.
	Strange fact: In #13h, the figure could not be a trapezoid. Do you see why not? If one diagonal bisects the other, and if there is a pair of parallel sides, then it is possible to prove that the other diagonal is bisected as well. However, if the diagonals bisect each other, we have a parallelogram . Here is the given figure, marked up in two different ways to show why a trapezoid is impossible. Case I: Parallel lines at top and bottom of diagram. If ABCD is a trapezoid with , then by alt. int., (given), and by vert. angles. Therefore, by ASA, from which we get by CPCTC. Since the diagonals bisect each other, ABCD is a parallelogram . According to our book’s definition, a trapezoid is a quadrilateral with exactly one pair of opposite sides parallel, while a parallelogram must have both pairs of opposite sides parallel. Case II: Parallel lines at left and right of diagram. The proof is similar to Case I and is left as an exercise for you.
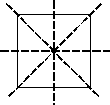
17a.	Imagine making a paper model of the quadrilateral. “Symmetrical across both diagonals” means that the model can be folded along either diagonal so that the edges line up. If you fold along both diagonals and then unfold, you would see creases that divide the figure into 4 congruent triangles. We learned that the 4 congruent triangles (“quadruplets”) are a defining property of Rhonda the Rhombus. Answer: rhombus.
b.	“Symmetrical across exactly one diagonal” means that the figure can be folded so that two congruent triangles (by SSS) are formed. We learned that this happens with a kite. However, since the problem said “exactly one,” we must rule out kites that are rhombuses, for otherwise we would have symmetry across two diagonals. Answer: a kite that is not a rhombus.
c.	Only Mr. Square has four dotted lines that create matchups. Answer: square.