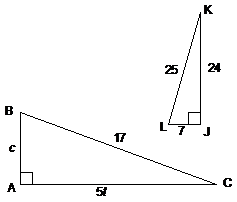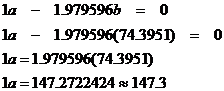|
Th
5/1/08
|
HW due: Read and underline the sentence in the
middle of p. 667 that begins with the phrase, “Notice that in constructions .
. .” Then read sample problems 2 and 3 on p.670, read Construction 8 on p.
674, and write §14.4 #16a, §14.5 #10, 21, 22. For #10, use a large plastic
disc, e.g., the top of an oatmeal container or a coffee can lid.
|
|
|
F
5/2/08
|
Both
classes will meet in the Mathplex today (Mathplex North computer lab). Our in-class project will be to construct the 9-point circle.
HW due: Write §14.5 #7 or 11 (your choice); then everyone must do the
following project. Make a large obtuse scalene triangle (but not too obtuse!)
using a straightedge. Using compass and straightedge, construct the orthocenter, circumcenter, and centroid.
Demonstrate by example that these three points appear to be collinear. If
they are not, then you know you made a mistake and need to start over.
|
|
|
M
5/5/08
|
HW due: Write §14.6 #18, including a paragraph that
describes your procedure (step by step) and a second paragraph that explains
why your method is valid.
Here is the hypotenuse segment whose length you should copy (using your
compass to measure the length): _________________________
Here is the altitude segment whose length you should copy (using your compass
to measure the length): __________
Note 1: These are not blanks to
fill in! These are segments whose lengths you should use in your diagram.
Note 2: Hints are available by
e-mail if you provide a description of some things you have tried. “I don’t
know where to start” does not qualify as a description. You do know where to
start. You have been given two lengths, and these can be copied to a pair of
working lines in your diagram and placed perpendicular to each other by means
of a construction procedure we have learned. If you have forgotten how to construct
a perpendicular line, you can find the procedure on the Internet or in your
textbook.
Below are your scores for the 9-point circle project (worth 9 points,
logically enough). If you have not finished, you may make up the work during
Math Lab this afternoon. If you were absent, the project will take about half
an hour; other students may be able to finish up in 5 to 10 minutes.
A period: Ben 9, Andrew 7 (will be
9 after a short visit), Fritz 9, Phineas 9, Nick 9, Christian 9, D.J. 9, all
other students 0.
F period: Nick B. 0, Griffin 0,
Colin 10, Ed 10, Jamie 10, Robert 10, all other students 9.
Up to 10 points are possible if you write a correct theorem describing the
9-point circle. However, this must be written by the person who did not write
the answer to question 1.
|
|
|
T
5/6/08
|
HW due: One more try on §14.6 #18, including a paragraph
that describes your procedure (step by step) and a second paragraph that
explains why your method is valid.
Now that you know how to use loci to approach this problem, you should be
able to solve it. This will be scored at more than the usual number of
homework points. Neatness and accuracy of presentation count.
|
|
|
W
5/7/08
|
HW due: Write §15.1 #1, 2, 6; §15.2 #1, 2, 14; p. 684 #14,
16, 19, 22, 23, 24. If you cannot finish all the problems on p. 684, do as
many as you can. All are fair game for the test. People who do a really good
job on this assignment (as judged by direct examination) can qualify for up
to 4 additional bonus pts. to apply to yesterday’s assignment.
In class: Review.
|
|
|
Th
5/8/08
|
Test (100
pts.) on Chapter 14 (all) plus §§15.1 and 15.2. Note:
Five (5) points on this test will be awarded for bringing your compass and straightedge.
If you forget, you will have to borrow mine, and that means that you may have
to wait your turn in addition to losing the 5 points.
Immunity Challenge (4 pts. max.): Write p. 683 #5, 8, 11, 12. If the
constructions (#8 and #11) are not done neatly and accurately, which I can
determine at a glance, your paper will not be accepted for grading.
There will be two constructions on the test. One will be to construct the
orthocenter of an obtuse triangle, and the other will not be announced in
advance. You might as well do #8d above with an obtuse triangle in order to
practice!
|
|
|
F
5/9/08
|
HW due: Read §15.3; write §15.3 #1-7 all.
|
|
|
M
5/12/08
|
HW due:
Read §9.9 and the Rule of SOHCAHTOA; write §9.9
#1, 2, 3.
Quiz (10 pts.) on the Rule of
SOHCAHTOA. Example problems are given below.
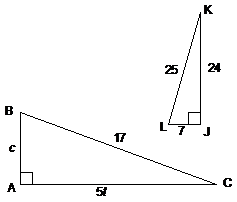
Compute each of the following:
1. sin 
2. cos 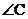
3. sin 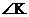
4. tan 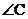
5. tan 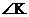
6. cos 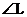
Answers:
1. 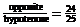
2. 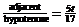
3. 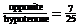
4. 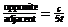
5. 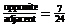
6. 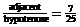
|
|
|
T
5/13/08
|
No additional HW due. I was ill and had to leave
school early, which means everyone has an evening off. If you are looking for
something productive to do, please read §9.10, the last section we will cover
this academic year.
|
|
|
W
5/14/08
|
HW due
(Mr. Barnes’ classes only): See 5/12 entry above. This is a minimal set of
problems. You should also read §9.10 and try to solve a few triangles.
HW due (Mr. Hansen’s classes): Read
§9.10; write §9.10 #4-8 all, 10. Also read through my solution of #17 (below)
and see if you can find the error(s). To earn 5 out of 4 on the HW, you need
to find all the errors.
17.(a) By symmetry, FT = 10. Then, by Pythag. Thm., PT = 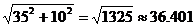 . .
(b) Since 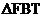 is a 45°-45°-90°
triangle, FB = is a 45°-45°-90°
triangle, FB = 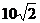 . Then, by Pythag. Thm., BP = . Then, by Pythag. Thm., BP =
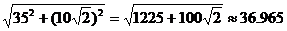 . .
(c) 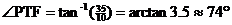 . .
(d) 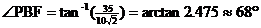
|
|
|
Th 5/15/08
|
Field Day. Depending on the weather, we will either use
trigonometry for some useful purpose (such as measuring the height of the
West Tower of the National Cathedral) or use ratios and proportions to build
a scale model of the solar system.
|
|
|
F 5/16/08
|
HW project
due (20 points):
Let z = your weight, in pounds, let
f = no. of letters in your first
name, and let l = no. of letters in
your last name.
1. Write equations expressing the values of z, f, and l. (For full credit, the z must be crossed, the f must be lower case, and the l must be written in the proper loopy
style.) For example, I would write the following:
z = 165
f = 7
l = 6
Note: You may not use these values,
since none of you weigh 165 pounds and have 7+6 letters in your name. Use the
correct values that refer to your personal situation.
2. Make a sketch in which you are suspended by two cables from a horizontal
beam. The cable on the left is to be f
+ 5 feet long, attached to the beam at point L, and the cable on the right is
to be l feet long, attached to the
beam at point R. The anchor points of the cables, L and R, should be
separated by a distance of 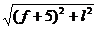 feet, which you must
compute to the nearest tenth of a foot. In your sketch, you can choose to be
attached to the cables by your waist, by your head (with something superglued
to your helmet?), or by your feet. Label the point at which you are attached
to both cables as G. feet, which you must
compute to the nearest tenth of a foot. In your sketch, you can choose to be
attached to the cables by your waist, by your head (with something superglued
to your helmet?), or by your feet. Label the point at which you are attached
to both cables as G.
3. Explain why 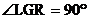 . .
4. Compute 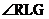 . Be sure to use the appropriate inverse trig function.
Notation must be correct for full credit. Your answer should be correct to
the nearest half degree. . Be sure to use the appropriate inverse trig function.
Notation must be correct for full credit. Your answer should be correct to
the nearest half degree.
5. Compute 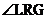 . Be sure to use the appropriate inverse trig function.
Notation must be correct for full credit. Your answer should be correct to
the nearest half degree. Then double-check your answer by computing the
complement of the angle you found in #4. (Show work for both computations.) . Be sure to use the appropriate inverse trig function.
Notation must be correct for full credit. Your answer should be correct to
the nearest half degree. Then double-check your answer by computing the
complement of the angle you found in #4. (Show work for both computations.)
6. Let a = tension (in pounds) in
the left-hand cable, and let b =
tension (in pounds) in the right-hand cable. Our goal in the next few
questions is to compute a and b. From physics, we know that when you
are at equilibrium, no longer swinging back and forth, the leftward pull,
namely 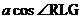 , must exactly equal the rightward pull, namely , must exactly equal the rightward pull, namely 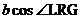 . Using the cosine values from p. 424, and estimating if
necessary (if any half degrees are involved), write the equation . Using the cosine values from p. 424, and estimating if
necessary (if any half degrees are involved), write the equation 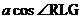 = =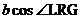 , except with the cosine values plugged in. , except with the cosine values plugged in.
7. From physics, we also know that 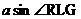 + +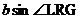 = z, since the resultant upward tension
in both cables working together must exactly counterbalance your weight, z. Write this equation, except with
the sine values and z plugged in. = z, since the resultant upward tension
in both cables working together must exactly counterbalance your weight, z. Write this equation, except with
the sine values and z plugged in.
8. Consolidate #6 and #7 into a single system of linear equations. Write down
your system.
9. Solve the system you wrote in #8. What are the values of a and b?
Note: You may see me for help on #9
if you get stuck. However, please read through the following sample solution
first.
Sample solution of a messy linear
system:
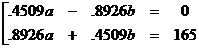
Multiply equation (1) by 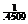 and equation (2) by and equation (2) by 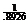 . Obviously, you will need a calculator to do this. Result: . Obviously, you will need a calculator to do this. Result:
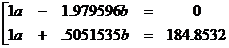
Now subtract the bottom equation from the top one, to get the following:
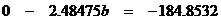
By algebra, b = 74.4 pounds,
to the nearest tenth. However, we will use a more accurate value, 74.3951, to
plug back into one of the other equations in order to find a. In this way, we reduce the
likelihood of contaminating our answer for a with inaccuracy caused by rounding b.
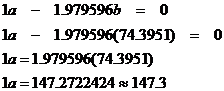
Final solution: a = 74.4
pounds, b = 147.3 pounds.
(Values are rounded to the nearest tenth.)
|
|