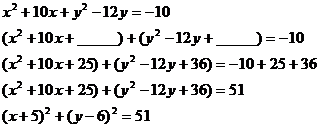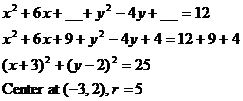|
T
4/1/08
|
HW due: Read §12.4; write §12.4 #1, 3, 4, 5, 6, 12.
|
|
|
W
4/2/08
|
HW due: Read §12.5; write §12.5 #1, 3, 5, 6, 7, 9, 10.
Note: Period A will meet in SB-002
(Steuart Building Computer Lab) starting today (Wednesday) and continuing for
the remainder of the year. Period F will continue meeting in the Mathplex.
|
|
|
Th
4/3/08
|
HW due: Read §12.6; write §12.6 #1, 3 (do both volume and total surface area), 6, 8, and the
following problem.
19. We will calculate the volume and surface area of a sphere of radius r = 3 cm, then the same computations
for a sphere of radius R = 18 cm.
Observe that the larger sphere is 6 times larger than the smaller one in
terms of the linear dimension. In other words, the ratio R : r equals 6.
(a) Vr =
________________ ; VR =
________________
(b) Compute the ratio VR
: Vr without referring
to part (a): ________________
Explain your reasoning:
_____________________________________________
(c) TSAr =
________________ ; TSAR
= ________________
(d) Compute the ratio TSAR
: TSAr without referring
to part (b): ________________
Explain your reasoning:
_____________________________________________
(e) Ignoring units, compute the ratio TSAR
: VR. You may use any of
your previously computed answers. TSAR
: VR =
_____________________________________________ . This number is meant to
symbolize the ratio of surface area to volume for a medium-sized mammal, such
as a curled-up cat.
(f) Ignoring units, compute the ratio TSAr
: Vr. You may use any of
your previously computed answers. TSAr
: Vr =
_____________________________________________ . This number is meant to
symbolize the ratio of surface area to volume for a small mammal, such as a
plump shrew or a mouse.
(g) Mammals lose heat through their skin (surface area). Explain why small
mammals must eat constantly in order to maintain their body mass (volume),
while larger mammals can survive with only a few meals a day.
________________________________________________________________________
________________________________________________________________________
|
|
|
F
4/4/08
|
HW due: Read §13.1; write §13.1 #1, 4, 8, 9, 12. This
should all be a review of Algebra I. If any of it is not completely a review for you, please make a list of your
questions. Otherwise, I will assume that you understand it (at least after
refreshing your memory from last year).
By the way, “I don’t understand” is not a question. Your questions, if you
have any, should be specific. For example, the following would be acceptable
questions:
1. What is meant by a table of values? Can I use the example on p. 605? When
I make a graph, should I make the x-axis
horizontal and the y-axis vertical?
4. Do I have to multiply the 2(x +
1) side of the equation using the distributive law? Do I need to use algebra
to transform the equation into “slope-intercept” form? Why is y = mx + b called
“slope-intercept form”?
8, 9. Does (5, 4) mean that x = 5
and y = 4? If I can plug in values
for x and y and get a true equation, does that mean that the ordered pair
satisfies the equation? Does “satisfying an equation” mean the same as “being
on the graph of an equation”?
12. If the circle is the set of points that satisfy 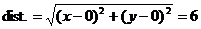 , can we square both sides to get an equation of the
circle? Is it really as simple as that? , can we square both sides to get an equation of the
circle? Is it really as simple as that?
|
|
|
M
4/7/08
|
HW due: Read §13.2; write §13.2 #4, 6, 9, 13-16. Again, as
you did for last Friday’s assignment, record questions in the margin for any
problems that seem more complicated than a review of Algebra I.
|
|
|
T
4/8/08
|
Quiz (10 pts.) on lines. Difficulty will be comparable
to §13.2 #13-17.
HW due: Read §13.3; write §13.3 #1-6 all, 9, 10.
Note: Since #9 and #10 involve
multiple parts, you will need to analyze them. I will not accept a “?” for
credit on these problems. If you cannot solve them using “traditional math,”
then you need to solve them using “reform math.” In other words, if you
cannot solve the problem, you need to describe what you would like to do in order to solve the problem. See the
example below.
12. The given line, y = 2x + 1, has slope 2 and y-intercept (0, 1). Therefore, the
question can be translated as follows:
Line 2 = line passing through (5, 3) with slope 2.
Line 3 = line passing through (5, 16) and (0, 1).
I would use point-slope to find an equation of Line 2. Then I would find the
slope of Line 3, which would allow me to use point-slope to find an equation
of Line 3.
Then I would use algebra to solve the system consisting of Line 2 and Line 3.
Note: The allure of “reform math”
is that any student capable of writing the description above would presumably
be capable of solving the problem. Therefore, the argument goes, math
teachers should focus on getting students able to describe their solution
procedure conceptually, and there is no need to worry so much about the
algebra and number-crunching. Unfortunately, it’s not quite as easy as that,
is it?
|
|
|
W
4/9/08
|
HW due:
1. Write pp. 595-596 #6-13 all. Note:
Find both volume and surface area for #11.
2. Write pp. 645-646 #9, 13, 17, 21.
3. Read the following solution of #21 on p. 597, and solve the same problem
(from scratch) with all dimensions doubled. In other words, find the volume
when the upper radius is 18, the lower radius is 24, and the partial slant
height is 12. Note: We already know
that the answer is 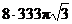 cubic units, or
approximately 14,496 cubic units, since when each linear dimension is
doubled, the volume must increase by a factor of 23, which is 8.
However, I want you to act as if you do not already know the answer to the
problem in the book. If necessary, you may copy my work below and simply
change the numbers in the appropriate places. However, you will learn more if
you read the solution and then attempt to do a complete solution to the
altered problem by subtracting the area of a small cone from the area of a
large cone. cubic units, or
approximately 14,496 cubic units, since when each linear dimension is
doubled, the volume must increase by a factor of 23, which is 8.
However, I want you to act as if you do not already know the answer to the
problem in the book. If necessary, you may copy my work below and simply
change the numbers in the appropriate places. However, you will learn more if
you read the solution and then attempt to do a complete solution to the
altered problem by subtracting the area of a small cone from the area of a
large cone.
Example solution for original
problem #21 on p. 597
Let C = center of lower base, E = center of upper base, A = apex of cone (way
up at the top—draw two dotted lines to get there), D = lower endpoint of
segment of length 6, F = upper endpoint of segment of length 6.
Drop a 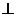 from F to from F to 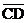 , and let J = intersection point. Then CEFJ is a rectangle,
making JD = 3. But since FD is twice as long as JD, , and let J = intersection point. Then CEFJ is a rectangle,
making JD = 3. But since FD is twice as long as JD, 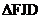 is a 30°-60°-90°
triangle. is a 30°-60°-90°
triangle.
Since 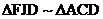 , AD must be twice as long as CD. Thus AD = 24 and AC = , AD must be twice as long as CD. Thus AD = 24 and AC = 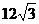 . .
Imagine the giant cone with apex A and circular base centered at C. This cone
has volume 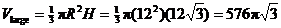 cubic units. cubic units.
Meanwhile, there is an imaginary small cone with apex A and circular base
centered at D, and we must remove this cone’s volume in order to find the
frustum’s volume (the goal of the problem). The small cone is similar to the
large one and has all dimensions in the ratio 3:4 when compared to the large
cone. Therefore, the small cone has volume 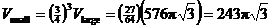 . Subtract to get . Subtract to get 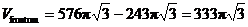 cubic units (final
answer). cubic units (final
answer).
Or, you can compute the volume of the small cone directly by using the cone
volume formula: 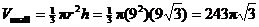 . Then subtract Vlarge
– Vsmall as above to get . Then subtract Vlarge
– Vsmall as above to get
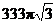 cubic units (final
answer). cubic units (final
answer).
|
|
|
Th
4/10/08
|
Test (100 pts.) on all of Chapter 12, plus §§13.1-13.3.
Optional “Immunity Challenge,” max. 4 pts., consists of showing all of
yesterday’s HW plus the following two problems: p. 621 #15, 16. If
yesterday’s assignment is sloppy or incomplete, your problems on p. 621 will
not be scored at all.
|
|
|
F
4/11/08
|
HW due: The following assignments, all previously assigned,
will be collected:
Assignment due 4/3/08: Problems in §12.6, plus #19abcdefg on small mammals.
Assignment due 4/7/08: Problems in §13.2.
Assignment due 4/8/08: Problems in §13.3 (especially #9 and #10).
Since many of these problems have already been covered in class, and since
you have no other HW due today, placeholders will not be accepted. You must
actually finish these assignments in order to earn credit. Click the archives
link at the top of the schedule if you have forgotten what the original
assignments were.
|
|
|
M
4/14/08
|
HW due: Read §13.4 (again, a review of Algebra I); write
§13.4 #2ab, 3abcd, 5a, 7a.
|
|
|
T
4/15/08
|
HW due
(will be collected Tuesday in A period, Wednesday in F period): Read §13.6; write §13.5 #1, 2, 5abcd, 9a, §13.6 #1,
2, 4, 5, 6. Hints are provided below for the §13.6 problems.
1c. General form is 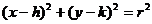 . Here, (0, –2) plays the role of (h, k), and . Here, (0, –2) plays the role of (h, k), and 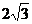 plays the role of r. Plug in to get (x – 0)2 + (y + 2)2 = plays the role of r. Plug in to get (x – 0)2 + (y + 2)2 = 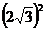 , which we simplify to x2
+ (y + 2)2 = 12. Parts
(a), (b), and (d) are very similar. , which we simplify to x2
+ (y + 2)2 = 12. Parts
(a), (b), and (d) are very similar.
2. By inspection, determine what plays the role of (h, k) and what plays
the role of r in each
equation. For example, h = k = 0 and r = 3 in part
(a). Then plot the point (h, k) as the center and sketch a circle
having radius r in each case.
4. Hint is already provided in the statement of the problem.
5a. Plug in 4 for x and 2 for y; see if the equation is a true
equation. Show your formula and plug-ins.
b. Plug in 3 for x and
–2 for y. Then proceed exactly as
in part (a).
6. You will have to invent terms for these.
|
|
|
W
4/16/08
|
HW due
(will be collected today in both A and F period): Write §13.6 #11, 12, 15. F period students will
have to teach themselves the completion-of-the-square procedure by reading
Example 3 on p. 634 and studying Mr. Hansen’s version of #11c below. (You may
copy #11c from below if you need to.) The numbers 25 and 36 that are added in
the third line of algebra can be found by a 4-step process that we call
“completing the square.”
HANDY 4-STEP GUIDE FOR COMPLETING
THE SQUARE (see example below)
1. Look at the coefficient of x
(namely, 10) or y (namely, –12).
2. Chop that in half. (That gives you 5 in the first case, or –6 in the
second.)
3. Square your result from step 2. (That gives you 25 to add to the x expression, or 36 for the y expression.)
4. Remember that whatever you add to the left side of the equation must also
be added to the right!
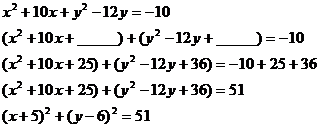
By inspection, the center is (–5, 6), and the radius is 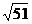 . .
If you cannot perform the factoring in the final line of algebra, you need to
see Mr. Hansen or Mr. Findler immediately for extra help. This is a basic
skill that is taught in Algebra I, and you need to be able to do it.
|
|
|
Th
4/17/08
|
HW due: Write §13.7 #1ab, 2, 5-12 all. There is no reading
assignment for today. All of these problems are based on material covered
earlier in the year.
|
|
|
F 4/18/08
|
No additional written work is due today in either
class. However, make sure you are caught up with all assignments posted
earlier in the week, since there will probably be a multi-assignment HW scan.
“A” period: After we score and go
over the recent HW, we will have a Fun Friday.
“F” period: After we score and go
over the recent HW, we will have a quiz on completion of the square and
circle sketching.
|
|
|
M
4/21/08
|
Another
quiz on circles (completion of the
square, estimating the radius, sketching).
In honor of the first really warm weekend of spring, there is no additional
written work due. However, make sure you are caught up with all previously
assigned problems.
|
|
|
T
4/22/08
|
HW due: Read §§14.1 and 14.2; write §14.1 #1, 2, 4, 5, 7,
8, 10, 18, 21, 25, 26; §14.2 #1d, 15.
Quiz (possible) on older material.
|
|
|
W
4/23/08
|
HW due: Write §14.2 #4, 5, 7, 9, 11, 12, 14, 15.
In class: Review.
|
|
|
Th
4/24/08
|
Test (100
pts.) on Chapter 13 and §14.1.
There will be a “double stuff” problem similar to problem #13 on the previous
test (bonus points if you ace it). Therefore, if you demonstrate that you
have learned from your mistakes and understand the techniques, you can earn
back some of the points you lost on the other test.
Although there is no immunity challenge this time, I strongly suggest that you do all of the following review
problems. Answers to most of them are in the back of the book. Anyone who
earns a failing score on the test will be required to show me these review
problems. Then, if the review problems are not done well, I will ask your
parents to sign a statement acknowledging that they know you (1) failed the
test and (2) did not make a reasonable effort to prepare yourself for the test.
Suggested review problems: pp. 644-646 #4-10 all, 13, 19, 21, 22.; p. 655
#27, 28. Below are the answers to the even-numbered problems.
4a. (10, 0) by inspection
b. (2, 6) by inspection
c. Since AB = 9, CD must be 9 also (prop. of parallelograms). Since
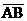 is horizontal and
since is horizontal and
since 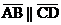 , we can conclude that , we can conclude that 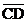 is also horizontal.
Final answer: (–4, 4). is also horizontal.
Final answer: (–4, 4).
6a. 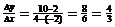
b. 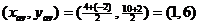
c. Use midpoint found in part (b), and connect it to point B.
Slope = 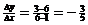 . .
d. Use distance formula: 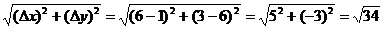 . .
e. Answer: 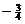 . (Take opposite reciprocal of answer to part (a).) . (Take opposite reciprocal of answer to part (a).)
f. The fact that the line is supposed to go through A is
irrelevant. Simply take the same slope as the slope of 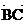 , namely , namely 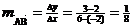 . .
g. Use same procedure as in part (e), namely the opposite
reciprocal of part (a). Answer: 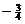 . .
8a. By direct plugging in (no work needed), equation is 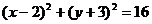 . .
b. Similarly, 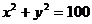 . .
c. Make a sketch showing that center is at (5, 0) and that r = 5. Answer: 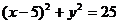 . .
10a. Convert to slope-intercept form to get 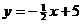 . By inspection, slope = . By inspection, slope = 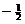 . .
b. By inspection, slope = 2.
Overall answer: The lines are 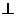 . .
22. Complete the square, as in the quizzes:
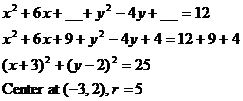
p. 655, #28. This is fun to visualize with a pencil! Watch the locus traced
by the pencil’s midpoint as the pencil slips from being flush to the wall
(vertical) to being flat on the floor, while you keep the top of the pencil
always in contact with the wall.
The locus is a quarter circle with radius 3 m and center at the point where
the wall meets the floor.
Proof: [You will need to make your own diagram.] Place the origin, point O,
at the point where the wall meets the floor. Wlog, let the ladder’s midpoint,
M, have coordinates (x, y), where  . Let L = top of ladder, P = point on the wall that is at
the same height above the floor as M, and B = base of ladder. Since OP = y, we can apply the Side Splitter
Theorem to . Let L = top of ladder, P = point on the wall that is at
the same height above the floor as M, and B = base of ladder. Since OP = y, we can apply the Side Splitter
Theorem to  and and  to conclude that PL
= y also. Note that if x and y are both nonzero, to conclude that PL
= y also. Note that if x and y are both nonzero,  is a right triangle,
allowing us to apply the Pythagorean Theorem to get is a right triangle,
allowing us to apply the Pythagorean Theorem to get 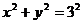 . This equation (where . This equation (where  ) is simply the equation of a quarter circle centered at O
with radius 3. The equation ) is simply the equation of a quarter circle centered at O
with radius 3. The equation 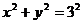 is true even if x = 0 (in which case y = 3) or if y = 0 (in which case x
= 3). (Q.E.D.) is true even if x = 0 (in which case y = 3) or if y = 0 (in which case x
= 3). (Q.E.D.)
|
|
|
F
4/25/08
|
No additional HW due. Yippee! However, older
problems may be spot-checked.
|
|
|
M
4/28/08
|
No school (Phi Beta Kappa day).
|
|
|
T
4/29/08
|
HW due (strongly recommended): Read §14.3; write §14.3 #5-10 all. Most of this is a
review of material we covered last fall. The only new material is Theorem
131, which says that the centroid is
at a point 2/3 of the way from any vertex to the midpoint of the
opposite side.
This assignment will not be collected today. However, it would be a good idea
to do as much of it as you can, since then you will have less work to do
tomorrow night.
The memory aids we learned earlier are restated below for your recollection.
PBCC: In
any triangle, the perpendicular
bisectors coincide at the circumcenter.
ABIC: In
any triangle, the angle bisectors coincide at the incenter.
ALTO: In
any triangle, the altitudes
coincide at the orthocenter.
MCCG: In
any triangle, the medians
coincide at the centroid
(which is the center of gravity if the triangle is the
base of a very thin triangular prism of uniform density).
|
|
|
W
4/30/08
|
HW due: Do one of the following, either #1 or #2 (your
choice). Note that #2 includes a project.
1. Do yesterday’s assignment if you have not already done so; then write
§14.4 #4, 19. (In §14.4 #4, make 4 separate constructions. Neatness counts.
Sloppy work or work in which the arc marks are not shown clearly will not be
accepted for grading.)
2. Do yesterday’s assignment if you have not already done so; then write
§14.4 #19 and build the following project.
Project: Using a straightedge to
make precisely straight lines, make a large triangle of random dimensions on
a thin sheet of cardboard. The backing of a legal pad would work well as a
piece of cardboard for this project. Construct all three midpoints of the
sides, taking care to show your arc marks and perpendicular bisectors.
Carefully construct the segments that connect each vertex of the triangle to
the midpoint of its opposite side. These segments should coincide at a point.
(If they do not, then start over with a fresh sheet of cardboard and work
more carefully.) What is this point called? ________________________ Write
the name of the point (one word) near its location on the cardboard. Carefully
cut your triangular region out of the cardboard. Demonstrate with a thumbtack
inserted into the point you found that your solution is correct. Bring your
completed project to school.
|
|