|
M
3/3/08
|
HW due: Read §11.5; prove Theorem 107 on p. 532. Be sure to
write the “Given” and “Prove” statements, as well as a wlog diagram. A paragraph proof is acceptable.
Hints: Let n = number of sides. Let b
represent a side of the n-gon,
which can be thought of as a base of a small isosceles triangle as depicted
in the diagram in the middle of p. 532. Let p represent the perimeter of the regular n-gon, and let A
represent the area of the regular n-gon.
Since the polygon is regular, the value for b is the same regardless of which triangle one looks at. Why does
p = nb? (That is the key to
the proof. Explain why that is true, and the rest of the proof should
follow.) Then, use the triangle area formula to develop a formula for A. Your book gives you this hint in
the sentence in the middle of p. 532 beginning with the words, “If you write
an expression . . .”
Given: Regular n-gon ABCDEFGHIJKLMN
. . . with apothem a
Prove: 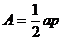
|
|
|
T
3/4/08
|
HW due: Read §11.6; write §11.5 #15, 17, §11.6 #1, 3, 4, 9,
11.
|
|
|
W
3/5/08
|
HW due: Read §11.7; write §11.6 #13, 14, 15.
|
|
|
Th
3/6/08
|
HW due: Read §11.8; write §11.7 #1, 2, 4, 6, 8, 9.
|
|
|
F
3/7/08
|
HW due: Write §11.8 #1, 2, 4, 7; p. 556 #25c, p. 557 #27ab.
|
|
|
M
3/10/08
|
HW due: Write these review problems on pp. 554-559: #1, 2,
3, 8, 9, 10, 13, 16, 17, 28, 35, 42.
In class: Review.
Watch the 3/11 calendar entry for some additional answers posted from review
problems. (These will be posted late in the evening on Monday, 3/10/08. You
may wish to check your answers after you have worked on the problems.)
|
|
|
T
3/11/08
|
Test on
Chapter 11. Internal and external
tangent procedures may also be retested, and this time, right angles must be
marked for full credit. Immunity Challenge (max. 4 pts.) consists of the
following problems: pp. 558-559 #35 (redone beautifully), 36, 38, 44.
Note: As you are reviewing your
internal and external tangent procedures, you may find the calendar entries
for 2/13/2008 (internal) and 2/19/2008 (external) to be helpful. I spent a
lot of time making those diagrams! It would cheer us both up if you could get
some benefit from them.
Answers to Selected Review Problems:
8. Diagonals are 9 dm and 5 dm, making 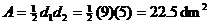 . At 3 cents per square dm, the cost is 67.5 cents.
Or, you can get the area as 2250 cm2 and convert. Since there are
10 cm in a dm, there are 100 square cm in a square dm. . At 3 cents per square dm, the cost is 67.5 cents.
Or, you can get the area as 2250 cm2 and convert. Since there are
10 cm in a dm, there are 100 square cm in a square dm.
17. Method 1 (Hero’s Formula): 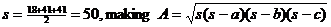 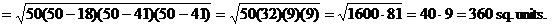
Method 2 (split isosceles triangle into 2 congruent right triangles): Each
half has legs of 9 and 40, with hypotenuse of 41, since 92 + 402
= 412. Therefore, 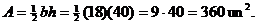
28.(a) 82:182 = 16:81 (b) 62:92
= 4:9 (c) 1:1 since triangles I and II are
similar
35. The trick is to make a square joining the centers. Since the square has
diagonal 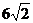 , the diameter of the large circle is , the diameter of the large circle is 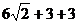 , making its radius , making its radius 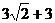 . Therefore, the large circle has area . Therefore, the large circle has area 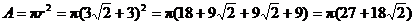 through use of
“FOIL.” Subtract 4 small circles’ area (namely, through use of
“FOIL.” Subtract 4 small circles’ area (namely, 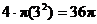 ) to get final simplified answer: ) to get final simplified answer: 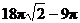 sq. units. sq. units.
36.(a) The trick is to see that each of the white slivers is a circular
segment. In other words, finding the area of the white sliver is exactly the
same as solving #27(b), except with a radius of 10 instead of 6. Multiply by
3, and subtract from the area of the large equilateral triangle.
36.(b) The trick is to see that the white area at the top of the diagram is a
circular segment. Make an auxiliary radius from the center to the point near
the top of the diagram so that you can calculate the central angle for the
circular segment. After finding the area of the segment, subtract from the
area of the upper semicircular region.
42. The trick is to find the diameter of the circle. By making a right
triangle with legs of 4 and 12, we know the diameter is 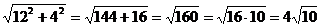 . Therefore, r = . Therefore, r = 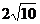 , so that , so that 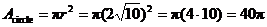 . Subtract 5 little “4 by 4” squares to get final answer: . Subtract 5 little “4 by 4” squares to get final answer: 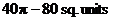 . .
|
|
|
W
3/12/08
|
HW due: Read §12.1; write §12.1 #1, 3, 5, 6, 7d, plus the problem
below.
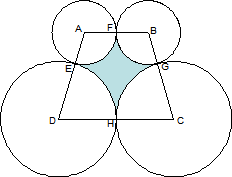
Given: Circles A, B, C, D tangent at E, F, G, H as shown
ABCD
is a trapezoid
rA = rB = 2
rC = rD = 6
Prove: 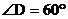
Compute: Shaded area
(Hint: Proving that 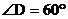 is quite helpful.
Use that fact in finding the shaded area, even if you could not prove it.) is quite helpful.
Use that fact in finding the shaded area, even if you could not prove it.)
|
|
|
Th
3/13/08
|
HW due: Read §12.2; write §12.2 #2, 4, 6, 10, 12, and
compute the approximate original lateral area of the Great Pyramid (slant
height 611 ft., s = 756 ft. for
square base).
Then do the “four circles and trapezoid” problem from yesterday if you have
not already done so. This problem requires knowing that angles C and D are 60
degrees. Use that fact (even if you are unable to prove it) to find the area
of the shaded region.
Hint: Drop perpendiculars from A
and B down to 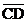 , and call the points of intersection X and Y,
respectively. Since XY = AB, you should be able to compute DX, which is the length
of the short leg in a triangle whose hypotenuse has the already known length
DA. To what family must , and call the points of intersection X and Y,
respectively. Since XY = AB, you should be able to compute DX, which is the length
of the short leg in a triangle whose hypotenuse has the already known length
DA. To what family must 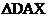 belong? belong?
|
|
|
F
3/14/08
|
(Pi Day, also the end of the third quarter)
HW due: Read §12.3; write §12.3
#1-4 all. If a clear majority of students in each section have done this
assignment well, there will be no written HW during spring break. Yippee!
Note: The “four circles and
trapezoid” problem may be collected today.
All typos, crossword puzzles, and
other extra credit of any type must be given in person to Mr. Hansen by noon
today. Late submissions, as well as submissions left in the office or in
the mailroom, will be applied toward the fourth quarter.
|
|
|
M
3/31/08
|
Classes resume.
|
|
