|
M
12/3/07
|
HW due: Read §7.2 and the exam
tips; write §7.1 #3, 4, 5, 6, 10, 12, 15, 16.
You do not need to start studying for the midterm exam yet. However, you should
be thinking about it and starting to consolidate your knowledge. If you have
never taken a comprehensive exam before, you need to know that this will
require a considerable amount of preparation. You should plan to begin
preparing for the midterm exam before
Christmas break. Please see Mr. Findler if you need help putting together a
study plan.
|
|
|
T
12/4/07
|
HW due: Read §7.3; write §7.2 #1-6 all, 8, 10, 12.
|
|
|
W
12/5/07
|
HW due: Read §7.4; write §7.3 #1, 3, 8, 10, 11, 13, 14. Remember
that it is not enough to write the answer. In many of these problems, you
must write the formula, the plug-ins, and the circled answer (with units if appropriate). In #14, you must
justify your answer.
Warning: There is a misprint in
#14(d). The word “convex” should be inserted before the word “polygon” in the
first line.
|
|
|
Th
12/6/07
|
HW due:
1. Write §7.4 #4, 5, 8, 10-13 all
2. Make sure that the word “convex” is written in ink immediately before the word “polygon” in Theorem 57 at the
bottom of p. 308.
3. (optional) Send some anonymous e-mail feedback by clicking here.
Important: When asked, please type
Stu Dent as your name and geom [at sign] modd.net as your address so that I
cannot tell who you are. If you enter a truly phony e-mail address such as
geom [at sign] stuvwxy.com, the message will not be delivered—it will simply go into the bit bucket and nobody
will ever see it again. You must use a plausible address for a real website,
such as modd.net, so that the message will be delivered to me.
What do you enjoy about our class? What do you dislike? Are audio-visual aids
(SmartBoard, chalkboard, computer videos, etc.) being used effectively? Are
you learning? Are you bored? What you would you like to tell Mr. Hansen to do
differently—or do more of? These are the kinds of things I want to know
about.
|
|
|
F
12/7/07
|
HW due: Write review problems on pp. 320-323 #2-8 even, 12,
14, 16, 26.
Class will meet at the normal time and location today for all Form III
students!
Attention, Form IV students only:
Since you may not be in class today because of the House Tour, and since some
of you were also absent yesterday because of the delayed start, it is
critical that each of you meet with me before the test. Come in during before
school today (Friday) or during A period, before you report to your House
Tour duty station. If that is impossible, then contact me at 202-537-6693 or
leave a message to set up a meeting time. The following times are open:
7:30-8:00, 8:45-10:25, 12:00-12:40.
|
|
|
M
12/10/07
|
Test (100
pts.) on Chapters 6 and 7.
Immunity challenge this time consists of the following:
pp. 289-290 #12, 13; pp. 320-323 #1, 3, 9, 10, 11, 13, 17-21 all, 25.
You should do all of these. During the test, I will randomly select two. If
both are excellently done, you will be able to protect yourself against 4
points of loss on the test; if only one problem is excellently done, 2
points. If neither of the ones that are randomly chosen is a problem that you
did well, then you still obtain a benefit (though no points), since you will
have accomplished part of your studying for the test by working on these
review problems.
Statistically speaking, even if you do only half the problems, there is still
a decent chance that you will be able to protect yourself against 2 lost
points on the test. But why not strive for doing all of them? You will be
better prepared for the test that way.
To help you with studying, two solutions are available by clicking here.
|
|
|
T
12/11/07
|
HW due: Read §8.1 and (if time permits) §8.2 as well.
Reading notes are required, as always, but there are no additional problems
due.
|
|
|
W 12/12/07
|
HW due: Write §8.1 #1, 3, 4, 6, 8, 10, 11, 14, 21, 22;
write §8.2 #1-7 all, 13, 14.
|
|
|
Th
12/13/07
|
HW due: Read §8.3; write §8.3 #1, 4, 8, 19, and finish up
any remaining problems from the previous day.
|
|
|
F
12/14/07
|
HW due: Read §8.4; write §8.4 #1-11 odd, 15. If you wish,
you may use the abbreviations SSP and SAC (pronounced “Sip Sack”) as found on
the special abbreviations page. SSP means that
sides of similar figures are in proportion, and SAC means that angles of
similar figures are congruent.
|
|
|
M
12/17/07
|
HW due: Read §8.5 carefully; write §8.3 #16 (explanations
and diagrams required), §8.4 #12, 13, 20, 21. As always, you should pay
special attention to the sample problems on pp. 352-354. (Otherwise there is
not much point in having a textbook, other than for building muscles as you
tote it up and down the wooden stairs.)
Quiz (10 pts.) is possible on the
basics of §8.5. This would be an open-notes quiz as a way of encouraging you
to take good notes.
|
|
|
T
12/18/07
|
HW due: Read §9.1 (review); write §8.5 #3, 10-14 all, 19,
20, 27. The last one is fairly challenging, but you must at least make a good
diagram for #27. In #3, prove that the diagram is impossible.
Annoying reminder: Your midterm exam in
January will cover all of Chapters 1 through 8. Start building an exam
preparation plan now!
|
|
|
W
12/19/07
|
HW due: Exam preparation plan. This must be a written plan
for at least your geometry midterm preparation, although you are encouraged
to make a comprehensive plan that includes your other classes as well. If you
need help, Mr. Findler in the STAySmart center has agreed to serve as a
resource. Your plan will be evaluated and graded based on the following
criteria:
1. Clarity. Are the objectives
clear? Is it going to be easy to tell whether you are staying on track or
falling behind in your studying plan?
2. Realism. Have you been
realistic in your plan? You haven’t said that you would spend more than 90
minutes on geometry in any single day, have you? (That is not very realistic
during vacation.) Have you spread your plan out over enough days that you
will be able to access and reinforce your long-term memory? (Cramming is of
virtually no use when you are preparing for a comprehensive exam.)
3. Thoroughness. Have you given
thought to the components that should be included in your studying? Have you
come up with some themes to focus your thoughts? Have you identified any
topics or chapters that may require extra attention? Have you identified a
source of practice problems? Have you incorporated the practice exam into your study plan?
|
|
|
Th
12/20/07
|
Quiz I (50
pts., half period) on Chapter 8
plus §9.1. The lower of the two quiz scores will be dropped, and the higher
of the two will be doubled and recorded as your Chapter 8 test score, out of a
maximum of 100 points. There is no immunity challenge this time. However, to
focus your studying, I have provided a significant portion of the quiz
content below. The numbers and the particulars of the questions will change,
of course.
1. There may be a question like #27 on p. 358. The tricky part (the place
where most students get stuck) is to realize that the distance between the
two flagpoles needs to be split into two portions, y and 100 – y, so that
they add up to 100 m. Two solutions are given below: one valid, one false.
Can you find the error in the false solution?

Attempt #1: By similar triangles, 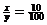 , which simplifies to a 1:10 ratio. By cross
multiplication, y = 10x. The other pair of similar triangles
gives , which simplifies to a 1:10 ratio. By cross
multiplication, y = 10x. The other pair of similar triangles
gives 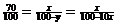 . By cross multiplication, 100x = 70(100 – 10x), or
100x = 7000 – 700x. That last equation simplifies to
800x = 7000. Divide by 800 to get x = 8.75 m. . By cross multiplication, 100x = 70(100 – 10x), or
100x = 7000 – 700x. That last equation simplifies to
800x = 7000. Divide by 800 to get x = 8.75 m.
Attempt #2: By algebra as in the previous attempt, y = 10x. By
Side-Splitter, 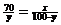 . Cross multiply to get xy
= 70(100 – y) = 7000 – 70y. Substitute for y to get x(10x) = 7000 – 70(10x), which can be rewritten to get 10x2 = 7000 – 700x.
By the quadratic formula, . Cross multiply to get xy
= 70(100 – y) = 7000 – 70y. Substitute for y to get x(10x) = 7000 – 70(10x), which can be rewritten to get 10x2 = 7000 – 700x.
By the quadratic formula, 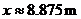 . (The negative root is discarded because lengths cannot be
negative.) . (The negative root is discarded because lengths cannot be
negative.)
2. There may be a problem similar to #3 or #4 on p. 361. If you get a problem
like #4, simplification of the radical is required. (The answer to #4 is 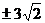 .) .)
3. There may be a problem like #5 on p. 361. The work is simple: Set up a
proportion that has x over y, and arrange the other numbers so
that the cross multiplication works out correctly.
4. There may be a problem like #11 on p. 361. Showing your work would definitely
be required. Justification (in this case, SAS~, but could also be AA~ or SSS~
in other problems) might also be required.
5. There may be a problem related to the theorem on p. 283. This is the
theorem that all 30 students missed on step 5 of the final problem of last
week’s test.
6. You may be required to give definitions for one or more of the following
terms: skew, parallel, convex, mean proportional, geometric mean, arithmetic
mean, similar, means, extremes, ratio, proportion.
7. There may be a problem testing whether you know what one or more of the
following symbols mean: 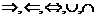 . .
8. You may have a problem similar to the side-splitter and
multiple-parallel-cut-by-transversals problems that were on the pop quiz
earlier this week. Most people did fairly well on that quiz.
9. There may be some Always/Sometimes/Never problems. However, most or all of
them will be drawn from #20 on p. 363. Explanations would be required.
Answers to #20 on p. 363 (don’t peek
until you have tried them!): AANSNAAS
Note: The answer to the last
question is N if the word “a” in #20h is replaced by the word “every”—and
since this is how I initially read this question by mistake, any student who
made the same error on the quiz will have the error marked but will have no
points deducted.
|
|
|
F
12/21/07
|
Quiz II
(50 pts., half period) on Chapter 8
plus §9.1. If you studied for yesterday’s quiz, you should not need any
significant amount of additional preparation time for today’s quiz.
|
|
