|
Th
11/1/07
|
Mastery Quiz
(10 pts.) on PBT. This will be similar to the published PBT Mastery Quiz but with a different
diagram.
The small HW assignment originally scheduled for today has been eliminated
altogether. Happy Halloween! Do remember, however, that previous HW
assignments need to be complete and should be patched up if necessary.
Everyone was provided with valid versions of #16 and #17 yesterday, for
example, meaning that those problems (at least) should now be 100% correct.
|
|
|
F
11/2/07
|
No class (teacher work
day).
|
|
|
M
11/5/07
|
HW due:
Read §5.2; write §5.1 #11, 15abc. Note that you must show work for #15b; a
simple “yes” or “no” answer will earn no credit.
|
|
|
T
11/6/07
|
IMPORTANT: Both classes will meet in Steuart 202
today.
HW due: Read §5.3; write §5.2 #2,
3, 4, 5, 6, 8.
PBT Mastery Quiz Revisited (10
pts.) for everyone, even those who passed last week. You will be required to
state the theorem and its converse in some accurate manner. Here are some diagrams that you can practice with. Make up
some random givens and try to stump your friends!
|
|
|
W
11/7/07
|
HW due:
Read §5.4; write §5.3 #3, 4, 5, 7, 10, 27.
|
|
|
Th
11/8/07
|
HW due:
Start working on your review problems/immunity challenge. I expect everyone
to be able to show a start for today
(Thursday), even though I know about your evening event with Mr. Cox. If you
bring the full set to the test Friday, you can earn a degree of immunity
against lost points.
Review problems: pp. 207-209 #6 (use PBT), 9, 16, 18; pp. 265-267 #7, 9, 11,
18, 25.
|
|
|
F
11/9/07
|
Test (100 pts.) on entire year through §5.3. Now, before you panic, please note that
only the recent material will be emphasized. However, you are responsible all
year for certain basic concepts, such as supplementary, complementary,
congruent, parallel, union, intersection, contrapositive, inverse, converse,
bwoc, wlog, and iff, to name a few. You do not need to memorize the entire
proof that 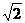 is irrational, but
you should be able to fill in the blanks if the proof is incomplete. The
first proof given in the Wikipedia article
about the square root of 2 is identical to the proof given in class. is irrational, but
you should be able to fill in the blanks if the proof is incomplete. The
first proof given in the Wikipedia article
about the square root of 2 is identical to the proof given in class.
One of the harder review problems is #25 on p. 267. Here is a mostly complete
solution:

As with all “crook problems,” the trick is to draw parallel auxiliary lines
(shown dotted above) that pass through the crook(s). Then use what you know,
usually alt. int. angle facts, to fill in the gaps. I left only a little bit
for you to finish here. All you have to do is make use of the 30° angle as an
alternate interior angle, compare against the original diagram, and you have
your answer. Do you see why we were able to split up the given 50° angle as
30° + 20°? That is an important step.
|
|
|
M
11/12/07
|
FLASH UPDATE!
The assignment listed below has been postponed until Tuesday in celebration
of the Bulldogs’ 11-7 victory over the Landon Bears in Saturday’s IAC championship
football game. If you wish to work ahead a day, you may—or you can enjoy a
pleasant weekend of relaxation and celebration.
HW due: Review your reading notes
from §5-4 (assigned last week) and reread the section if necessary. Then
write §5-4 #1, 2, 3, 8, 15, 16, 17b. Note:
For #15, you must provide a diagram, “Given” and “Prove” statements, and a
2-column proof.
|
|
|
T
11/13/07
|
HW due: No additional HW due, but make sure you have
finished the assignment listed in yesterday’s calendar entry.
|
|
|
W
11/14/07
|
HW due: Read §5.5 (reading notes optional this time); write
§5.5 #1, 3, 4, 7, 10, 11, 14.
|
|
|
Th
11/15/07
|
HW due: Read §5.6; orally prepare §5.6 #1 (do not use property numbers); write §5.6
#4, 5, 6, 8, 11, 14.
|
|
|
F
11/16/07
|
HW due: Read §5.7; write §5.7 #2, 3, 6, 8, 13, 17. Warning: Do not guess on problems 6,
13, and 17. You may want to make several sketches or even a mini-proof for
each lettered question. A significant portion of next week’s test will
consist of problems similar to problems 6, 13, and 17.
In class: Review.
The answers to §5.7 homework problems are
now posted to assist you in studying. You should also look at both the A period quiz and the F period quiz to see if you can do each one in
about 8 minutes flat. Then, grade yourself by looking at the A period answer key and the F period answer key. Scoring is 2 points for
the diagram, 2 points for listing the givens, 2 points for the “Prove”
statement, and 4 points for the proof itself.
|
|
|
M
11/19/07
|
Test on
all of Chapter 5. The immunity
challenge this time consists of pp. 264-267 #1, 2, 5, 9, 15, 19, 25, 29.
Please do your studying first . . .
and then treat these problems as if they were a practice test. Hints for each
of the problems are provided below.
1. Do not guess! Draw diagrams and make sure you understand each question.
2. Expect an algebra problem like this, or possibly one involving a quadratic
equation.
5. A technique from the beginning of the chapter is especially useful here.
9. This problem is recycled from the previous immunity challenge. Do it
again!
15. This problem is a little easier than it looks. Focus on the important
features only.
19. Do not guess! Treat these as A/S/N with explanations or mini-proofs.
25 This problem is also recycled. I want everyone to score 100% on the crook
problem.
29. Expect a proof of this difficulty, though probably a different problem.

Notes:
1. Not present for the photo was Quentin the Boring Old Quadrilateral. All of
the people you see here are related to Quentin, since they are all
quadrilaterals. They are proud of their special features, but Quentin has
none, unless you count having four straight segments all lying in the same
plane as being some sort of special feature. Also not pictured are the Skew
Quadrilaterals, which cannot be shown properly until a 3-D web page is
invented.
2. Kenny can never be a member of the Zoid clan. It is simply impossible.
(The proof, in case you are interested, is by contradiction.) However,
sometimes Kenny gets into a certain mood and stretches his triple ticks into
circles (or vice versa), at which point he becomes Rhonda. He can also become
Mr. Square if he sets his mind to it. Kenny always has the following
features: one diagonal perpendicularly bisects the other, and the diagonal
that is the perpendicular bisector is also an angle bisector. More is true,
of course, if Kenny is “in the mood” to become Rhonda or Mr. Square.
3. All squares are rhombuses, and all rhombuses are kites, but not all kites
are rhombuses.
4. Since Renny, Rhonda, and Mr. Square are all Petersons, they all have the
properties of parallelograms. Specifically, that means they all have (1)
opposite sides parallel, (2) opposite sides congruent, (3) opposite angles
congruent, (4) diagonals that bisect each other, (5) consecutive angles that
are supplementary, and (6) two sides that are both congruent and parallel.
5. Those 6 Peterson properties are also defining
properties that serve as alternative
definitions. In other words, they are “iff” conditions. To establish that
a quadrilateral is a Peterson (parallelogram), all one must do is to prove
that any of the 6 properties numbered above is satisfied. (We generally pick
whichever one is easiest to prove.)
6. Additional properties that Renny has: congruent diagonals, 4 right angles.
The second of these (namely, 4 right angles) is also a defining property of a rectangle.
7. Additional properties that Rhonda has: diagonals that perpendicularly bisect each other, diagonals that bisect Rhonda’s
angles, diagonals that create 4 congruent right triangles. All three of these
are defining properties of a
rhombus, since there is no other type of quadrilateral that has diagonals
that perpendicularly bisect each other, diagonals that bisect all angles, or
diagonals that create 4 congruent right triangles.
8. Mr. Square has a personality with all of Renny’s features as well as all
of Rhonda’s features. His diagonals create 4 right triangles that are
actually isosceles right triangles.
9. Izzy, like Renny, has congruent diagonals. In fact, Izzy is the only
member of the Zoid family with this property.
10. Quentin has a number of descendants with congruent diagonals. However,
most of those relatives with congruent diagonals are completely
undistinguished. In other words, they belong neither to the Zoid clan nor to
the Peterson clan. Even Kenny can have congruent diagonals without becoming
anything special.
|
|
|
T
11/20/07
|
HW due: Do both of the proofs below. For each one, you will
need to make your own diagram and write out the “given” and “prove”
statements before you begin. Try to do them in 2-column format. However, a
paragraph proof is acceptable if you cannot figure out how to make them work
in the 2-column format.
1. Prove that if quadrilateral ABCD has 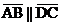 , and if , and if 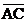 bisects bisects 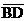 , then ABCD is not a trapezoid. , then ABCD is not a trapezoid.
2. Prove that if WXYZ is a kite, then WXYZ is not a trapezoid.
|
|
|
M
11/26/07
|
HW due: Read §6.1 (reading notes are required, as always).
If you wish to read farther ahead in Chapter 6 during your vacation, that is
OK also.
|
|
|
T 11/27/07
|
Quiz (10
pts.) on yesterday’s lecture.
HW due: Read §6.2; write the
portions of #2 and #3 that we did not do in class, plus #11, 14.
|
|
|
W
11/28/07
|
HW due: Read §6.3; write §6.1 #16, §6.2 #1, 3, 6, 10, 13.
|
|
|
Th
11/29/07
|
HW due: Write §6.3 #1, 3, 4, and the problem below.
12. A Möbius strip is a flat (i.e.,
2-dimensional) surface that twists through a third dimension in order to make
it possible to reach portions of the surface that would otherwise be
completely unreachable. For example, an ant could walk along a Möbius strip,
without ever changing sides, and yet manage to reach another ant that had
been on the “other side” of the first ant’s original starting point.
(a) How many sides does a Möbius strip really have? Give a reason for your
answer.
(b) Bring a model of a Möbius strip to class. (Take a strip of paper,
approximately half an inch wide and 10 or 11 inches long. Give it a half
twist at one end, and tape the ends together.)
(c) One possible interpretation of the fifth dimension is that it represents
all possible branching of 4-dimensional spacetime (the world we think we live
in). In the video we saw, the claim was made that the fifth dimension
collapses to actual points in our 4-dimensional spacetime through the act of observation.
If the fifth dimension could be twisted or folded through a sixth dimension
in a “Möbius-like” way, what exciting possibilities might that create? One or
two sentences will suffice. Although this is a fascinating topic, I am not
looking for a long paragraph or an essay. (Note: The possibilities go considerably beyond mere time travel.)
|
|
|
F
11/30/07
|
HW due: Read §7.1; write §6.3 #7, 9, §7.1 #1, 9.
|
|

