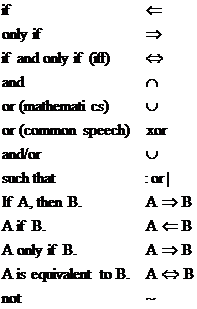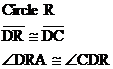Monthly Schedule

(Geometry, Periods A and F)

M 10/1/07	HW due: Read §2.6; write §2.5 #14, §2.6 #10. Observe that #14 is an algebra problem. If you cannot solve it, you need to make sure you are using all of the given information. No credit will be given for a bare placeholder with no work. Anyone who has passed Algebra I should be able to set up the equations, and if your work is careful and accurate you can get the correct answer. The “answers” to #10 are given below, but you must write everything: “Given” statements, “Prove” statement, diagram, and 2-column proof. 1. Given. 2. Given. 3. Add. prop. (statements 1, 2) 4. Given. 5. Given. 6. Mult. prop. (3, 4, 5)
T 10/2/07	HW due: Read §§2.7 and 2.8; write §2.6 #3, 6, 7, 12, 14.
W 10/3/07	HW due: Write §2.7 #4, 5, 8, 11, §2.8 #1, 9, 11. Also start working on a selection of review problems to prepare for your test. I recommend #12 and #13 on p. 106 for starters, but you may choose your own review problems for today and tomorrow.
Th 10/4/07	Test (100 points) on Chapter 2, logic puzzles, constructions, and class discussions. Since F period was not able to get to any recent homework or Chapter 2 review problems during class yesterday, I agreed to post the answers to the Chapter 2 review problems. Class discussion items will be included. For example, you need to know terms such as chaos, forward chaining, backward chaining, deduction, induction, and the various symbols we discussed, including the following:
F 10/5/07	Faculty professional day (no school).
M 10/8/07	Holiday (no school).
T 10/9/07	No additional written HW due. Please enjoy your long weekend, and get plenty of sleep!
W 10/10/07	HW due: Read §3.3; write §3.1 # 1, 2, 3, §3.2 #1, 2, 4.
Th 10/11/07	Notice: Both classes will meet in Steuart 202 today. HW due: Read §3.4; write §3.3 #2-7 all, 11. Most of #4 is done for you below as an example. (All you have to add is the diagram and the statements of the “Given” and “Prove.”)
	________________________________________________________________________
	1. T and R tris.	|  1. Given
	2.	|  2. Def tris.
	3.	|  3. Given
	4.	|  4. Given
	5.	|  5. SAS (2, 4, 3)
	6.	|  6. CPCTC
	(Q.E.D.)
F 10/12/07	HW due: Read §3.5; write §3.4 #1, 4, 6, 12, and your choice of any 2 of the following 3 construction problems: 16. We discussed the principle of MCCG (medians coincide at the center of gravity). Use your straightedge to draw a random-looking triangle. Then bisect each side and draw the 3 medians. If you do this carefully, they will coincide at the center of gravity. 17. We discussed the principle of ABIC (angle bisectors coincide at the incenter). Use your straightedge to draw a random-looking triangle. Then bisect all the angles and construct the 3 angle bisectors. If you do this carefully, they will coincide at the center of a circle nestled inside the triangle; this point is called the incenter. 18. There is also a principle of PBCC (perpendicular bisectors coincide at the circumcenter). Use your straightedge to draw a random-looking triangle. Then construct the 3 perpendicular bisectors. If you do this carefully, the perpendicular bisectors will coincide at the center of a circle that passes through the vertices of the triangle; this point is called the circumcenter.
M 10/15/07	Quiz (10 pts.): You will be given a random looking triangle and will be required to construct the circumscribed circle. This is the same as #18 from last Friday’s HW, except that you will have a time limit of 9 minutes. I calculated this by measuring the time that it took me to construct a circumcenter and the circumscribed circle, 3.5 minutes; I then doubled that time and added 2 minutes for safety. You should be in good shape if you practice at home. The Math Open Reference has an animation that shows you exactly how to do this in case you have forgotten or simply wish to review. Note that the animation shows the construction of only two perpendicular bisectors; the third one, which would cross at the same place where the first two intersect, is useful as a check on your work but is not required. HW due: Read §3.6; write §3.5 #3, 4, 7, 19-21 (the last three are printed below). You might want to put #21 on a separate page, since it will be collected. Hint: In #4, your subgoal if you are backward-chaining would be to show .
	19. Fritz P. in the “A” period class stumbled across the principle of ALTO (altitudes coincide at the orthocenter). Use your straightedge to draw a random-looking acute triangle. Then construct the 3 altitudes, which you do by dropping a perpendicular from each vertex to the opposite side. If you do this carefully, the altitudes will coincide at a point called the orthocenter.
	20. What is the only type of triangle in which the center of gravity, incenter, circumcenter, and orthocenter are all located at the same point? Roughly sketch such a triangle, showing its inscribed and circumscribed circles.
	21. Given:      Prove:
T 10/16/07	HW due: Read §3.7 and this article about Pons Asinorum carefully; write §3.6 #4, 5, 16. The written assignment is shorter than usual so that you will have plenty of time to do the reading carefully. Note: We will combine Theorem 20 and Theorem 21 into a single biconditional (“if and only if”) theorem known as the Isosceles Triangle Theorem, or ITT for short: Base angles of a triangle are congruent iff the opposite legs are congruent.
W 10/17/07	Test (100 pts.) on §§3.1–3.6, constructions, logic puzzles, and symbols from previous test. Suggested review problems: p. 162 #1, 2, 5, 7, 8, 15. Your test will be based on problems similar (though not identical) to these, plus other problems drawn from the following skill areas: MCCG (animated demonstration by the Math Open Reference project) ABIC PBCC Venn diagrams symbolic logic (transitivity, contrapositives, etc.) Algebra I mathematical symbols (and, or, not, such that, if, only if, etc.) as listed on 10/4/07 calendar entry If you do a good job on all 6 of the review problems, you can earn an immunity credit that will guard against one missed question on the test. If you wish to take advantage of this offer, submit your review problems before the test starts. Please note, a “good job” for #1 on p. 162 would include explanations, since it takes no skill at all to make 5 random Always/Sometimes/Never guesses. ALTO will not be covered on this test. For ABIC, the last step shown in the animated demonstration (namely, dropping a perpendicular from the incenter to one of the sides of the triangle in order to construct the radius) will not be required on the test. Explanations for #1abc on p. 162: (a) Sometimes. Remember, SSA is not reliable. Sometimes, a pair of triangles that satisfy SSA are congruent, and sometimes they aren’t. (b) If they are legs, then the answer is clearly Always, by SAS. But if the corresponding sides are a hypotenuse and a leg, then the answer is also Always, by HL (§3.8). Since we have not yet covered HL in §3.8, this exact question could not be given to you on the test, but it could be given in an altered form that did not require knowledge of HL. (c) Never. With an acute triangle, all three altitudes fall inside the triangle. With a right triangle, two of the altitudes coincide with the legs, and the other altitude falls inside the triangle. Even with an obtuse triangle, one of the altitudes (the one coming from the vertex of the obtuse angle) stays inside the triangle. Therefore, since we have considered all possible types of triangles, the answer to the question is Never.
Th 10/18/07	HW due: Read §3.8; write §3.7 #1, 2, 6, 8, 10, 13.
F 10/19/07	HW due: Read §4.1; write §3.8 #2, 3, 4, 5, 9, 10. There is a hint below for #3, but don’t read it unless you get stuck. Hint for #3: Draw a dotted segment from O to X.
M 10/22/07	Notice: Both classes will meet in Steuart 202 today. HW due: Read §4.2; write §4.1 #1, 2, 4, 5, 8, 10, 15.
T 10/23/07	HW due: Write 4.2 #1-6 all. You may copy #1 from the example below if you wish, but you must do #1.
	Wording adapted only slightly to match diagram: Given: Isosc. with base and median Prove: is the perpendicular bisector of Revised wording (preferred): Given: is a median Prove:
W 10/24/07	Test (100 pts.) on all of Chapter 3, plus §§4.1 and 4.2. “Immunity Challenge”: If at the start of the test you bring in the following problems, all worked neatly and completely, you can earn enough points to protect against one missed problem on the test: p. 164 #17*, 18 pp. 206-207 #1, 5, 7, 9a. * For #17, change the problem to read as follows: “Provide a paragraph proof with reasons (or, if you prefer, a 2-column proof) to show that the perimeter of is 60.” Hint for #18: Begin by looking at overlapping triangles, and prove that . This is the approximate level of difficulty that you can expect to see on the test. (The hint makes the problem reasonable.)
Th 10/25/07	No additional HW due today.
F 10/26/07	HW due: Read §4.4; write §4.4 #3, 4, 6, 12. Then, work on the PBT Mastery Quiz. Although everyone will eventually ace this quiz, it is unlikely that you will score 100% on the first try. See if you can make STA Geometry history! In class (after HW coverage): Fun Friday planned activity.
M 10/29/07	HW due: Read §4.5; write §4.4 #17, §4.5 #1, 4. Also, turn in your PBT Mastery Quiz in final form, with no mistakes. You may consult with friends, but beware! If they make any mistakes, you will be in trouble. Take responsibility for the accuracy of your own work. This quiz is fairly difficult. Hint: For #17, a paragraph proof is acceptable. This could save you a lot of time.
T 10/30/07	HW due: Read §4.6; write §4.6 #1, 2, 4, 5, 6, 8, 13.
W 10/31/07	HW due: Read §5.1; write §5.1 #1, 2, 3, 9, and the following problems. 16. The year is 2011, and you are a college student. You drive home for the weekend, and after you have been home for a while, you realize that you have misplaced your keys. You spend several minutes searching for them, at which point your ever-helpful know-it-all younger sibling says, “Gee, I’ll bet you left them in your dorm room.” How can you prove that your sibling is wrong, even if you cannot find your keys? Make a 2-column proof. 17. A prime number is defined to be a positive integer p greater than or equal to 2 such that p has no positive integers other than 1 and itself as divisors. For example, the first few prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, . . . The number 15 is not prime, because it has the positive integers 3 and 5 as divisors, in addition to 1 and 15. However, 17 is prime, because its only positive integer divisors are 1 and 17. Use an indirect proof (paragraph or 2-column, your choice) to show that the only even prime number is 2.

---

Return to the Geometry Zone

Return to Mr. Hansen’s home page

Return to Mathematics Department home page

Return to St. Albans home page

Last updated: 10 Nov 2007