|
W
9/5/07
|
First day of school.
|
|
|
Th
9/6/07
|
Quiz on
the alphabet and Greek letters alpha, beta, pi, phi (pronounced “fee”), and
theta. Click here for the study guide.
|
|
|
F
9/7/07
|
HW due:
Read §1.1; write §1.1 #1-5 all, 11. Follow the “HW guidelines” link to see
exactly what is expected from you in terms of homework.
Reading notes may be very brief, but they should include any questions that
you may wish to ask. Every time you make reading notes, try to write at least
one question that you can ask later. If you organize your questions in this
way, you can get them answered efficiently whenever you see me or one of your
classmates who might be willing to provide help. Sometimes the very act of
writing out a question will help you understand more than you did before.
Incidentally, “I don’t understand” is not a question. Be sure to write
something that actually is a question. Here is an example: What is the difference between 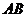 and and 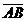 ? How do I know which style to use? ? How do I know which style to use?
|
|
|
M
9/10/07
|
HW due:
1. Patch up any discrepancies you may have had in the HW due last Friday. For
example, you may have forgotten your reading notes, you may have forgotten some
diagrams, or you may have omitted a problem by mistake. If the problem was a
formatting error, correct it if possible. If your assignment was on the wrong
type of paper, you should 3-hole-punch the paper you did the assignment on
and place it in your 3-ring binder.
2. Prepare all your equipment for our first equipment check. You will need a
pencil, a straightedge, your textbook, and a 3-ring binder at a minimum. Your
L.A. is always desired, too.
3. Read §1.2; write §1.2 #1, 2, 4, 5, 8, 9. Remember, if you cannot solve all
of a problem (for example, #9 is somewhat challenging), you need to make a
diagram as a placeholder. Make your diagrams carefully enough that they can
be useful in solving the problem.
|
|
|
T
9/11/07
|
HW due:
1. Read §1.3 (reading notes required, as always)
2. Write §1.3 #1, 3, 7, 8.
3. Write the following spelling words at the end of your homework paper:
collinear, theorem, parallelogram, trapezoid, rhombus, perpendicular.
|
|
|
W
9/12/07
|
HW due:
Read §1.4; write §1.4 #3, 7 using the format we discussed in class. Be sure
to put the Halmos sign or Q.E.D. at the end.
|
|
|
Th
9/13/07
|
HW due:
Read §1.5; write §1.4 #6, 9, §1.5 #1, 2, 3, 4abc, 5, 7, 8.
Note: In #5, the figure shown is
supposed to be a portion of the real number line.
|
|
|
F
9/14/07
|
HW due:
Read §1.6, especially the definition of counterexample
on p. 37; write §1.6 #1, 2, 3, 5, 7, 8; think about #10.
Warning: At least one of these is a
trick question with a conclusion that cannot be proved.
Problem #10 is the first example we have seen of a non-obvious conclusion, since most students would not immediately
understand why ĐCAE must be a right angle. Hint:
Geometry and algebra can work together to solve this problem.
|
|
|
M
9/17/07
|
HW due: Read
§1.7; write §1.7 #1-5 all, 10, 14.
|
|
|
T
9/18/07
|
HW due:
Read §1.8; write §1.8 #1-5 all.
|
|
|
W
9/19/07
|
HW due:
Write §1.8 #6, 8, 9; write review problems (pp. 54-59) #1, 3, 7, 11, 21, 23,
26, 36. If you do not finish all of the review problems, make sure you have
placeholders for all of them, and finish up the last few tonight as you study
for your test.
|
|
|
Th
9/20/07
|
Test (100 points) on §§1.1-1.8 and all material
discussed in class.
A practice test is available to
help you prepare. If you would like the answer key, please send Mr. Hansen an
e-mail message with your name (very
important, since many addresses are meaningless by themselves) and a statement of effort. My reason for not
posting the answer key or sending it out indiscriminately is that I want you
to try working the problems first, under time pressure. Otherwise you might
as well simply choose additional review problems in the textbook.
Mr. Hansen’s e-mail address is available on the contact
information page.
If you do not receive a reply, your message was probably snagged by the
Cathedral’s spam filter. Try again with a double underscore ( __ ) at the
beginning of your subject line.
By now it should be no mystery to you that the following problem categories
are highly likely to be included on the test: clock problems, addition and
subtraction of degrees/minutes/seconds, A/S/N problems,
converse/inverse/contrapositive problems, some algebra review (e.g., #36 on
p. 59), and one or two short proofs. You need to know the difference between Č (union) and Ç (intersection), the meaning of Ć (null set), and the reason that the null set is not
normally enclosed within braces. (Answer: Ć means null set all by itself. There is no need to
put braces around it when you are talking about a set of points or a solution
set.)
|
|
|
F
9/21/07
|
HW due: Read
§1.9; write §1.9 #1-8 all, 10, 11.
|
|
|
M
9/24/07
|
HW due:
1. Purchase a compass and a straightedge, if you do not already own them.
2. Bring them to class. If you forget a straightedge, you may use the edge of
your book.
3. Read and practice the following techniques:
We will discuss the techniques, but you will need to have visited the three
Web links beforehand so that you are not seeing everything for the first
time.
|
|
|
T
9/25/07
|
HW due: Read
§2.1; write §2.1 #3-6 all, 8-11 all. Challenge problem (optional): Describe
how to construct a line parallel to any given line, through a given point not
on that line. You may wish to consult a Web or library source if you cannot
figure it out on your own.
Note: There may be a short quiz
today on one or more of the construction techniques. You must show your arc
marks, and neatness counts.
|
|
|
W
9/26/07
|
HW due:
Read §2.2; write §2.2 #4, 5, 6, 11, 13, 16.
Quiz on the 4 construction
techniques. You will be required to bisect an angle, drop or erect a
perpendicular, construct the perpendicular bisector of a segment, and construct a parallel
line (namely, parallel to a given line and passing through a given point
P). The time limit is 8 minutes. You might want to practice to make sure that
you can do all 4 in under 8 minutes.
Note: The parallel line
construction link provided above by the Math Open Reference Project
differs slightly from the technique I taught you yesterday. Here are the
differences:
- In their step 2, they recommend using a radius
of “about half of RJ.” Our method was to use the full radius RJ.
Although both methods are equally valid, our method avoids any possible
confusion later about how large the second compass setting should be or
what point it should be measured from.
- Therefore, in step 4, we would use the compass
as a divider to measure the distance from point R to the unmarked point that is between their J and Q. They
have an extra point between J and R that we simply avoid by using the
first setting as RJ as described above.
- Also, in step 4, our method requires showing
the extra arc mark at the point between J and Q. They left that out, but
it is an important step for the sake of showing your work.
If you prefer to use the method shown in the Math Open Reference Project
link, I will accept it for full credit, as long as you remember to show your
extra arc mark at the point between their J and their R.
|
|
|
Th
9/27/07
|
Optional Re-Test, 7:00 a.m., Steuart Building Room
202. I am expecting the people who
failed the test (score below 70%) to be there along with the 4 other students
who signed up. If you are planning to come, be sure to let me know by 12:01
a.m. today (one minute after midnight) so that I know how many copies to
make. If you do better on the re-test than on your original test, the re-test
score will count. If you do worse, the re-test will be ignored. The re-test,
as compared to the original test, will have slightly fewer problems but will
be somewhat more difficult.
Important Notice: Period A will meet in Steuart 202 today. The reason is
that Mr. Graham is using our regular classroom for period A. Period F is not
affected.
HW due: Read §§2.3 and 2.4; write §2.3 #2, 3, 6, 10, §2.4 #1, 4, 5, 6.
|
|
|
F
9/28/07
|
HW due:
Read §2.5; write §2.5 #1-7 all, 9, 10. Note:
If you wish, you may abbreviate the addition and subtraction properties on
the “reasons” side of your two-column proofs as follows:
Add. prop.
Subtr. prop.
|
|