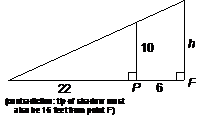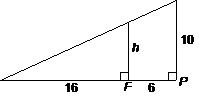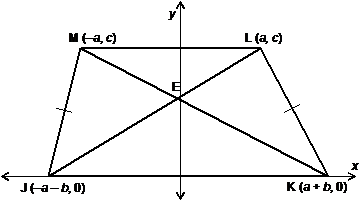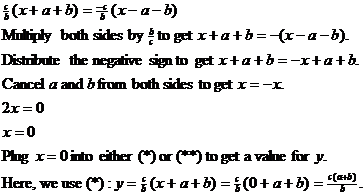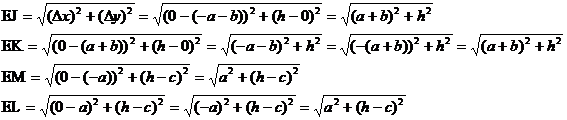|
1.
|
Let F be the personís foot, P
the base of the post. Note that the following arrangement is not possible, since if we place the
tip of the shadow 22 feet from point P
as required, then it will not be 16 feet from F.
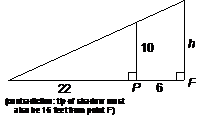
By reversing the position of the person and the lamppost, we obtain the
following diagram that meets all the conditions of the problem:
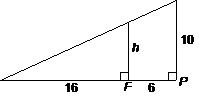
Therefore, we work from the second diagram and use similar triangles to write
proportions.
WRONG (common student error): 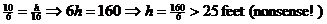
This is nonsense, not only because people taller than 25 feet are never seen
in real life, but also because the proportion 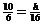 †is utterly invalid. The proportion rests on the
assumption of similar triangles, but the student has failed to use corresponding
legs of similar triangles. The leg of the larger triangle that should be used
in the proportion is 22, not 6. Although †is utterly invalid. The proportion rests on the
assumption of similar triangles, but the student has failed to use corresponding
legs of similar triangles. The leg of the larger triangle that should be used
in the proportion is 22, not 6. Although 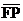 †has a length of 6, †has a length of 6, 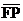 †is not a leg of any
triangle. †is not a leg of any
triangle.
Now, there is a theorem called the Side-Splitter Theorem that allows
proportions to be made involving split parts of legs, but that theorem works
only when both legs are being split. Since the legs having lengths h and 10 are not being split, the
Side-Splitter Theorem cannot be used here.
CORRECT METHOD: 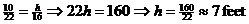
This is a very tall person, but at least the mathematical setup makes sense.
As discussed above, it is not possible to interchange the positions of points
F and P in order to get a fundamentally different diagram. (If we did
interchange F and P, then the sun would also have to be
switched so that the shadow tip was in the correct position. That would give
a diagram that might look like the mirror image of the second diagram above,
but the similar triangles and proportions would not change at all.)
BEST ANSWER: (C)
|
|
2.
|
Let 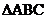 †(wlog)
be any triangle lying in plane m.
By PBT [first semester, but we canít forget it!], we know that †(wlog)
be any triangle lying in plane m.
By PBT [first semester, but we canít forget it!], we know that
(1) the locus of points in m that are
equidistant from A and B is the 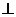 †bisector of †bisector of 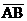 , ,
and
(2) the locus of points in m that
are equidistant from B and C is the 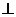 †bisector of †bisector of 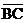 . .
Let L1 = locus from step
(1), L2 = locus from
step (2). Both loci are lines.
Is it possible to have L1
|| L2? By what we know
about || and 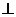 †lines, that could
happen only if †lines, that could
happen only if 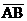 †and †and 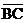 †were either parallel
or collinear. [This statement does not require proof, since only an
explanation of a process was required, not a formal proof. Think about it:
the †were either parallel
or collinear. [This statement does not require proof, since only an
explanation of a process was required, not a formal proof. Think about it:
the 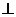 †bisectors of ||
segments may be ||, and the †bisectors of ||
segments may be ||, and the 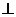 †bisectors of
collinear segments may be ||, but for any other situations, it is not
possible for the †bisectors of
collinear segments may be ||, but for any other situations, it is not
possible for the 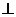 †bisectors to be ||.] †bisectors to be ||.]
Therefore, we conclude that L1
and L2 are not parallel.
But they cannot be skew either (since by steps (1) and (2), both loci lie in
plane m). Therefore, L1 and L2 either must be the same line (which is nonsense,
since that would violate the definition of 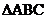 ) or must intersect at a point P. ) or must intersect at a point P.
The only possibility that makes sense is that L1 and L2
intersect at some point P. Now
consider what we know about P.
Since P is in L1 (locus
1), P is equidistant from A and B.
Since P is in L2 (locus
2), P is equidistant from B and C.
Therefore, P is equidistant from A, B, and C. Call this common distance r.
Place the point of a compass at P and set the radius to r. The compass opening is guaranteed to be the correct distance
to make a circle passing through A, B, and C, since P is at distance r from all three points. We call P the
circumcenter of 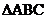 . .
[Note: If this problem were to
appear on the exam, you would not need so much detail in order to earn full
credit. For full credit, you would need to write steps (1) and (2) as shown
above, claim (without proof) that the 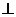 †bisectors intersect
at a point P, and write the final two paragraphs as shown. A sketch
suggesting that the †bisectors intersect
at a point P, and write the final two paragraphs as shown. A sketch
suggesting that the 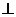 †bisectors intersect
at some P would also suffice, provided that you explained why P fulfills the
requirements of being the circumcenter.] †bisectors intersect
at some P would also suffice, provided that you explained why P fulfills the
requirements of being the circumcenter.]
|
|
3.
|
[Wlog,
place the longer base of trapezoid JKLM on the x-axis and mark coordinates as shown. Note that this diagram uses
the hint concerning equal protrusions of the longer base on each side. Also
note that it is not necessary to make the sketch precisely accurate. It can
be proved that the diagonals must cross on the y-axis, but there is nothing wrong with making the crossing point
miss the y-axis slightly, as it
does here.]
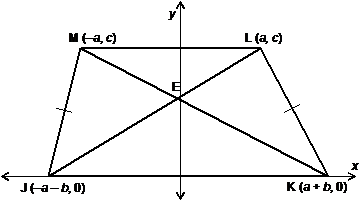
[The distance formula is probably our most basic tool in coordinate geometry
proofs. However, using the distance formula to prove that EJ = EK and EM = EL
(our goal) requires knowing the coordinates of point E. True, you could do
the proof with techniques from the first semester, but you would not
earn much credit. A first-semester approach would be to prove triangles JML
and KLM congruent by SSS (taking advantage of the fact that diagonals of an
isosceles trapezoid are congruent), 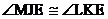 †by CPCTC, †by CPCTC, 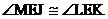 †by vertical angles, †by vertical angles, 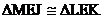 †by AAS, and finally
EJ = EK and EM = EL (our goal) by CPCTC. If you do all of that, you will have
a valid proof, but since it is not a coordinate
geometry proof, the number of points earned on the final exam would be
minimal.] †by AAS, and finally
EJ = EK and EM = EL (our goal) by CPCTC. If you do all of that, you will have
a valid proof, but since it is not a coordinate
geometry proof, the number of points earned on the final exam would be
minimal.]
[This is a wonderful review problem because it touches on almost everything
you need to know regarding coordinate geometry, lines, equations, and systems
of equations. It is somewhat longer than a real exam problem, but you can and
should work through all the steps as part of your study and review process.]
[To find E, we need to write equations of 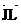 †and †and
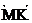 , and then we need to use techniques from Algebra I to see
where those lines intersect. Our basic tool for finding equations of lines is
the point-slope formula, which you
might need to review.] , and then we need to use techniques from Algebra I to see
where those lines intersect. Our basic tool for finding equations of lines is
the point-slope formula, which you
might need to review.]
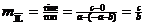
Point-slope equation of 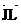 , using J to give known values of x and y: , using J to give known values of x and y:
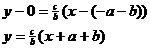
Let us refer to the simplified equation of  , namely , namely 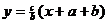 , as (*). , as (*).
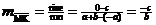
Point-slope equation of  , using K to give known values of x and y: , using K to give known values of x and y:
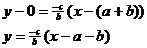
Let us refer to the simplified equation of  , namely , namely 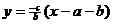 , as (**). , as (**).
At point E, both equations are satisfied. Therefore, we can set (*) and (**)
equal to each other and solve for x
as follows:
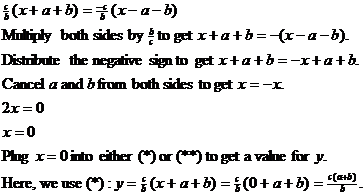
Therefore, the coordinates of E are 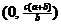 . Because the y
coordinate is somewhat messy, let us let . Because the y
coordinate is somewhat messy, let us let 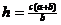 . .
Now, apply the distance formula to compute EJ, EK, EM, and EL.
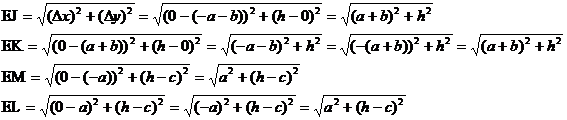
[Note that it would be an error to try to simplify the answers for EJ, EK,
EM, and EL any further.]
Since EJ = EK and EM = EL, triangles EJK and EML are isosceles as claimed.
(Q.E.D.)
|