|
6.
|
I have a die that I think
may be unfair with regard to the probability of rolling a 6. In 100 rolls I
obtain 14 sixes. Is there evidence that the die is unfair? Perform a
significance test (all 7 steps). You do not need to show your work in the
calculation of the test statistic and P-value.
|
|
|
|
|
|
Let p = true prob. of rolling a 6
H0: p = 1/6
Ha: p ¹ 1/6 (two-tailed test)
Assumptions: SRS + 3 rules of thumb [Note:
You must state and check assumptions in writing.]
SRS? Not really, but treat the trials as coming from an SRS
of all possible rolls with this die. ü
N = infinite, so N ³ 10n is
satisfied. ü
np
» 14 ³ 10 ü
nq
» 86 ³ 10 ü
|
|
|
|
|
|
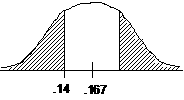
Sampling distrib. of 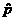 , assuming H0
true:
|
|
|
|
|
|
Test statistic: z = –0.7155 by calc.
P = 0.474
Conclusion: There is no evidence (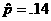 , n = 100, z = –.7155, P = .474) that the true probability of rolling a 6 differs from
1/6.
|
|
|
|
|
7.
|
[Note: For an interval, we use a different value for s.e. based on the best information we have. In other
words, it was fine in #6 to estimate
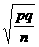
by taking p = 1/6, q = 5/6, since that made sense for a
sampling distribution that assumed the truth of H0. However, now that we are computing a C.I., we must
take p » .14, q » .86.]
We get s.e. =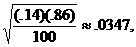 
so that m.o.e. = (z*)(s.e.) =
1.645(.0347) = .057. Answer: We are 90% confident that the true
probability of rolling a 6 is .14 ± .057, i.e., somewhere in the interval (.0829,
.1971).
|
|
|
|
|
8.
|
The commonly quoted
distribution for American men’s heights is N(69, 3) in inches. I feel that
the mean is actually higher than 69 inches, and I find an
SRS of 29 American men who agree to be measured. Their mean height is
70.2 inches, with a standard deviation of 4.1 inches. Is there evidence that
the mean of American men’s heights exceeds 69 inches? Perform all 7 steps of
the statistical significance testing process. You do not need to show your
work for the calculation of the test statistic and P-value.
Let m = true mean height of
American men
H0: m = 69
Ha: m > 69 (one-tailed test)
Assumptions: SRS, normal pop., unknown s.
SRS? Given. ü
Normal pop.? Certainly reasonable, since growth is a
natural process and is the result of a vast number of small random inputs.
However, by guidelines [see p. 606], n ³ 15 makes the normality of the population moot
unless we have outliers or strong skewness. Also, we
are close enough to the “large sample” condition of 40 that we can proceed safely, even if there is an outlier or some skewness. Bottom line: The sampling distribution of 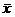 is close to a t distribution with df = 28.
Sample s.d. is given, but pop. s.d. is unknown. ü
|
|
|
|
|
|
Sampling distrib. of 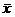, assuming H0
true:
|
|
|
|
|
|
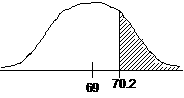
Test statistic: t = 1.576 by calc.
P = 0.063
Conclusion: There is weak evidence [or you could say, “There is no evidence .
. .”] that the true mean height of American men exceeds 69 inches (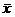 = 70.2, df = 28, t =
1.576, P = 0.063).
|
|
|
|
|
8.(alt.)
|
An alternate method of
doing #8 is to compute the 95% C.I. for m and show that 69 lies in that interval, i.e., that
69 is one of the reasonably likely values for the true population mean. If 69
is a reasonably likely value, then we cannot say that we have found evidence
for the claim that m ¹ 69,
let alone for the easier-to-satisfy claim that m > 69.
Steps:
s.e. =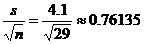 
m.o.e. = (t*)(s.e.) =
2.048(0.76135) » 1.5592 [Note: We use the t table with df
= 29 – 1 = 28.]
C.I. = est. ± m.o.e. = 70.2 ± 1.5592 = (68.64, 71.76)
Therefore, 69 is within the interval of likely values. We
cannot support the claim that m ¹ 69, and since we cannot support that claim, we certainly cannot support the claim that m > 69. (Remember, it is easier—i.e., requires
less extreme test statistics—to satisfy a one-tailed alternative hypothesis
than it is to satisfy a two-tailed alternative hypothesis.)
Arguments based on confidence intervals, as in this example, are two-tailed
by nature. However, often it is possible to make a conclusion to support a
one-tailed test.
|