|
M 1/1/07
|
New Year’s Day (no school).
|
|
|
T 1/2/07
|
Cathedral funeral for former President Gerald R.
Ford (no school).
|
|
|
W 1/3/07
|
Supplemental Formulas: Remember that several useful formulas are missing
from the AP formula sheet. Here are some that come immediately to mind:
- z = (x
– m)/s
- General Intersection Rule, always true: P(A Ç B) =
P(A) · P(B | A)
- Modified form of General Union Rule: P(A Ç B) =
P(A) + P(B) – P(A È B)
- residual = y
– yhat
- Empirical Rule: 68% of normal data are in
interval m ± s,
95% in m ± 2s, 99.7% in m ± 3s
HW due
(strongly suggested): Review for
your midterm exam, including reviewing not only the AP formula sheets
published in the Barron’s review book, but also the supplemental formulas
shown above. After you have spent several hours reviewing, preferably spread
over a period of several days, please attempt the following questions, which
together would make a fairly good sample midterm exam:
· LRSL questions
· Experimental design questions, plus more
on LSRL/curve fitting
· Conditional probability questions
· Additional sample midterm practice
questions.
We will spend some time in class discussing some of the answers to these sets
of questions. A comprehensive answer
key for the second set is available, but please do not peek at the
answers until you have tested yourself under pressure. (You will not learn
very much simply by peeking at the answers. You really need to study first,
then test yourself, then check answers.)
Warning: Every year there are some
students who think they can take a shortcut by skipping the review and
immediately taking the practice midterm exam. This is not a good idea,
because the practice exam is not comprehensive. (Think about it. There is no
way to cram a comprehensive exam into an hour and a half or two hours. We
have covered a huge amount of material since September.) Therefore, if you
take the practice exam and then go back to “plug the gaps,” so to speak, you
will not have made a comprehensive review of the material that is fair game
for the real exam. Plus, since you would have already taken the practice
exam, you would no longer have a valid way to gauge how well prepared you
are.
The bottom line is this: Study first, and then take the practice midterm exam
as a way of testing yourself. What do you do if you need more practice
questions? Simply pick questions randomly from the Barron’s review book.
|
|
|
Th 1/4/07
|
HW due:
Review all 4 links from yesterday’s calendar entry, especially the fourth one
(write out all answers to the practice questions). The more preparation you do
now, the better your midterm exam will work out for you.
|
|
|
F 1/5/07
|
HW due: Continue midterm preparation as described in the
1/3 and 1/4 calendar entries. The review problems will be spot-checked or
graded a second time.
Assembly period: You are encouraged
to come to Room R between 9:15 a.m. and 9:30 a.m. to ask any questions you
may have regarding the midterm exam. Please do not ask about the format,
which will be drawn primarily from sample questions of the type found in the
Barron’s review book. A formula sheet like the one in the Barron’s book will
be provided, but of course there are also several useful formulas (see 1/3
calendar entry) that are not provided. You may use your calculator throughout
the exam, and anything stored on your calculator is permitted.
|
|
|
T 1/9/07
|
Midterm
Exam, Room R, 8–10 a.m. The
originally published schedule said “New Dorm Room,” but that was before we
realized that we would not yet be moving out of Room R.
|
|
|
W 1/10/07
|
Conflict
Exam for Kellie and Marcus, Room R, 11 a.m. –1 p.m.
|
|
|
W 1/17/07
|
Classes resume.
|
|
|
Th 1/18/07
|
HW due: Write #7.8, #7.15; read pp. 385-394, including the
examples but omitting the exercises (8 pages altogether); write #7.22.
|
|
|
F 1/19/07
|
HW due: Read pp. 395-406, again including the examples but
omitting the exercises; then write the following exercise taken from class.
Let X = payoff to you when playing
the unfair die-rolling game given in class. (You win $1 if a 1 is rolled, you
win $2 if a 2 is rolled, but you lose $3 if a 3 or 4 is rolled. No money
changes hands if a 5 or 6 is rolled.)
1. Compute mX, showing your work. This should already be in your
notes.
2. What alternate name and notation are used for mX?
3. We found in class that the errors (deviations from the mean) were 1.50,
2.50, –2.50, and .50. Explain how we found each of these values.
4. Compute the mean squared error. When we say “mean,” we mean a weighted
average computed by using the probabilities as weights. In other words, weight
the 1.502 by 1/6, the 2.502 by 1/6, and so on.
5. What is the more customary name that we use for MSE?
6. Use both of the notations given
in class to state your answer to #4.
|
|
|
M 1/22/07
|
HW due: Read pp. 415-423; write #7.34, 7.35, 7.43, 7.44,
and the following problems:
Let X be the height of a randomly
selected STA Upper Schooler. Suppose that X
follows the N(71, 3) distribution.
Let Y be the height of a randomly
selected NCS Upper Schooler, and suppose that Y follows the N(67,
2.5) distribution.
1. What does Z = X – Y represent?
2. Compute mZ and sZ, showing your work and using correct notation. You
will find Friday’s class discussion invaluable here.
3. What would it mean (in words) to say that Z > 0? Be sure to use the context of STA and NCS in your
answer.
4. What distribution does Z follow?
5. Compute (a) P(Z > 0) and (b) P(Z £ –1).
6. Write, in English, what each of your answers to #5 represents. Be sure to
use the context of STA and NCS in your answers.
|
|
|
T 1/23/07
|
HW due: Read pp. 424-433; write #8.20, 8.22. Hint: Use #8.19 and 8.21 as guides. Of
course, you need to show more work than is shown in the answer key.
For example, answer key may say sX = 1.386
without any real explanation. For full credit, you must write formula, plug-ins, and answer with
units. Example for #8.22(c):
Let X = # of 12 truthful persons
who will be classified as deceptive, p
= 0.2, q = 0.8, n = 12.
mX = np
= 12(0.2) = 2.4 people (i.e., we expect between 2 and 3 people to be
doubted);
sX = 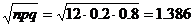 people. people.
|
|
|
W 1/24/07
|
HW due: Read pp. 434-444 plus the chapter review on pp.
446-447; write #8.39, 8.44abc. If your eyes glaze over when you read all the algebra
on p. 442, you have my permission to skip it. However, you may wish to take a
stab at the following 1-point bonus question:
1. Give a proof of the statement in the box at the bottom of p. 442 that uses
no algebra.
|
|
|
Th 1/25/07
|
HW due: Read pp. 456-463 twice; write #8.37, 8.41 (part h
is optional).
The definition on p. 459 is the most subtle and important definition of the
entire second semester. See if you can rephrase it in your own words.
|
|
|
F 1/26/07
|
HW due: Read pp. 463-469; write #9.11.
Note: Keystrokes to start creating
the program are shown below.
PRGM New 1 SHOPPER Enter
You should now have a colon (“:”) prompt. Enter the program exactly as shown,
and press 2nd QUIT when finished. Execute the program with PRGM EXEC.
If you have trouble locating some of the commands, such as ClrHome or cumSum
or Disp, please remember that 2nd CATALOG lists all possible commands in
alphabetical order. Since ALPHA LOCK is enabled when you enter 2nd CATALOG,
you need only press the letter of the desired command (e.g., C for ClrHome)
in order to skip forward to the commands that start with that letter.
|
|
|
M 1/29/07
|
HW due:
1. On last year’s test, work all of
Part I (including the example), plus questions #7-16.
2. Answer questions #9.9 and 9.10 on pp. 468-469.
|
|
|
T 1/30/07
|
Test on Chapters 7 and 8, plus the following
topics:
- Nominal, ordinal, interval (arithmetic), and
ratio scales
- Definition of sampling distribution
- Definition of bias
- Definition of sampling error (sampling
variability)
- Rough conception of how sampling variability
decreases as the size of the SRS grows (but note: population size
generally does not matter)
- Finally, as we discussed in class, you cannot
forget your probability knowledge, since some of the questions may
require you to calculate probabilities other than binomial or geometric
probabilities.
|
|
|
W 1/31/07
|
HW due: Write up all of yesterday’s
test, regardless of whether or not you took it, and regardless of whether
or not you think you already answered certain portions correctly. You may
write directly on the test paper.
Note: This time, you must show work
on problems 9, 10, and 11. You may compare answers with classmates, and you
may work together to discuss solution strategies. However, you may not copy.
Your submission must be completely your own.
The results of the test, especially problem 6, were so dismal that I am contemplating
throwing the entire test out and holding a re-test in which the maximum score
is 80%. We will revisit this issue in class and decide what to do. I may be
persuaded to back down from my position if the overnight re-do of the test is
impressively done.
Here are the results for problem 6, which (remember) was a recycled homework
question. Instead of STA and NCS, we had Glermans and Drench. Instead of
height, we had weight. Surely this was not an unfair question.
# of students who suggested a Monte Carlo approach (partial credit): 2
# of students who knew enough to define a random variable Z = G – D: 2
# of students with no clue whatsoever: 8
|
|