|
W 11/1/06
|
HW due: Each group will turn in 5 or 6 of the best of the best questions that would
make a good survey. Peter, who was absent on 10/31, should refine the 10/31 assignment,
adding at least one question.
|
|
|
Th 11/2/06
|
HW due: Read pp. 245-265. Reading notes are required (as
always).
After HW check: “Fun Friday on Thursday” per Kellie’s choice.
|
|
|
F 11/3/06
|
No
school.
|
|
|
M 11/6/06
|
HW due: Read pp. 265-276. You need not read the exercises,
which means that this is really only 9 pages of reading. However, do read the examples (e.g., Example
5.10 on pp. 269-270).
The quiz originally scheduled for today has been moved to tomorrow.
|
|
|
T 11/7/06
|
Quiz (10 pts.) will allow full use of notes but not the textbook.
In class: Review.
|
|
|
W 11/8/06
|
Quest (70
pts.), Version 1 (no written notes allowed). This will focus on recent material but will contain
some cumulative problems going back to the beginning of the year. All
questions will be short answer or multiple choice.
|
|
|
Th 11/9/06
|
Quest (70
pts.), Version 2 (no written notes allowed). This will be similar to yesterday’s version and
will occur during the second half of the period. Students who did well
yesterday will have some free time.
Study aids: Blank copy of Version 1, answer key for Version 1, blank copy of Version 2, answer key for Version 2.
|
|
|
F 11/10/06
|
Quest (70
pts.), Version 3 (1-pg. handwritten study sheet allowed; Quick Study will
be covered). This optional quest
will be given at 7:00 a.m. in Room R, although you may arrive as late as 7:15
without penalty. This is the one and only make-up opportunity for people who
missed Wednesday and Thursday. If you take the quest more than once, the best
score will count.
HW due: Read pp. 277-296,
including the examples and summaries but omitting the exercises. That is a
total of about 14 pages of reading.
|
|
|
M 11/13/06
|
HW due: pp. 296-297 #5.60, 5.62. Use a chart similar to my example to record your results for #5.62.
Copy the headings and the first detail row exactly as shown in the example,
but use your random integer generator to fill in the remaining rows. (Do not
copy the results that I obtained.)
Additional HW for people who were
absent Friday or who were unable to complete the in-class exercise:
Answer all of the Quest Version 3 questions
correctly. You do not need to use a bubble sheet. Be prepared for an oral
quiz to verify that you actually understand the reasoning behind each answer.
The scoring is binary: full credit if your answers are 100% correct, no
credit otherwise.
|
|
|
T 11/14/06
|
HW due:
1. Write #5.64. If you use a calculator to automate the process, provide a
written program listing. Run at least 100 trials of 3 numbers each.
2. Disease X affects 0.5% of the people you might meet randomly on the street
(i.e., 1 person in 200). If you select 160 people at random, what is the
probability that at least one of them has Disease X? Show your work or
perform a simulation. (Preferably, do both.)
|
|
|
W 11/15/06
|
HW due: Read Chapter Review (pp. 298-300); write #5.68,
5.70, 5.72, 5.80.
Note: In #5.80(b), we will combine
results in class. However, note that you are to perform 20 repetitions of 20
simulated free throws, i.e., 400 free throws in all. Clearly, a calculator is
much handier than the random digit table, but since the AP exam requires you
to use a random digit table, you need to demonstrate the ability to do that
for at least 1 simulated group of 20 free throws. (Record your digit
assignment method and the random digits that you obtained.) For the others,
you may use the following calculator program:
:ClrHome
:0®S
:For(J,1,20,1)
:rand®X
:If X<.8
:Then
:"B"®Str1
:S+1®S
:Else
:"-"®Str1
:End
:Output(1+int(J/11),J-int(J/11)*10,Str1)
:End
:Output(3,1,S)
:Output(3,4,"BASKETS MADE")
The ClrHome command is found under the PRGM I/O menu. The int function is
found under 2nd CATALOG. The Str1 variable is entered with keystrokes VARS 7
1.
Translation into plain English: This program generates 20 random free throws
(i.e., a single repetition of the simulation). You will need to run the
program 19 or 20 times in order to gather enough data for merging with
everyone else’s data. For each repetition, record the longest streak of B’s
in a row that you see. (The total number of baskets made is somewhat
interesting but irrelevant, since this exercise is concerned with streaks.)
|
|
|
Th 11/16/06
|
HW due: Read this
article that gives a preview of an article that will be released (probably
to some media fanfare) later this week in JAMA,
the Journal of the American Medical Association. Then answer the following
questions:
1. Does the body of the article imply a cause-and-effect relationship between
marital status and longevity in men? If so, quote specific lines where the
writer asserts this to be the case.
2. Does the headline imply a cause-and-effect relationship between marital
status and longevity in men? If so, how do you explain this headline choice
by the Web page editors? How would you reword the headline so that it is
factually correct?
3. Explain, using some of the terminology we have learned, why no
cause-and-effect relationship between marital status and longevity can be
asserted. Write a good-quality paragraph that you would not be ashamed to
read aloud.
4. Then write up #5.78 on p. 303. Keep careful records of your 20 trials
(record 2 numbers for each, as well as the results). We will combine
everyone’s results in class.
|
|
|
F 11/17/06
|
HW due: Read pp. 310-317; write #6.8 on p. 317.
|
|
|
M 11/20/06
|
HW due: Read pp. 317-322; write #6.9, 6.12. Warning: Not all of the answers in the
back of the book for #6.9 are correct.
|
|
|
T 11/21/06
|
HW due: Read the Monty
Hall problem and the Chest of Drawers
problems. Carefully prepare an answer for all the questions posed. You
must be prepared to justify your answers. Off-the-cuff answers, or answers
based on what you “feel” might be true, are not sufficient. If you base your
argument on an enumeration of the sample space, you must be prepared to prove
that the cases are equally likely. Wrong answers will receive no credit.
Answers that are not justified will receive no credit.
For example, the following answer is unacceptable for the Monty Hall problem:
“The probability that my original door is the winning door is 0.5, since
there are only two possibilities. Either my door has the prize, or the other
remaining door has the prize. Because this is clearly a 50/50 proposition,
with sample space {my door, the other door}, the answer is 0.5.” (This answer
is unacceptable because no proof is furnished that the two elements of the
sample space are equally likely. In fact, it is easy to show with a Monte
Carlo simulation that they are not equally likely. Perhaps the Monte Carlo
method is something you should consider.)
|
|
|
Break
|
Happy Thanksgiving. If you have a chance, please say
a prayer for my mother-in-law, Judith Mosier, who suffered a severe stroke
Nov. 19. Emergency surgery on Nov. 20 saved her life, but we do not yet know
if she is going to recover.
|
|
|
M 11/27/06
|
No additional written HW due. Please enjoy your
Thanksgiving break, and if you have any spare time, please use it to finish
up any previously assigned problems that you could not finish on the first
try.
|
|
|
T 11/28/06
|
HW due: First, please make the following two corrections to
your class notes.
1. Roosevelt defeated Landon in 1936,
not 1932 as I incorrectly stated in class. Check out this interesting source.
2. The actual percentage of Medicare expenses represented by care in the
final year of life is more than 25% (click here
for a legitimate source) but not as high as the 80% or 90%
figure one sometimes hears. My suspicion is that those speakers may be
engaging in Marilyn-speak (i.e., saying things that were not fully checked).
Second, perform simulations or analyses (WARNING!
simulations preferred) for the Monty
Hall problem and the Chest of Drawers
problems. I will ask for your raw data or the results of your analyses.
Guesses will not be accepted. Most of the answers given yesterday were wrong.
If you cite data, be sure to have enough trials to have some confidence in
your results. For example, 3 successes in 6 trials is not going to give much
insight at all into the true answer.
Show your work clearly. If you perform a simulation, organize your results
neatly in a table, and describe your simulation procedure with words and/or
diagrams.
As we did yesterday, prepare answers in the following order:
1. (Monty Hall) What is the probability that your original door is the
winning door?
2. (Chest A) If the coin you selected is gold, what is the probability that
the other coin in the same drawer is also gold?
3. (Chest B) If the coin you selected is gold, what is the probability that
the other coin in the same drawer is also gold?
For example, if you have a simulation that reveals 16 successes in 50 trials,
you would report your answer as 16/50.
|
|
|
W 11/29/06
|
HW due: Learn about odds
(see below) and answer the questions that follow. Also patch up any missing
pieces in yesterday’s assignment, since it may well be collected or graded
more closely.
The odds against an event are
(informally) the ratio of the losing ways to the winning ways. More
accurately, the odds against the
occurrence of event A can be defined as 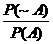 , where “P” means “probability of” and the tilde (~) means
negation. , where “P” means “probability of” and the tilde (~) means
negation.
Example: Compute the odds against
drawing an ace from the top of a well-shuffled deck.
Solution: Since the probability of
this event is 1/13, we have 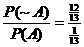 , or 12:1. , or 12:1.
Note that odds are not the same as probability. Laypeople and people who
don’t know any better will sometimes say things like, “The odds of winning
are 1 in 100.” If, in fact, the probability of winning is 0.01, then a
correct statement would be, “The odds in favor of winning are 1:99,” or
equivalently, “The odds against winning are 99:1.”
Also note that the odds, if computed according to our definition above, tell
you what the fair payoff would be if nobody was taking advantage of anybody.
Casinos, of course, will quote different odds, namely odds that ensure that
they make a profit.
Example: Compute the fair odds
against hitting red on the roulette wheel, and prove that these odds are
indeed fair.
Solution: In America, roulette
wheels have 38 numbers, 18 of which are red, 18 of which are black, and two
of which (0 and 00) guarantee the house edge. Therefore, the fair odds
against red are  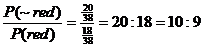 . .
To prove that these are indeed fair odds, we must compute the expected value of a typical bet (say,
$90). If we were paid off at fair odds, a $90 bet would pay $100 every time
we won (in addition to our $90, which we are allowed to keep), but every time
we lost, we would simply forfeit the $90.
To compute the expected value, we compute the probability-weighted average
payout. There is a probability of 20/38 of losing $90, and a probability of
18/38 of winning $100 net. A weighted average means that we multiply 20/38 by
(–90), we multiply 18/38 by (+100), and then we sum the two results. Answer:
$0. The odds are fair, because the expected value of the game is zero.
1. Compute the fair odds against hitting the number 13 on the roulette wheel.
2. Las Vegas casinos pay out at 35:1 if you bet on a roulette number and
manage to hit it. Why does this answer differ from your answer to #1?
3. Explain why Las Vegas casinos do not pay off red at 10:9 as computed in
the example above. What do you think the payoff odds for red are?
4. In Chest of Drawers B, what are the fair odds against the second coin’s
being gold, provided it is known that the first coin is gold?
5. In Chest of Drawers A, what odds would you offer a statistically challenged
person in order to both (a) encourage the person to take your bet and (b)
ensure that, in the long run, you make a handsome profit betting that the
second coin is gold if it is known that the first coin is gold?
6. Two people randomly choose a letter of the alphabet. What are the odds
against their choosing the same letter?
7. Thirty people, mutual strangers, are at a ballgame. What are the odds in
favor of the event that at least two of them have the same birthday (i.e.,
month and day)? Assume a uniform random distribution of birthdays, and ignore
leap years.
|
|
|
Th 11/30/06
|
No additional HW due. However, any previous HW
assignment may be collected. Mr. Andreoli will be your substitute teacher. He
will cover the following basics of analytic (“a priori”) probability:
Permutations and combinations
Events and their complements
Counting rules
General union rule
General intersection rule
Conditional probability formula
Independent events
Mutually exclusive events
Poker odds (time permitting)
|
|