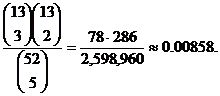|
|
General scoring rubric: There is 1 point possible per problem. To earn the
point, the student must have both correct numbers and correct labels. For
example, in #1, saying that 1/13 ¹ 0 does not earn any credit unless the student has
labeled the 1/13 as representing P(ace)
and has labeled the 0 as representing P(ace
| face).
Deduct half a point if the numbers and labels are essentially correct but
have some notational problems. For example, in #1, saying P(ace · face) = 3/169 is flat
wrong as it stands, since P(ace Ç face) = 0, but the student probably meant to say P(ace) · P(face) = 3/169. If the proof is correct other than for a
notational error of this type, mark the error and score the problem at half
credit.
|
|
|
|
|
1.
|
Prove that “ace” and “face
card” are not independent events.
Full credit: P(ace) = 1/13 ¹ P(ace |
face) = 0.
Also full credit: P(face) = 3/13 ¹ P(face |
ace) = 0.
Also full credit: P(face Ç ace) = 0 ¹ P(ace) · P(face) = (1/13) (3/13) = 3/169.
Showing both the product (1/13) (3/13) and the simplified answer 3/169 is not
required, but the student should show one or the other.
Half credit: Any of the above, but
with one or more notational errors.
No credit: A mere statement that
an ace is not a face card, or a statement that “ace” and “face” are mutually
exclusive, or a statement that P(face
Ç ace) = 0 without
further explanation. While true, these statements suggest that the student
does not fully understand the distinction between mutually exclusive and
independent events.
No credit: A statement to the effect that aces and face cards overlap and therefore
cannot be independent. This is false for two reasons: (1) aces and face cards
do not overlap, and (2) even if
they did, that is irrelevant to the proof of non-independence. It appears
that the student did not read the S6 solution, which explains that face cards
are jack, queen, and king, and it also appears that the student is murky on
the distinction between mutually exclusive and independent events.
No credit: Statements similar to
those in the proofs above (e.g., 1/13 ¹ 0) but without the probability labels.
|
|
|
|
|
2.
|
Compute the number of
bridge hands possible (13 cards selected as an SRS from a 52-card deck).
Full credit: 52C13 = 635,013,559,600.
Also full credit: Student uses 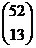 notation instead of 52C13. notation instead of 52C13.
Also full credit: Student writes
6.350 · 1011 or 6.35 · 1011 instead of 635,013,559,600.
Half credit: Student messes up the
scientific notation or writes  . (The fraction bar is not supposed to be included in the
“choose” notation.) . (The fraction bar is not supposed to be included in the
“choose” notation.)
No credit: Student gives a numeric
answer without including a “choose” notation label.
|
|
|
|
|
3.
|
Compute the probability of
obtaining 3 hearts and 2 clubs in a randomly dealt 5-card poker hand. (There
are 13 hearts and 13 clubs in a standard deck.)
Full credit: 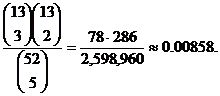
Also full credit: Equivalent work
(intermediate step optional) supporting an answer
close to 0.009.
Half credit: Notational error(s).
Half credit: Student demonstrates
correct use of multiplication rule (including work) to obtain correct
numerator, but student forgets to divide by 52C5 or divides by something else.
Half credit: Student knows that
the denominator is 52C5
(and actually writes both 52C5
and 2,598,960), but numerator does not have the two “choose” factors shown.
No credit: Answer for numerator,
denominator, or both, but without supporting “choose” labels.
No credit: Student shows that
denominator is 52C5
but does not compute the numeric value for the denominator. Numerator is
incorrect.
|
|
|
|
|
4.
|
Prove that “2” and “even
number” are not independent events when rolling a 6-sided fair die, numbered
1 through 6.
Full credit: P(two) = 1/6 ¹ P(two |
even) = 1/3.
Also full credit: P(even) = 1/2 ¹ P(even |
two) = 1.
Also full credit: P(two Ç even) = 1 ¹ P(two) · P(even) = (1/6) (1/2).
Simplification of (1/6) (1/2) as 1/12 is optional. (Do not add or deduct if
that is the only issue.)
Half credit: Any of the above, but
with one or more notational errors.
No credit: A mere statement that 2
is an even number, or a statement that “two” and “even” are not mutually
exclusive, or a statement that P(two
Ç even) ¹ 0 without further explanation. While true, these
statements suggest that the student does not fully understand the distinction
between mutually exclusive and independent events.
No credit: A statement to the
effect that “two” and “even” overlap and therefore cannot be independent.
This is irrelevant to the proof of non-independence. It appears that the
student is murky on the distinction between mutually exclusive and
independent events.
No credit: Statements such as P(two Ç even) = 0, or “events are mutually exclusive,” or
“events do not overlap.” These statements are doubly incorrect: They are not
only false but also irrelevant to the proof of non-independence.
No credit: Statements similar to
those in the proofs above (e.g., 1/6 ¹ 1/3) but without the probability labels.
|
|
|
|
|
5.
|
Two fair dice are rolled.
Compute the probability of obtaining “boxcars” (double 6).
Full credit: (1/6) (1/6) = 1/36.
Also full credit: P(double 6) = P(6) · P(6) = 1/36.
Half credit: P(6 · 6) = 1/36. (This is a
notational error.)
No credit: P(double 6) = 1/36. (There is
no work or explanation provided.)
Add 1 bonus point if student
writes that the (1/6) (1/6) multiplication is valid because the rolls are
independent.
|
|
|
|
|
6.
|
Two fair dice are rolled
twice. Compute the probability of obtaining “boxcars” on at least one of the
rolls.
Full credit: P(at least one double 6) = 1 – P(no double 6) = 1 – (35/36)2
» 0.055.
Half credit: Student obtains
correct answer but does not fully explain what is being subtracted from 1.
Half credit: Student proceeds as
above but makes one error: bungling the 35/36, raising 35/36 to a power other
than 2, or not calculating the final answer.
No credit: More than one error of
the type described above.
No credit: Answer of 1/36, 2/36,
1/18, 34/36, 17/18, or their decimal equivalents, regardless of any
accompanying explanation or work.
Add 1 bonus point if student
writes that the (35/36) (35/36) multiplication is valid because the rolls are
independent, but not if the student already has a bonus point from problem
#5.
|
|
|
|
|
7.
|
Two fair dice are rolled.
Compute the probability of obtaining a sum of 8.
Full credit: P(2, 6) + P(3, 5) + P(4, 4) + P(5, 3) + P(6, 2) = 1/36 + 1/36 + 1/36 + 1/36 + 1/36 = 5/36. (The
ordered pair notation is meant to suggest an ordered outcome. Imagine coloring
the dice as one red and one green and always calling the red die first. For
example, (2, 6) means 2 on the red die and 6 on the green die, and the
probability of such an outcome is 1/36 by problem #5 above.)
Also full credit: 5/36, justified
by a listing of the 5 possible equally likely ways this outcome could occur.
Half credit: Some answer other
than 5/36 but with a somewhat believable counting argument. For example, the
student may have forgotten that (2, 6) and (6, 2) are separate possibilities
and need to be counted twice.
Half credit: Answer of 5/36
without enumeration of cases.
No credit: Wrong answer
unaccompanied by useful enumeration of cases.
Add 1 bonus point if student
writes that addition of probabilities is justified because the cases are
mutually exclusive.
|
|
|
|
|
8.
|
Two fair dice are rolled.
Both of them fall on the linoleum floor where you cannot see them. A trusted
friend says, “At least one of the dice is a 6.” (Now, clearly this does not
always happen. Sometimes there will be no 6’s. However, we are considering a conditional probability situation
where at least one 6 is visible to your trusted friend, who always tells the
truth.)
Given that at least one of the dice is a 6, what is the probability that you
have rolled “boxcars”?
Full credit:
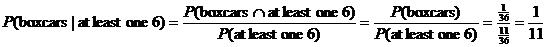
Also full credit: Enumeration of
the 11 equally likely ways that at least one 6 can be obtained, followed by
an observation that only 1 of these gives boxcars. The 11 ways are (1, 6),
(2, 6), (3, 6), (4, 6), (5, 6), (6, 6), (6, 1), (6, 2), (6, 3), (6, 4), and
(6, 5). Answer: 1/11.
Half credit: Conditional
probability formula leading to correct answer but with notational error(s).
Half credit: Reasonable but
unsuccessful attempt to use the conditional probability formula, provided
that the notation is completely correct, and provided that the final answer
is not 1/6.
No credit: Any answer that omits
recognition of conditional probability.
No credit: Any wrong answer that
uses the conditional probability formula but contains notational errors.
No credit: Answer of 1/6,
regardless of any accompanying work or explanation.
|
|
|
|
|
9, 10.
|
Add 2 points
if student’s estimate of score was within ±2 points of the true score on problems 1 through 8
(not counting bonus). However, if the paper is blank and the student estimate
is 0, add only 1 point.
|