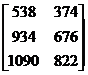|
#10.41
(1-sample t test)
|
(a) t = –2.1995 (Note: Book was expecting z = –2.1995, but the t test is more appropriate here.)
(b) P = .030168 with df = 99 (more correct than textbook answer of P = .0278 for z test)
Therefore, significant at the 5%
level. There is sufficient evidence that the true mean
m differs from .5.
(c) No, not significant at the 1% level. There is no evidence (at this
level, that is) that the
true mean m differs from .5.
|
|
|
|
|
#10.59
(1-sample t or z test)
|
(a) P = .382
(b) P = .1715
(c) P = .00135
|
|
|
|
|
#10.60
(1-sample t
or z C.I.)
|
(a) We are 99% confident that
the true mean SATM score is between 451.7 and 504.3.
(b) We are 99% confident that the true mean SATM score is between 469.8 and
486.2.
(c) We are 99% confident that the true mean SATM score is between 475.4 and
480.6.
|
|
|
|
|
#10.62
(binom.)
|
(a) No, since by chance
alone the expected number of such detections would be (by a
binomial distribution) np = 500(.01) =
5. The probability (assuming chance alone)
of seeing 4 or more detections is .736,
hardly a surprising outcome.
(b) Treat the initial study as a pilot study or a screening study, i.e., a
preliminary check
to see if there are any potential
psychics worthy of further testing. Then, design
and run fresh experiments on these 4
people to see if they seem to have any
psychic abilities. The original tests do not provide any evidence of psychic
ability,
since the data were not gathered in a
setting where the hypothesis was made in
advance.
|
|
|
|
|
#10.63
|
None of the above. The least
incorrect answer is (b), but it should be reworded as follows: “Is the
observed effect plausibly explained by chance alone?”
|
|
|
|
|
#10.64
|
No, all we can say is that
the difference in sample proportions is too large to be plausibly explained
by chance alone. With such a large sample (n1 + n2
= 5000), almost any difference will be statistically significant, but that is
not the same as saying that there is a strong preference (i.e., a large
difference between the sample proportions).
|
|
|
|
|
#10.65
(binom.)
|
(a) The question is
ambiguously worded. If the question is supposed to be
P(exactly one test of the 77 is significant at a = .05), then the answer is .078.
If the question is supposed to be
P(at least one test of the 77 is significant at a = .05), then the answer is .981.
The most likely interpretation, however, is
“For a single test, specified in advance,
what is P(significant
at a = .05)?” The
answer is .05 by the definition of a. On the AP exam, questions are worded better.
(b) By a binomial distribution, P(2 or more tests of 77 are significant at a = .05) = .903.
This is hardly a surprising outcome. It
would be much more surprising if we did
not
see at least 2 significant tests out of 77. The expected number, assuming
chance
alone, is np = 77(.05) = 3.85, or nearly
4.
|
|
|
|
|
#10.68
(normal distrib., def. of Type I and Type II error)
|
Note:
Throughout this problem, the sampling distribution has s.e.
= 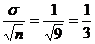 . We . We
will use this value of 1/3 in all of the “normalcdf”
computations that are required below.
(a) P(Type
I error) = P(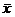 > 0 | H0
true) = P( > 0 | H0
true) = P(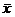 > 0 | m = 0) = .5 by inspection. > 0 | m = 0) = .5 by inspection.
Reason: The sampling distribution of 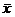 is normal and, if H0 is true, centered is normal and, if H0 is true, centered
on 0. Note:
It is technically incorrect to say that 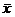 follows a t distribution follows a t distribution
with df = 8,
since it is given that the underlying data distribution is normal.
(b) P(Type
II error for m = .3 alternative) = P(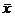 < 0 | m = .3) = .184 < 0 | m = .3) = .184
(c) P(Type II error for m = 1 alternative) = P(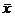 < 0 | m = 1) = .00135 < 0 | m = 1) = .00135
This is a rather strange problem, since the REJECT/DO NOT REJECT boundary is
placed at a most unusual location, namely at the 0 mark. In a more realistic
problem, the boundary would be pegged to a typical a level of, say, .05. If we were to modify the
problem in that way, then we must first convert the cutoff value from a z* value of 1.645 (from the table) to a
numeric value of .548. Here are the steps:
z = (obs. – exp.)/s.e.
1.645 = (obs. – 0)/(1/3)
.548 = obs.
(amod)
P(Type I
error) = P(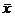 > .548 | m = 0) = .05. We can also get the answer of .05 without
any work by remembering that the probability of Type I error always equals
the a level of the test. > .548 | m = 0) = .05. We can also get the answer of .05 without
any work by remembering that the probability of Type I error always equals
the a level of the test.
(bmod)
P(Type II error) = P(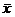 < .548 | m = .3) = .772 < .548 | m = .3) = .772
(cmod)
P(Type II error) = P(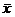 < .548 | m = 1) = .088 < .548 | m = 1) = .088
|
|
|
|
|
#11.22
(1-sample t C.I.)
|
(a) We are 95% confident
that the true mean number of mixers is between 21.5 and 26.5.
(b) The sample size is large enough to make the sampling distribution of 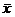 approximately approximately
normal. [See box on p. 616.]
|
|
|
|
|
#11.43 (2-sample t
test and 2-sample t C.I.)
|
(a) Let m1 = true
mean angular knee velocity of skilled rowers, m2 = true
" " " " of novices.
H0:
m1 = m2
Ha:
m1 > m2
(b) P = .0104/2 = .0052 Ž There is strong evidence (n1 = 10, n2
= 8, t = 3.1583, P = .0052)
that the true mean angular knee velocity
is greater for skilled rowers than for novices.
(c) We are 90% confident that the true mean angular knee velocity for skilled
rowers is
between .498 and 1.848 units greater than
for novices.
Alternate wording: We are 90% confident
that the true mean difference between
angular knee velocities for skilled
versus unskilled rowers is between .498 and
1.848 units.
Alternate wording: We are 90% confident
that the true mean difference of angular
knee velocities for skilled versus
unskilled rowers is 1.173 ± .675 units.
|
|
|
|
|
#12.8
(1-prop. z C.I. and 1-prop. z test)
|
(a) We are 95% confident
that the true proportion of first-year students at this university
who feel this way is between .594 and
.726.
(b) Let p = true proportion at the
university who feel this way.
H0:
p = .73
Ha:
p ¹ .73
z
= –2.2298
P
= .025759
There is good evidence (n = 200, 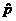 = .66, z = –2.23,
P = .0258) that the true = .66, z = –2.23,
P = .0258) that the true
proportion of students at this university
who feel this way differs from .73.
(c) SRS ü
N
³ 10n (reasonable if this is a large university with 2000 or more
students) ü
# of successes = np » 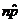 = 200(.66) = 132 ³ 10 ü = 200(.66) = 132 ³ 10 ü
# of failures = nq » 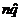 = 200(.34) = 68 ³ 10 ü = 200(.34) = 68 ³ 10 ü
|
|
|
|
|
#12.39
(mixture of 1-prop. and 2-prop. z
tests)
|
(a)
No, since the 2-sided P-value
(1-prop. z test) is .1849.
(b) Yes, since the 1-sided P-value (2-prop. z
test) is .0255.
(c) For (a) we have
SRS ü
N
large enough (given wording: “... large pop. of athletes
the univ. will admit ...”) ü
# of successes = 45 ³ 10 ü
# of failures = 29 ³ 10 ü
For (b) we have
2 indep. SRS’s ü (no dependence between males and females) ü
N1
and N2 both sufficiently
large (see wording cited above) ü
# of female successes = 21 ³ 5 ü
# of female failures = 7 ³ 5 ü
# of male successes = 24 ³ 5 ü
# of male failures = 22 ³ 5 ü
For baseball players, a sample of 5 is too small to allow
at least 5 successes and 5 failures.
|
|
|
|
|
#12.40
(trick question, 2-sample t test)
|
(a) These are not
proportions of success. The percentages are simply averages (i.e., means)
of investment performance. These
statistics could just as well have been stated as
“pennies of revenue per dollar in highly
regulated businesses,” which would
eliminate the % sign altogether.
(b) 2-sample t (What additional
data would you need in order to carry out the test?)
|
|
|
|
|
#13.27a
(2-way c2 test for homo-geneity of
props.)
|
Not significant, because
the P-value is .591.
Note: This problem is tricky.
Remember that your matrix entries for a 2-way c2 test
are counts and that they must
represent either an SRS, several independent SRS’s, or an entire population cut along 2 categorical
variables. The situation we have here is 3 independent SRS’s,
but we have to be careful to include both the “anti-Clinton” tallies (column
1) and “pro-Clinton” tallies (column 2). Therefore, the matrix we use is as
follows:
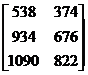
|
|
|
|
|
#13.28
(c2 g.o.f.)
|
Marginal percentages for
population were given: 15.3%, 22.0%, 24.8%, 19.8%, 18.1%.
Marginal percentages for sample: 31.2%, 29.5%, 18.9%, 14.8%, 5.6%.
The P-value of 3.48 · 10–34
(i.e., essentially 0) shows that the score distribution of the sample differs
significantly from the score distribution in the overall population of 7600
test-takers.
|
|
|
|
|
#14.18c
(LSRL t test)
|
H0: b = 0
Ha:
b > 0
Or, if you prefer:
H0:
r = 0
Ha:
r > 0
t
= 4.28, df = 15, P = .0005 (one-tailed, hence half the P value shown in printout)
|