Monthly Schedule

(MODD, Period F)

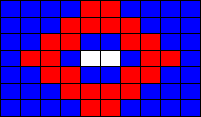
W 11/1/06	HW due (suggested): Develop a protocol that captures all the information of our original bitmap in fewer than 16 bytes. Here is our 16-byte bitmap file: 0800 0C00 89CD A2AA 289C F3C4 9249 2F3C Your protocol is what you should write. In other words, explain precisely how the data will give instructions for flipping pixels on and off. If you do a good job of this, anyone in the class should be able to encode or decode the bitmap using your protocol.
Th 11/2/06	HW due: Either redo yesterday’s assignment, or implement my protocol below in order to decode the given bitmap. (Draw a grid, or use graph paper. Follow the protocol instructions in order to see the secret picture.) Bitmap data in hex: 07 00 38 00 00 03 3C 00 00 00 00 78 C1 1A 18 79 E1 EF 81 20 31 24 81 01 28 99 20 61 24 99 E1 2F 89 20 C1 24 88 21 29 70 C1 82 18 71 E1 EF 00 03 FC 00 00 00 00 1A Protocol: 1. The first 2 bytes indicate the vertical number of pixels (stored little-endian). 2. The next 2 bytes indicate the horizontal number of pixels (stored little-endian). 3. Each of the remaining nybbles (i.e., hex digits) is to be interpreted as a pattern of blacks and whites, where 1=black, 0=white. For example, the hex digit B is equivalent to binary 1011, therefore representing black, white, black, black. Another example would be hex digit 5, which would be binary 0101, hence white, black, white, black. 4. Work left to right until the first row is filled in. Then fill in the additional rows, working left to right in each case. 5. The Ctrl+Z character (byte value 26 decimal) indicates end of file. After HW check: “Fun Friday on Thursday.”
F 11/3/06	No school.
M 11/6/06	HW due: 1. Using graph paper or a homemade grid similar to my board sketches, create a 12 x 36 bitmapped image. That means 12 rows, 36 columns. Choose a pattern, design, or secret message that would be difficult for someone to guess. You may use black-and-white (one bit per pixel), or if you wish, you may use multiple colors, in which case you would need enough bits per pixel to indicate the proper choice of color from some palette that you would need to define. Put your name on your paper, and bring it to class so that it can be used as a grading key. If you are having trouble doing this, please see the monochrome bitmap example or the more complicated 4-color bitmap example. 2. Create (a) a compression protocol (i.e., a set of rules that describe how bytes are to be interpreted) and (b) the actual byte sequence in hex that would allow a receiver to reconstruct your image file. Put 2(a) and 2(b) on the same sheet of paper, but use a different sheet of paper from #1. Write legibly, since other students will be attempting to use your protocol to decode your secret bitmap. Note 1: You cannot use the protocol that I published in the 11/2/2006 calendar entry, because that is not a compression protocol. That is a protocol for uncompressed data. Try to dream up something along the lines of the tokenizing, run-length encoding, or multibit clustering protocols that we discussed in class. Use your imagination, and try to be clever if you can. Warning: Whatever you come up with must be clearly described in your protocol, because otherwise the rest of us will have trouble decoding your file. Note 2: The 11/2/2006 protocol applied to a monochrome 12 x 36 bitmap would require 59 bytes (12 x 36 = 432 bits = 54 bytes, and we added a 4-byte header for dimension information and a 1-byte indicator for end of file). However, do not worry if your answer to #2(b) turns out to be longer than 59 bytes. It is often the case that the benefit of compression is not seen in small files because the “overhead” of the compression scheme takes up too large a percentage of the total. Clearly, though, a large bitmapped image having many neighboring pixels all the same color, or many repeated patterns, would benefit greatly from a compression protocol. Please try doing this on your own, but if you are stuck and need some hints, you may look at the monochrome run-length protocol example or the 4-color run-length protocol example. Both of these examples use run-length encoding, but not in a very clever way.
T 11/7/06	HW due: First, several people need to finish yesterday’s assignment. Remember, you need a byte stream and a written protocol for credit. The illustration is fun, but it is probably the least important part of the assignment. Second, read the following student protocol and byte stream. Try to find at least 3 errors. How would you recommend modifying this without redoing it completely? (In other words, correct the errors in the protocol and/or byte stream.) Protocol First digit: if it is a 1, first set of pixels are black; if it is a 0, first set are white. From then on, each new digit is the number of pixels, with the color reversing each time. Each row ends with an F in order to help us keep track of where we are. The dimensions of 12 rows and 36 pixels per row are assumed to be known in advance. E.g., 1, 5, A, 3, 12, F Because the first digit is one, the boxes start out being black. Five black boxes, then A (10) white, then 3 black, then 18 (hex 12) white. Total of 36 boxes, and the first row is finished. Hex digits 0, 24, F 0, 1, 1, 5, 1, 2, 3, 2, 5, 3, 5, 8, F 0, 1, 2, 3, 2, 1, 1, 3, 1, 2, 1, 3, 1, 3, 1, 3, 1, 7, F 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 1, 2, 1, 4, 1, 2, 1, 4, 1, 6, F 0, 1, 1, 2, 1, 2, 1, 1, 1, 3, 1, 2, 1, 3, 1, 3, 1, 3, 1, 7, F 0, 1, 1, 5, 1, 2, 3, 2, 5, 3, 5, 8, F 0, 24, F 0, B, 1, 2, 3, 3, 3, D, F 0, 1, 3, 1, 1, 2, 1, 2, 1, 2, 1, 1, 1, 2, 1, 10, F 0, 1, 1, 3, 1, 2, 1, 2, 1, 2, 3, 2, 3, E, F 0, 1, 1, 3, 1, 2, 1, 2, 1, 2, 1, 7, 1, D, F 0, 1, 1, 4, 3, 2, 1, 2, 3, 2, 4, D, F
W 11/8/06	HW due: Read Chapter 6 (goal of at least pp. 297-312 for today). Since we will cover this entire chapter, you may read ahead if you wish.
Th 11/9/06	HW due: Write p. 312 #1, 2, 3, 4, 5, 7.
F 11/10/06	Guest Nanotechnology Speaker: Dr. David Nagel, George Washington University. Whatever you do, do not miss this class!
M 11/13/06	HW due: Read pp. 313-323. In class: You will teach Mr. Kelley the high points from last Friday’s briefing, and then you will work on the MODD Nanostravaganza puzzle (printed version). A Web-based interactive version is also available. You will probably need Mr. Kelley’s help for 63 Across, 4 Down, and 18 Down.
T 11/14/06	HW due: Write p. 324 #1-9 all. Also, if you did not turn in the puzzle yesterday, then finish it up and turn it in today. You may turn in either the printed version or a screen print of the interactive version.
W 11/15/06	HW due: Read pp. 324-330, especially the example on p. 330. Also, everyone except Chris needs to finish the crossword puzzle. You may use Web resources, parents, and friends (even classmates, if you split the workload fairly). The only thing that is not permitted is copying answers from someone who already knows them. In other words, if you are working together, you should be doing your fair share of the work, not freeloading.
Th 11/16/06	No additional HW due. Think about or begin working on your semester project.
F 11/17/06	HW due: Read pp. 331-334; write p. 331 #1-5 all.
M 11/20/06	HW due: Work on your semester project. (This could consist of performing some initial research, checking out some books at the library, reading some articles, etc.) Although there is no additional written work due today, it is possible that some previously assigned problems will be collected and graded. For problems that have been gone over in class, you are expected to have correct solutions by now.
T 11/21/06	HW due: Prepare a list of 8 or 9 review questions to help you prepare for your upcoming test on compression and error correction. (Gödel’s Incompleteness Theorem, Russell’s paradox, and the concept of a Turing machine will also be included.) You may use questions from the book, or you may adapt some questions from last year’s test (nearly all of which are fair game again this year). Hints: bps means bits per second, and baud means symbols per second. If each symbol is a bit, then baud rate and bit rate are the same, but if each symbol is a hex digit (i.e., one of 16 possible tones or modulation patterns that could be sent), then the bit rate is 4 times the baud rate, since each symbol represents 4 bits. Pick problems that test not only knowledge of concepts but also the ability to think and to apply those concepts. Your score will be based on the quality of the questions you come up with. Bonus points for (1) putting your questions on index cards, one question per card, and (2) writing some original questions, not lifting all of them from me or from the textbook. Not all of your questions need to be original, but you should try to write at least a few of them yourself. A good way to learn is to imagine that you are a teacher testing someone on the most important material.
Break	Happy Thanksgiving. If you have a chance, please say a prayer for my mother-in-law, Judith Mosier, who suffered a severe stroke Nov. 19. Emergency surgery on Nov. 20 saved her life, but we do not yet know if she is going to recover.
M 11/27/06	No additional written HW due. Please enjoy your Thanksgiving break, and if you have any spare time, please use it to finish up any previously assigned problems that you could not finish on the first try, especially your test study questions. In class: Review.
T 11/28/06	Test. Please see the 11/21 calendar entry for list of topics and some sample questions. Additional questions will be drawn from the assigned HW and class discussion.
W 11/29/06	In class today: Multiple-Choice Test Segment. Also, hand in your protocols from yesterday. (The problem is repeated below for your convenience.) Be sure to see Andrew if you have any uncertainty about how to engineer a color map in your protocol. Protocol Problem: At least one field must be stored little-endian (be sure to mention this in your protocol). Give protocol including description of dimension header, color map format, format for body of file, and all instructions for decoding. Give byte contents in hex. Remember, in your protocol, you do not define colors; you define color codes. That is, you state how the color codes will be defined in the file. Hint: red = FF0000h, blue = 0000FFh, and white = FFFFFFh. You may wish also to define a color code for black = 000000h, even though a fourth color is not used in the specimen file. Specimen:
Th 11/30/06	Come to class for attendance to be taken. Also hand in your protocol problem if you have not already done so. The remainder of the period will be for working on your semester project.

---

Return to the MODD Zone

Return to Mr. Hansen’s home page

Return to Mathematics Department home page

Return to St. Albans home page

Last updated: 04 Dec 2006