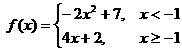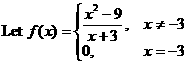IntroCal / Mr. Hansen

Name: _______________________________________

9/20/2006

Mr. Hansen’s use only (bonus point for spare batteries): _______

 

Test on §§1.1 through 1.3 and Class Discussion

Please read:

 

1.
(9)

What is meant by a “formal system”? Write a short explanation (5-10 words should suffice):

_______________________________________________________________
What word beginning with the letter C do we use to refer to a formal system? __________
When we put the word “the” in front of that word starting with C, we have a subject whose
three principal topics are
       (1) _________________________ (i.e., instantaneous rates of change),
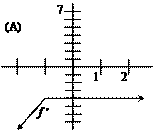
       (2) antiderivatives (a.k.a. _________________________ integrals), and
       (3) definite integrals (i.e., accumulations of rates of change).

 

 

2.
(8)

 

 

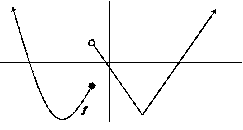
For the function f whose graph is shown above, sketch a believable f ¢ function on the same set of axes. Make sure that anything that needs to line up vertically actually does.

 

 

3.
(10)

 

Years after 1900

U.S. Debt ($billions)

 

 

 

 

 

 

 

20

25.9

 

 

 

 

 

 

 

30

16.2

 

 

 

 

 

 

 

40

43.0

 

 

 

 

 

 

 

50

257.4

 

 

 

 

 

 

 

60

290.2

 

 

 

 

 

 

 

70

389.2

 

 

 

 

 

 

 

80

930.2

 

 

 

 

 

 

 

90

3,233.3

 

 

 

 

 

 

 

 

For the data set above, compute an exponential regression fit and a linear regression fit.
Exponential fit equation: y » _______________________________
Linear fit equation: y » _______________________________

 

 

 

Use your function equations to estimate the U.S. federal debt at the end of Fiscal Year 2005 (i.e., 105 years after 1900). Do not punch 2005 into your calculator. If you do, you will get nonsense.

 

 

 

Exponential estimate of 2005 debt » _______________________________

 

Linear estimate of 2005 debt » _______________________________

 

 

4.
(6)

Even if you could not answer #3, you can answer the following questions.
Which model (exponential or linear) does a better job of predicting the 2005 U.S. federal debt of $7.933 trillion? __________________

In the exponential model, the annual growth rate is approximately 7.5%. Estimate the number of years that this model predicts for the debt to double. Use either a “Precal” method or the shortcut that we learned in class. Show your work.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5.
(5)

Consider the points A(–3, 4) and B(–1, –6). Compute Dx, Dy, the slope m, and an equation (any form OK) of line AB.

 

Dx = _____

Dy = _____

m = _____

Equation of line: ________________________

 

 

 

 

 

 

 

 

 

 

 

 

6.

Which of the following is an example of a calculus?

 

(A) balancing equations in chemistry
(B) writing a speech for public speaking class
(C) painting a watercolor

(D) composing a song
(E) designing a health-related experiment

 

 

7.

The word “calculation” is derived from a Latin word meaning . . .

 

(A) clay pot
(B) stone tablet
(C) pebble

(D) vessel
(E) money

 

 

8.

The notation f ¢(x) means the derivative function evaluated at x. If f (x) = |x|, then f ¢(0) is . . .

 

(A) 0
(B) 1
(C) –1

(D) ±1
(E) undefined

 

 

9.

If f (x) = x2 and g(x) = sin x + 3, then f (g(p)) equals . . .

 

(A) sin 9 + 3
(B) sin 12
(C) sin 81 + 3

(D) 9
(E) undefined

 

 

10.

The rule of GNAV means that we should be willing to tackle problems . . .

 

(A) graphically, numerically, algebraically (or analytically), and/or visually
(B) generally, non-intuitively, algebraically (or analytically), and/or visually
(C) graphically, non-intuitively, algebraically (or analytically), and/or visually
(D) graphically, non-intuitively, algebraically (or analytically), and/or verbally
(E) graphically, numerically, algebraically (or analytically), and/or verbally

 

 

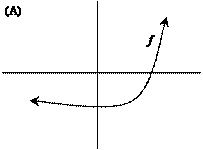
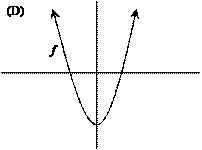
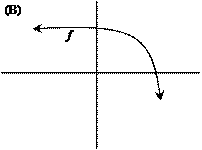
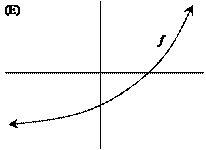
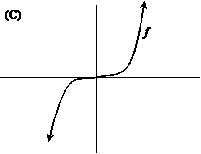
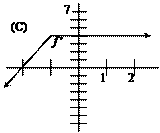
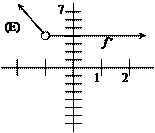
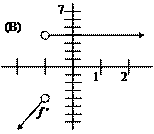
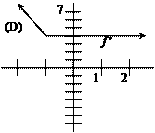
11.

The notation f ¢¢ means the derivative of f ¢ (i.e., the second derivative of f itself). For which function f below are both f ¢ and f ¢¢ always positive?

 

 

 

 

 

 

 

 

 

 

 

 

12.

Let a function be defined piecewise as
Which graph correctly illustrates f ¢?

 

 

 

 

 

 

 

 

13.






For this function, f (–3) is . . .

 

(A) 0
(B) –3
(C) –6

(D) –9
(E) undefined

 

 

14.

For the function f defined in #13, and for x ¹ –3, f (x) is . . .

 

(A) x
(B) x – 3
(C) x – 6

(D) x – 9
(E) undefined

 

 

15.

For the function f defined in #13, and for x ¹ –3, f ¢(x) is . . .

 

(A) 0
(B) 1
(C) –1

(D) –3
(E) undefined

 

 

16.

In #13, Df is . . .

 

(A) (–¥, –3] È [–3, ¥)
(B) (–¥, –3) È (–3, ¥)
(C) (–¥, –3] È (–3, ¥)

(D) (–¥, –3) È [–3, ¥)
(E) Â

 

 

17.

What useful rule of thumb did we learn?

 

(A) the Rule of 72 for exponential growth
(B) the Rule of 72 for power growth
(C) the Rule of 88 for exponential growth
(D) the Rule of 88 for power growth
(E) the Rule of 88 for tuning a piano with a geometric sequence

 

 

18.

To analyze something means . . .

 

(A) to combine many unrelated facts into a new whole
(B) to break the task down into smaller pieces
(C) to compute the numeric answer to a problem
(D) to solve the problem in question, even if it is not numeric
(E) to attempt to solve the problem in question, even if it is not numeric