|
T 5/1/07
|
Optional
HW due (bonus): Enter the program
below named EULER. The more people who enter this, the faster we can get
going in class. If you do not have time to enter it, we will pass it around
with a link cable. The program is fairly easy to understand, except for the
last 10 lines. Can you figure out exactly what the program is doing?
PROGRAM:EULER
:ClrHome
:Disp "PROGRAM: EULER"
:Output(3,1,"WRITTEN BY E.M.")
:Output(4,1,"HANSEN, ST.")
:Output(5,1,"ALBANS SCHOOL.")
:Output(6,1,"Y1 IS ASSUMED TO")
:Output(7,1,"CONTAIN DY/DX.")
:Output(8,1," ")
:0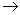 I I
:ClrList L1,L2
:Prompt X,Y,N,H
:Lbl A
:I+1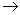 I I
:Y+HY1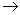 Y Y
:X+H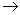 X X
:X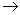 L1(I) L1(I)
:Y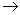 L2(I) L2(I)
:If I<N
:Then
:Goto A
:End
:Disp "CHECK L1,L2"
|
|
|
W 5/2/07
|
HW due:
1. Use BIGSLOPE to sketch the slope field for the diff. eq. dy/dx
= x2. Carefully
transcribe the results onto your HW paper. (Note: This slope field is also very easy to do by hand in case
you have lost your BIGSLOPE program.)
2. On your diagram, carefully sketch the particular solution that passes
through (3, 1).
3. Use pencil and paper to solve the initial value problem posed in #1 and
#2. Show your work. (We did this in class yesterday, except that we did not
show the work.) Manually punch the solution into Y2 (not Y1)
so that it can be graphed later.
4. Use EULER with initial condition (3, 1), 20 intervals, and a step size of
0.5 to estimate y(13). Remember
that before running EULER, you will need to enter the diff. eq. expression
for dy/dx (namely, x2)
into Y1. Write your answer for y(13)
correct to 3 decimal places.
5. Turn the display of Y1 off. Then press 2nd STATPLOT and modify
Plot1 so that it is set to display a scatterplot (first icon) with Xlist=L1
and Ylist=L2. Make sure that Plot1 is set to “On” and that Plot2
and Plot3 are set to “Off.” Press ZOOM 9 and transcribe the graph onto your
HW paper.
6. Complete the sentence: The Euler’s Method estimates for y seem to be slightly ______ the true
solution curve in most cases.
7. Compare your answer for #4 with Y2(13), which is the true value
of the solution when x = 13. Which
answer is larger, and by how much?
8. Rerun EULER with initial condition (3, 1), 40 intervals, and a step size
of 0.25. Write the new estimate for y(13).
By how much does this differ from the true value of the solution when x = 13?
9. Explain why the procedure in #8 gives a result that is closer to the true
value of y(13).
10. Explain why it is that no matter how small a value of h you enter when running EULER, the
estimate for y(13) will always be
somewhat on the low side.
11. It appears that Euler’s Method consistently underestimates the true
solution track over the interval [3, 13]. Are there diff. eqs. that would
cause Euler’s Method to overestimate
the solution? Explain briefly how this might be possible.
12. What feature of a function (first derivative, second derivative, etc.)
tells us how fast and in what direction the function is changing at any
particular value of x?
13. What feature of a function (first derivative, second derivative, etc.)
tells us how fast and in what direction the function is curving at any particular value of x?
14. Euler’s Method can be summarized as follows. Given an initial condition (x0, y0), use each previous point to generate the next
point in the list by means of the formulas
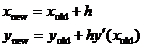
In which lines is the EULER program doing exactly this? (You may count
backwards from the end.)
15. How does Euler’s Method know how to evaluate the expression 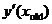 that was shown
above? that was shown
above?
16. Is it possible for a computer program to estimate 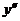 if the values for if the values for 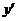 are known? are known?
17. How would you suggest doing #16? (A bit of vagueness is permitted.) Hint: Think of how we estimated
derivatives last fall.
18. Suggest a refinement to Euler’s Method that might improve its accuracy
without using a smaller step size.
|
|
|
Th 5/3/07
|
HW due:
1. Finish yesterday’s assignment if you have not already done so. We delayed the
scan in deference to the people who were affected by yesterday morning’s
webserver outage. Today’s assignment will be shorter so that you should be
able to do both in about 50 minutes.
2. Using the window [–5, 5] ´ [–3.5, 3.5], sketch the slope field for the diff. eq. 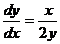 . .
3. Write the sentences and fill in the blanks:
“An initial condition located on the positive x-axis will have a solution that resembles the letter ______ . If
the initial condition is on the negative x-axis,
the solution would be a mirror image, like a _________ parenthesis. If the
initial condition is on the positive y-axis,
the solution would resemble the letter ______ , and if the initial condition
is on the negative y-axis, the
solution would look like a little bit like half of the famous logo for the
_____________ chain of hamburger restaurants.”
4. Given the initial condition (–1, 3), use Euler’s method to estimate y when x = 0.95 and when x =
1. (You can generate both answers in one pass by setting a step size of
0.05.)
5. Sometimes you may see “ridgelines” in a slope field, as we discussed in
class yesterday. The ridgelines for this slope field cross at the origin and
make a letter X. Find the equations of these ridgelines. (Show your work.)
Hint: These lines would have the
property that the result of taking an Euler Method step would give you a new
point (xnew, ynew) with unchanged slope.
In other words, plugging (xnew,
ynew) into the diff. eq.
should yield the same number for dy/dx that you would get by plugging (xold, yold) into the diff. eq.; by writing an equation and
plugging in you should eventually be able to get the equations of the
ridgelines.
Alternate hint: The previous hint
works fine, but if your algebra is weak and your calculus is strong, you may
find the following procedure easier. The ridgelines have the property that
for points along the ridgelines, the second derivative is 0. (Reason: The
ridgelines are lines.) See where
that leads you.
|
|
|
F 5/4/07
|
No class today (Tommy Walker film in Trapier
Theater).
|
|
|
M 5/7/07
|
HW due: The last two assignments (due 5/2 and 5/3) will be
collected or closely inspected. That means that you need to patch up your placeholders.
A giant “?” is not a placeholder. All that tells me is that you read the
hint, found it confusing, and gave up. Well, guess what. That is not going to
cut it in the work world. If there is nothing else that you learn from this
class, I want you to learn to be resourceful. At a minimum, you need to ask
me for help if you are stuck. (Better still would be to find some personal
reservoir of focus and bring it to bear on these problems.)
The questions are challenging, yes, but not impossible. Turn off your iPod,
set your papers down on a large work area, turn the lights up bright, kick
your younger siblings out of the room, and THINK.
Two additional questions for today:
1. Concoct a moderately difficult diff. eq. that contains a mixture of x’s and y’s, preferably one that produces an interesting-looking slope
field. Here is an example, though you can’t use this one:
dy/dx + 2y – y2 = xy – 3
Plot your slope field carefully and neatly on a suitable window. Show your
tick marks. Be sure to write down your diff. eq. as well.
2. Give a classmate your diff. eq. and tell him to guess an initial condition
at least 3 units away from the origin so that the solution will pass near the
origin. For example, (–2, 2) would qualify, but (1, 1.5) would not, since by
the distance formula, (1, 1.5) is only about 1.8 units away from the origin.
Then assign yourself a grade based on how well you stumped your classmate.
Record his guess on your HW paper, and then use Euler’s Method to generate a
sequence of points to see how close his solution comes to the origin at its
closest approach.
Note: Clearly, some diff. eqs. will
do a good job of stumping people, and some are ridiculously easy to solve.
For example, it is quite obvious (isn’t it?) by looking at the slope field
for dy/dx + x/10 + y = 0 that almost any initial
condition at all that has x < –3
will pass close to the origin. (Look at the slope field. It looks like a
giant funnel leading to the origin.) You’re going to have to be trickier than
that if you want to stump your friends.
Attendance
Rules for AP Weeks (May 7-11 and May 14-18)
Unless otherwise posted on this Web page, class will
be held each day at the normal time, and attendance will be taken. You are
automatically excused if you have a morning AP exam and if you actually
attend the exam. (If you fail to attend an exam for which you are scheduled,
you will be charged with a cut if you have any remaining, otherwise a point
penalty of 1 point per minute of class missed.)
Note: If you have an afternoon exam
and wish to be excused from IntroCal class, you must submit a written request
in advance (e-mail preferred). I will normally approve such requests, but
approval is not automatic. You must make the request yourself.
|
|
|
T 5/8/07
|
HW due: The three previous assignments (5/2, 5/3, and 5/7)
plus the following essay.
1. Write an essay (paragraph) of approximately 250 words discussing theme (a)
plus one or more of the others (your choice):
(a) (Required.) My personal effort over the weekend fell short of the mark
because ____________ .
(b) Courage is not the absence of fear. Courage, instead, consists of action
in the face of fear.
(c) Confronting one’s own shortcomings can be a scary action to take.
(d) Motivation follows action. It
usually does not precede action.
I have been teaching long enough to know that threats become less and less
effective as students approach graduation. I also know that I cannot motivate
you. Only you can motivate you. We are going to understand how to do better
in the future, so that 85% or more of the class will have good HW by Tuesday,
May 8.
Helpful hint: When looking at your
slope fields from the 5/3 assignment yesterday, I noticed that many students
seemed to have a ridgeline along the x-axis.
That is clearly impossible, since a ridgeline along the x-axis means a slope of 0. (That can’t happen if the diff. eq. is
dy/dx = x/(2y), since you would be dividing by 0
at any point along the x-axis.)
What I think happened is that about half of the class forgot the parentheses.
Please make that correction if necessary and re-do your slope field.
|
|
|
W 5/9/07
|
HW due: Copy the following corrected solution from the 5/3
assignment onto a fresh sheet of paper. Then answer the questions that
follow.
5. Since dy/dx = x/(2y), d2y/dx2 = (2y – 2xy ¢)/(2y)2 by QR.
To find solutions that are ridgelines, we set
the second derivative to 0 and solve for y.
(2y –
2xy ¢)/(2y)2
= 0
2y –
2xy ¢ = 0
2y =
2xy ¢
2y =
2x (x/(2y))
2y = x2/y
y2
= x2/2
y = ±x/Ö2
Answer: two lines crossing at the origin. One
has slope 1/Ö2, and the other has slope –1/Ö2.
6. On a clean version of the slope field (you may use the one you made in
class yesterday if you wish), carefully sketch the two ridgelines you found
in #5. Make sure that you get the slopes correct.
7. Provide a reason for each of the 7 algebraic steps in #5.
8. Rate the difficulty level of the original question #5. (Be honest.)
9. If Mr. Hansen teaches IntroCal again in 2007-08, should he include the
original version of #5 as a homework question? Explain your reasoning.
|
|
|
Th 5/10/07
|
HW due: If you have not already read the Lessons from the Pentagon handout,
please read through it so that you are up to speed. That shouldn’t take very
long, and reading notes are not required. Then, please make sure that you are
up to date on previously assigned written work. (Since there are multiple
recent homework assignments, a multiple scan is likely.)
In class: A group activity that I hope you will enjoy.
|
|
|
F 5/11/07
|
HW due:
1. The 5/9 assignment will be graded a second time. Today there will be two scores:
one score of 0-4 for neatness/completeness, and a second score of 0-4 for
accuracy. Make sure that all of your answers and reasons are correct. No
“nonsense characters” are permitted. For example, if your browser or printer
cannot correctly display the symbol for “prime” ( ¢ ) or “square root” ( Ö ), then you need to use your common sense to make
the adjustments on your own.
2. Answer the question posed at the end of #34 in the Lessons from the Pentagon handout.
This will count as 4 points. Write legibly.
3. Be prepared to hand in and/or make an oral presentation of your in-class open-ended questions. Where
applicable, cite one or more Lessons
from the Pentagon that apply to each question. (You may cite them by
number.) Complete sentences are not required, but legibility and coherence of
thought are required. No half-baked, mumbled, murky answers, please.
Warning: Some students have told me
(truthfully) that homework at this time of year, especially in the midst of
AP exams, is not their highest priority. OK, I can accept that. Please be
aware, though, that there is a consequence. At this writing, there are only
about 200 points possible in the fourth quarter. If you do the math, you
quickly realize that skipping a double scan (8 points) will lower your
quarter grade by about 4 points, or almost half a letter grade. Because we
did not have any tests this quarter, the difference between a low A and a
high F is only about 60 points. There is nobody failing as of last week (the
last time I ran averages), but the grade distribution is not exactly stellar:
A+: 1 student
A: 1 student
B+: 3 students
B: 7 students
C+: 2 students
C: 1 student
|
|