|
M 4/2/07
|
No additional HW due today. If you have gaps in your
previous assignments, however, you should patch them up, since any of the old
assignments may be collected or re-scanned.
|
|
|
T 4/3/07
|
HW due: Read §5.5; write §5.4 #26, 28, 52.
|
|
|
W 4/4/07
|
HW due: Use the Integral Approximation Thingy (found on the
HappyCal Zone page, below the schedule) to estimate each of the following definite
integrals by Trapezoid Rule and Simpson’s Rule, 10 intervals for each. Use
MATH 9 to compute the high-precision “true” value, and then compute the
relative errors. Relative error is defined as (estimate – actual)/actual,
expressed as a percentage. The first one is done for you as an example, but
you must rewrite it for full credit. (You will learn more if you also go
through the calculator and computer keystrokes for #1, but unless I stand
over you and watch you, I can’t force you to do that.)
1. 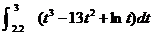
Answer by calc. » –55.704 [use calc. to “STO” the full unrounded value, –55.70383599 . . ., into A]
Estimate by T10 » –55.70833796679351 [“STO” maximum-precision value
into B]
Estimate by S10 » –55.70383601928591 [“STO” maximum-precision value
into C]
T10 relative error = (B
– A)/A » .00808%
S10 relative error = (C
– A)/A » .00000004635%
2. 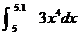
3. 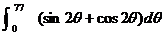
|
|
|
Th 4/5/07
|
HW due: Use the Trapezoid Rule and Simpson’s Rule formulas
manually (i.e., on your calculator) to estimate each of the following
integrals using 7 equally spaced mesh points (i.e., 6 intervals). Show your
calculator work. You may use the Thingy to check your answers. The first one
is done for you as an example, but you need to recopy it for full credit.
Remember, you must show formula, plug-ins, simplifications, and answer.
1. 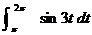
T6 = ½Dt (y0
+ 2y1 + 2y2 + 2y3 + 2y4+
2y5 + y6) for mesh points p, 7p/6, 8p/6, 9p/6, 10p/6, 11p/6, 2p
= ½(p/6) ( sin 3(p) + 2 sin 3(7p/6) + 2 sin 3(8p/6) + 2 sin 3(9p/6) + 2 sin 3(10p/6)
+
2 sin 3(11p/6) + sin 3(2p) )
= ½(p/6) ( 0 + (–2) + 0 + 2
+ 0 + (–2) + 0)
= (p/12) (–2) = –p/6 » –.524
S6 = ⅓Dt (y0
+ 4y1 + 2y2 + 4y3 + 2y4+
4y5 + y6) for mesh points p, 7p/6, 8p/6, 9p/6, 10p/6, 11p/6, 2p
= ⅓(p/6) ( sin 3(p) + 4 sin 3(7p/6) + 2 sin 3(8p/6) + 4 sin 3(9p/6) + 2 sin 3(10p/6)
+
4 sin 3(11p/6) + sin 3(2p) )
= ⅓(p/6) ( 0 + (–4) + 0 + 4 + 0 + (–4) + 0)
= (p/18) (–4) = –2p/9 » –.698
2. 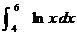
3. 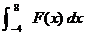 for the quartic
function F tabulated below: for the quartic
function F tabulated below:
|
|
|
|
x
|
–4
|
–3
|
–2
|
–1
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
|
|
F(x)
|
1.88
|
–4.095
|
–5.72
|
–4.495
|
–1.8
|
1.105
|
3.08
|
3.105
|
.28
|
–6.175
|
–16.92
|
–32.495
|
–53.32
|
|
|
F 4/6/07
|
HW due: p. 298 #11ab. Write sentences (in your own words) justifying
what you are doing at each step and why you are doing it. An example is shown
below for the beginning of part (b). You need not use complete sentences,
provided you are clear. However, do use your own words so that you can absorb
the full reality of what is happening.
(b) Since s(0) = v(0) = 0, we know the object is
starting from rest at position 0. At time t
= 2, what is s? We can answer this
by noticing that v(2) = 1. If v(0) = 0 and v(2) = 1, a reasonable estimate for the “average” velocity on the
interval [0, 2] is 0.5 meters per second. (Maybe a little less, because the
curve bends upward, but 0.5 is a reasonable estimate.) Traveling an average
of 0.5 meters per second for 2 seconds gives us an expression for distance
covered:
d = rt » (0.5 m/sec) (2 sec) = 1 m
Common sense therefore tells us that s(2)
» 1 m.
Similarly, the average velocity on [2, 4] is approximately 2 m/sec. (Again,
the true answer is probably a little less, since the curve is concave up, but
2 is a reasonable estimate.) Therefore, during the time interval [2, 4] we
would travel approximately 4 m.
Summary: s(4) » 5 m. [We can’t simply write 4. We have to include
the 1 m calculated above, which gives us a total of 4 + 1.]
Proceeding in this way, we can come up with estimates for s(6), s(8), and s(10). [Now
do it!]
|
|
|
M 4/9/07
|
HW due: Use the STAT EDIT technique on your calculator to
perform a 100-interval estimate of 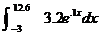 , first using the Trapezoid Rule and then using Simpson’s
Rule. , first using the Trapezoid Rule and then using Simpson’s
Rule.
In other words, you will need to take the interval length (15.6) and chop it
into 100 equal intervals. Store these 101 mesh points into list L1
as –3, –2.844, –2.688, etc. Now, clearly, that is a royal pain to enter those
101 values by hand. Luckily, you can use the calculator command
seq(X,X,-3,12.6,.156)®L1
to do the job for you. Note: The
seq function is found on the 2nd LIST menu, under OPS, and the ® symbol denotes the STO command on your calculator.
After you have created list L1 as described above, use the method
given in class to create L2 with function values. If you missed
class or forgot to take notes, then call a friend. Be resourceful. You might
even (gasp) try reading the manual that came with your calculator.
Put the weights in L3. For the Trapezoid Rule, these are done as
follows:
seq(2,X,1,101,1)®L3
1®L3(1)
1®L3(101)
Now you have a weight of 1 in the first entry, a weight of 1 in the 101st
entry, and a weight of 2 in all the other entries.
Finally, define L4 to be L2*L3, and compute
sum(L4) using the “sum” function found under 2nd LIST MATH. Your
answer is given by the formula ½Dx times that answer.
For Simpson’s Rule, the steps are exactly the same, except that you have a
very tedious step to insert the weights in L3. You can manually
enter 1, 4, 2, 4, 2, 4, 2, 4, . . . . , 4, 1, which is a big nuisance, but it
will be finished in a few minutes, and you can do it while you are watching
TV. Then compute ⅓Dx times sum(L4), and that’s all.
Important: Do not clear your
calculator’s memory. Keep all of your lists in your calculator’s memory so
that I can check them in class. Write up your answers on a standard HW sheet
as always.
1. Give the results for the Trapezoid Rule.
2. Give the results for Simpson’s Rule.
3. Which one do you think is more accurate in this case? Justify your answer.
4. Is Troy’s Integral Approximation Thingy a fairly good program? Justify
your answer.
|
|
|
T 4/10/07
|
HW due: p. 301 #56, modified as described below.
You are the town engineer. Fill dirt is cheap (hence the expression, “dirt
cheap”), but transporting the fill to the swamp site and dumping it in will
cost approximately $40 per cubic yard.
Which of the following budget requests will you submit to the town council
for the swamp-filling project? Justify your answer with 1-2 coherent, legible
paragraphs that include your shown work. Assume that all environmental
permits have already been obtained and that the wet muck has already been
dredged out. You may compare answers with classmates, but the work and
wording shown on your paper must be entirely your own.
(A) $45,000
(B) $65,000
(C) $85,000
(D) $105,000
(E) $125,000
|
|
|
W 4/11/07
|
HW due: Pairs assignments and program requirements are as
shown below. This program must be essentially complete at the start of class,
but we will spend a few additional minutes at the start of class before
grading it. My suggestion is that both people in each pair should use a
personal calculator and then jointly debug whichever of the two versions
works better. If your program is mostly
working correctly, I will be able to assist you much more helpfully than if
you are still stumbling around with entering your program.
Pair 1: Marshall, Gabe (Midpoint Rule and Trapezoid Rule, in that order)
Pair 2: Ali, Bobby (Midpoint Rule and Left Endpoint Rule, in that order)
Pair 3: Jaime, Chris (Midpoint Rule and Right Endpoint Rule, in that order)
Pair 4: Chet, Mark (Simpson’s Rule and Trapezoid Rule, in that order)
Pair 5: Garrett, Max (Simpson’s Rule and Left Endpoint Rule, in that order)
Pair 6: Jamal, Ryan (Simpson’s Rule and Right Endpoint Rule, in that order)
Pair 7: Austin, Henry (Trapezoid Rule and Left Endpoint Rule, in that order)
Pair 8: Evan, Mr. Hansen (Trapezoid Rule and Right Endpoint Rule, in that
order)
Modify the program SAMPLE (see below) so that it meets the requirements shown
above. The sample program implements Simpson’s Rule and the Midpoint Rule.
The user must be allowed to choose between two methods.
Recall (from Precal class) that you can enter a new program by pressing PRGM
and choosing NEW from the menu. Use as your program name the shorter of the
two first names in your group, or the one that is alphabetically first in the
case of a tie (i.e., GABE, ALI, CHRIS, CHET, MAX, RYAN, HENRY, or EVAN).
All commands that you see, such as ClrHome, can be found under the PRGM menus
while you are in programming mode. For example, ClrHome is under the PRGM I/O
menu, which means that you need to press PRGM, highlight I/O, and scroll down
to the 8th choice. To leave programming mode, use 2nd QUIT.
Do not enter the bracketed comments. They are in there simply to make the
program a little easier to understand.
PROGRAM:SAMPLE
:ClrHome
:Disp "INTROCAL PROG."
:Disp "EXERCISE 4/12/07"
:Disp "GROUP MEMBERS:"
:Disp " 1. EVAN"
:Disp " 2. MR. HANSEN"
:Disp "PRESS 'ENTER'"
:Disp "KEY TO GO ON..."
:Pause
:ClrHome
:Disp "FUNCTION MUST"
:Disp "ALREADY EXIST"
:Disp "AS Y1 IN CALC."
:Disp ""
:Disp "PRESS 'ENTER'"
:Disp "TO CONTINUE OR"
:Disp "'ON' TO QUIT..."
:Pause
:ClrHome
:Disp "ENTER THE NUMBER"
:Disp "1 OR 2, PLEASE."
:Disp "1 = SIMPSON'S"
:Disp "2 = MIDPT."
:Input C
:If (C=1) or (C=2) [Warning: “or” must be entered with 2nd TEST LOGIC
menu.]
:Then
:Goto PR
:Else
:ClrHome
:Disp "INVALID CHOICE"
:Stop
:End
:Lbl PR
:ClrHome
:Disp "LEFT ENDPT."
:Input A
:Disp "RIGHT ENDPT."
:Input B
:Disp "NO. OF INTERVALS"
:Input N
:If (N/2=int(N/2)) and (N>0) [Warning: “and” is also on 2nd TEST LOGIC menu.]
:Then
:Disp "PLEASE WAIT..."
:Else
:int(abs(N))+1®N
:round(N/2,0)*2®N
:Disp "ADJUSTING NO. "
:Disp "OF INTERVALS TO"
:Disp N
:Disp "PLEASE WAIT..."
:End
:0®dim(L1)
:0®dim(L2)
:0®dim(L3)
:0®dim(L4)
:(B-A)/N®H [Note that h
is the step size, i.e., what we usually call Dx.]
:For(K,1,N+1,1)
:A+(K-1)H®L1(K) [Place mesh point value into appropriate entry in L1.]
:Y1(L1(K))®L2(K) [Place function value into appropriate entry in L2.]
:End
:If C=1
:Then
:Goto P1
:Else
:Goto P2
:End
:Lbl P1
:1®L3(1)
:For(K,2,N,1)
:If K/2=int(K/2)
:Then
:4®L3(K) [Use weight 4 for first mesh point after a and every second one thereafter.]
:Else
:2®L3(K) [Use weight 2 for most other mesh points,
alternating with 4.]
:End
:End
:1®L3(N+1) [Use weight 1 for the very last mesh point, i.e., b.]
:L2*L3®L4
:1/3*H*sum(L4)®D
:Goto TA
:Lbl P2
:For(K,1,N+1,1)
:L1(K)+H/2®L1(K) [This moves the mesh point slightly forward, by half
the step size h.]
:If K>N
:Then
:B®L1(K) [The last mesh point should not be altered, since
that could make the program crash.]
:End
:Y1(L1(K))®L2(K) [This recalculates the function value, since the
mesh point has moved.]
:1®L3(K)
:End
:0®L3(N+1) [We must reset the very last weight to 0, since the
(n+1)st mesh point is not used.]
:L2*L3®L4
:H*sum(L4)®D
:Lbl TA
:ClrHome
:Disp "THE DEFINITE"
:Disp "INTEGRAL IS"
:Disp "APPROXIMATELY"
:Disp D
|
|
|
Th 4/12/07
|
HW due: Try to finish your pairs project. However, I have
agreed to extend the deadline by one day, until tomorrow. If you have a draft
writeup to show me, I will be happy to look at it and give you an estimate of
how far short of an A it falls. That way, you will still have time to make
modifications and earn a good grade.
|
|
|
F 4/13/07
|
HW due: Pairs project is due in final form by 3:30 p.m.
Your submission must consist of the following components.
1. Title page, signed by both members of the pair.
2. Program listing. (You can use the Math Lab computers to copy and paste
your program code so that you do not have to retype it.)
3. Proof of proper operation. This should consist of two tables of examples
calibrated against Troy’s Integral Approximation Thingy or another suitable
program. You will need one table for each of the two types of integral that
your program is supposed to be able to calculate, columns for a, b,
n, y, target output, and actual output, and enough rows to
demonstrate that you have tested a good variety of possible situations. For
example, you need to show that your program works correctly even if a or b is negative, even if h
< 0, and even if n is rather
large. If n is too large, you will
exceed the memory of your calculator.
Scoring: 60 points (30 points per student) if all components are present,
clearly and neatly shown. Extra credit if you improve the error checking so
that the program is less likely to run out of memory.
|
|
|
M 4/16/07
|
HW due: Read from middle of p. 306 to the heading,
“Applications,” on p. 309; write §6.1 Exercises #1-16 all, 18-24 even.
Remember that for full credit, you must state the setup of the problem. You
may not simply write the answer. See #17 below, which is worked for you as an
example. There is no work to show, since the antiderivatives can be found by
inspection, but you must still state the setup of the problem.
17. 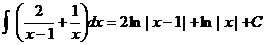
In class: Quiz on the Lessons from
the Pentagon. You will not be required to memorize these, but you must be
able to answer questions that demonstrate that you know the principles
involved. Some sample questions are given below. If you want to know the
correct answers, send me an e-mail with your guesses, and I will respond.
1. If you have a major beef with a coworker, you should begin by . . .
(A) speaking directly with him or her
(B) speaking with your supervisor
(C) speaking with your other coworkers
(D) saying nothing and allowing the stress to consume you from the inside
(E) A or D
2. You are a mid-level manager for a small startup tech firm in Vienna, VA.
You have personally never been featured in a newspaper or magazine article. A
magazine reporter contacts you to confirm some facts and shares a portion of
the article with you before publication. You notice that your name is
misspelled, and the reporter agrees to make the correction along with several
other minor factual corrections. The reporter circulates a corrected excerpt
to you as a courtesy, and you read and approve it. However, when the article
appears in print, you notice that the factual content of the article is
correct, but your name is once again misspelled. What is the most likely
explanation?
(A) Your name is misspelled in the magazine’s style guide.
(B) The reporter is deliberately displaying disrespect toward you and/or your
company.
(C) A version control slipup occurred.
(D) The reporter never actually corrected the spelling of your name.
(E) Your name was misspelled on the second copy you saw, but you did not
notice the error.
3. Your latest project assignment has been given to you, with a deadline 30
days in the future. After a few days of hard work, you can see that you will
not be able to meet the deadline subject to the stated project scope and
budget. How do you proceed?
(A) Immediately negotiate a new deadline.
(B) Immediately negotiate a new deadline, a new scope of work, or a new
budget.
(C) Double your work effort right up until the deadline, and then negotiate a
new deadline.
(D) Make a case for a reduction in the scope of the project.
(E) Spend your entire budget early so that your boss will be forced to fund
your project at the correct level.
|
|
|
T 4/17/07
|
HW due: §6.1 #25, 26. The word “solution” means a function whose derivative is as stated
and whose value at the given x-value is as stated. This meaning of the
word “solution” is different from what you have seen in previous math classes
and should be learned and memorized. (Hint, hint.)
For example, the solution to the initial value problem dy/dx = 2x, y(0) = 4 is the function y = x2 + 4.
Check: If y = x2 + 4, then dy/dx = 2x as stated, and y(0) =
02 + 4 = 4 as stated.
Next example: The solution to the initial value problem dy/dx = 1/x, y(2)
= 7 is the function y = 7 – ln 2 +
ln x.
Check: If y = 7 – ln 2 + ln x, then dy/dx = 1/x as stated, and y(2) = 7 – ln 2 + ln(2) = 7 as stated.
|
|
|
W 4/18/07
|
HW due: Answer the following questions. For questions
involving a fill-in, write the entire sentence, underlining the word or
phrase that needs to be filled in.
1. Sketch the relation x2
+ y2 = 16, showing all x-intercepts and y-intercepts. Hint:
This is one of the easier types of conic sections. The radius is the square
root of 16, namely 4.
2. Use algebra to solve the relation in #1 for y. You should get two
answers, which represent an upper semicircle and a lower semicircle. Label
your two answers as y1
and y2. Show all of your
algebraic steps.
3. Store y1 and y2 into your calculator as
two functions. Press ZOOM 6 and sketch the resulting plot on your paper.
4. Write the sentences and fill in the blank: “The plot does not look like a
circle because (1) the aspect ratio is wrong, since horizontal and _______
distances are not equal on the calculator plot, and (2) the endpoints ______
and ______ are missing. The reason that the endpoints are missing is that the
calculator is a _______ device that plots only a certain number of pixels,
and as luck would have it, there is no pixel that corresponds to (–4, 0) or
(4, 0).”
5. If we are clever, we can set the calculator window so that (–4, 0) and (4,
0) will correspond to pixels. To do
this, press WINDOW and set the window range to [–4.7, 4.7] ´ [–4, 4]. If you have forgotten what this notation
means, please ask a classmate. We covered this last fall. Sketch the new plot
that you get.
6. Use common sense (not MATH 9) to compute 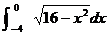 . Hint: This is
the upper left quarter circle. Show your work. . Hint: This is
the upper left quarter circle. Show your work.
7. Now use MATH 9 to answer #6. How many seconds does your calculator take to
get an answer?
8. Write the sentence and fill in the blank: “The reason that the calculator
takes so long to compute #6 is that the calculator’s
__________ __________ algorithm requires a very small ______ size
near the left endpoint, an area where the __________ has a large absolute
value.”
9. Use MATH 9 to compute 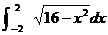 . In your own words, describe
and explain what you notice. . In your own words, describe
and explain what you notice.
10. Sketch the relation (x – 2)2
+ (y + 3)2 = 13, showing
all x-intercepts and y-intercepts in their approximately
correct locations.. Hint: This is
one of the easier types of conic sections. The radius is the square root of
13, or approximately 3.6.
11. Use algebra to solve the relation in #10 for y. You should get two
answers, which represent an upper semicircle and a lower semicircle. Label
your two answers as y1
and y2. Show all of your
algebraic steps.
12. Store y1 and y2 from #11 as two
functions. Use the window [–7.4, 11.4] ´ [–9.2, 3.2] to graph the relation, and sketch your
results.
13. Prove algebraically that (0, 0) is a point on the relation. Show your
work.
14. Use common sense (not MATH 9) to compute 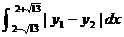 . .
15. Use MATH 9 to answer #14. Explain in your own words why the running time
is so long.
|
|
|
Th 4/19/07
|
No additional HW due.
|
|
|
F 4/20/07
|
HW due: Use Appendix A7 (pp. 628 et seq.) to find the
following. Show formula, plug-ins, and simplified answer.
1. 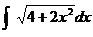
2. 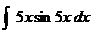
3. 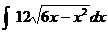
4. 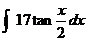
5. 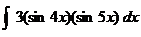
|
|
|
M 4/23/07
|
Phi Beta Kappa Day (no school).
|
|
|
T 4/24/07
|
No additional HW due. Hooray! Please use this time
to rest, relax, recharge, and get caught up on previously assigned HW if
necessary.
|
|
|
W 4/25/07
|
HW due: Read all of §6.1. Reading notes are required, as
always. If there is a reading comprehension quiz (for example, on
terminology), you may use your reading notes.
|
|
|
Th 4/26/07
|
HW due: Use the BIGSLOPE program distributed in class to
make a slope field for the diff. eq.
dy/dx + x + 2y = xy/3.
(If you were not in class, then either do the plotting by hand, which is
fairly easy, or come in early to get a copy from me or from a classmate.)
1. Use the window [–6.5, 5.5] ´ [–4.5, 3.5], and transcribe the results neatly onto
your homework sheet. Hint: It helps
to use the setup command to turn the axes on so that you can tell where the
lattice points are.
2. Sketch the solution that satisfies the initial condition y(–1) = 0.
3. Use your answer to #2 to predict y
when x = –2.
4. Sketch the solution that satisfies the initial condition y(–1) = 1.
5. Use your answer to #4 to predict y
when x = –2.
6. Compare your answers to #3 and #5. What can you conclude about the
importance of measuring initial conditions accurately?
7. What adjective do we apply to a region of a slope field that has the
property that any change in the
initial conditions, no matter how small, causes a large change in the
solution track?
8. Does the slope field you plotted have the property described in #7?
Explain briefly.
9. In your own words, write a paragraph in which you speculate on the
possible real-world value of slope fields and solutions to differential
equations.
|
|
|
F 4/27/07
|
No class.
|
|
|
M 4/30/07
|
HW due: Write p. 313 #43, 44, 49. Working with classmates is
encouraged but not required. However, each student must produce his own
writeup. In parts (a) and (b) of #49, change the word “find” to “sketch.” In
#49(c), remember that showing that a solution works means you must compute dy/dx
(implicitly, if necessary), and verify that your answer agrees with the claim
made by the original diff. eq. If it does, you must show that this is the
case, and then write a check mark.
|
|