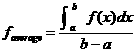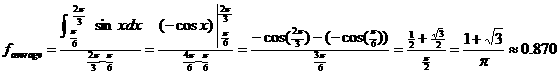|
Th 3/1/07
|
HW due: §5.2 #13-27 odd. Work (including a sketch in most
cases) is required. Check your answers in the back of the book and/or by using
MATH 9. The style of solution is illustrated on p. 750 for #13. Use that
style of solution throughout.
In class: Second viewing of the tenth dimension video.
|
|
|
F 3/2/07
|
HW due: Read §5.3; write §5.2 #41-46 all.
Note for #41-42: Be sure to show the setup using integral notation. (No
credit for answer without setup.)
Note for #43-46 all: Use MATH 9 to double-check your answers. Graphs are
required for each one, and your point(s) of discontinuity should be clearly
shown.
Note for #44: The “int” function is referring to the greatest integer
function, which can be found on your calculator under 2nd CATALOG. The
notation int(x) means the greatest
integer less than or equal to x.
For example, int(3.218) = 3, int(–5.118) = –6, int(7.9999) = 7, and int(k) = k whenever k is an
integer.
|
|
|
M 3/5/07
|
Double
Quiz on FTC and area calculations
using definite integrals, including MATH 9.
There is no additional written work due today.
|
|
|
T 3/6/07
|
Oops! No additional HW since it was not posted in
time. If you wish, you may read pp. 268-274, which we started to cover
yesterday in class.
|
|
|
W 3/7/07
|
Quest (70 pts.) on FTC, Definite Integrals, and Optimization. If for some reason school is canceled today, the
quest will be provided to you as a take-home quest due Thursday.
Mean value of a function (yellow box on p. 271) will also be on the quest.
See §5.3 #25-29 for examples of problems of this type. Since the mean value
formula has not been covered in class, it will be provided for you.
Example problem:
Compute the average (mean) value of the sine function over the interval [p/6, 2p/3] by applying the formula 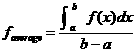 . Use FTC, showing your work, and check your answer. . Use FTC, showing your work, and check your answer.
Solution:
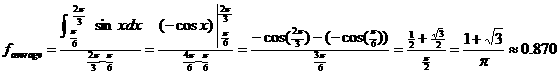
Check: MATH 9 sin(x),x,p/6,2p/3 gives 1.366 . . . , which yields 0.870 when divided by (2p/3 – p/6). ü
|
|
|
Th 3/8/07
|
HW due: Read pp. 268-274; rewrite questions #1-5 from yesterday’s quest. On a separate sheet of paper,
write question #6 from yesterday’s quest.
You may work together on #1-5 but not on #6. If you wish to have #6 graded
and attached to your quest score, you must sign a statement at the top of
your #6 sheet saying that you worked alone on the problem. (Otherwise, the
problem will be scored only as homework, and the quest will be scored as
originally submitted.)
The answer to #6 is approximately 26.5 units, but you get no credit for that
answer. You need to show work supported by integral(s). A diagram is strongly
suggested. As always, your final answer must be correct to at least 3 decimal
places.
|
|
|
F 3/9/07
|
Last day of quarter. We celebrate by having no
additional HW due. Hooray!
|
|
|
M 3/12/07
|
Form VI Career Day—class canceled for everyone.
|
|
|
T 3/13/07
|
Quiz (10
pts.) on the rules on p. 269 and
the yellow box on p. 271.
No additional HW due today. However, be sure you have read pp. 268-274 if you
have not already done so. Reading notes are required, as always.
|
|
|
W 3/14/07
|
HW due: §5.3 #2, 4, 6, 25-28 all.
|
|
|
Th 3/15/07
|
HW due: Read §5.4, especially Example 4 and the top half of
p. 280 (up to the boldface subheading). Written assignment:
1.(a) First, note that on p. 282, the statement that your book calls FTC2
(which we learned previously) is proved by means of FTC1. In fact, the very
first sentence in the proof says “Part 1 of the Fundamental Theorem tells us
. . .” We may summarize this proof by saying that the truth of what your book
calls FTC1 allows us to prove the truth of FTC2. In other words, FTC1
implies FTC2. Write this, using mathematical notation.
(b) Prove that FTC2 implies FTC1. In other words, show that if you
take the entire yellow box on p. 282 as a given (which should be easy to do,
since you have been quizzed on this several times and know it thoroughly by
now), then the equation at the end of the yellow box on p. 277 is true. Do
not use the proof that your book gives you on pp. 277-278, which is long and
difficult. Use a simpler approach that takes advantage of the FTC that you
already learned. Your proof should be no more than about 4 lines long. Give a
reason for each step.
If the word “prove” frightens you, then start with the expression 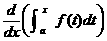 and simplify it. and simplify it.
Your goal is to obtain f (x) by providing a valid reason for
each step.
(c) The outcome of part (a) is that FTC1 Ž FTC2. The outcome of part (b), whether you were
successful or not, is that FTC2 Ž FTC1. What do (a) and (b) say, if you take them
together as a pair?
2. Yesterday’s assignment may be collected and scanned a second time. Do not
throw away points!
|
|
|
F 3/16/07
|
HW due: Do all 7 problems, even #1. For #1, all you need to
do is copy my work for the two solution methods, but you must do both of
them.
1. Find a function G(x) whose derivative is e3x if it is given that G(2.3)
= –1.8.
Solution: By FTC1, e3x has an antiderivative, namely 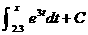 . .
The lower limit of integration is chosen to make our lives easy, and the
required value of C is clearly
–1.8, since an integral from 2.3 to 2.3 is 0. With practice, we can solve
problems like this by inspection. Answer: 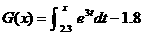 . .
Solution (alternate method): A general antiderivative of e3x is 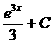 . Plug in x = 2.3
and write . Plug in x = 2.3
and write
the equation that must be true: 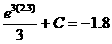 . By simple algebra [show the steps when . By simple algebra [show the steps when
you write this up], C » –332.558. Final answer: 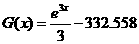 . .
2. Explain why method 1 for #1 is better. Hint:
Think of what might happen if the given derivative was something for which
one could not easily find an antiderivative by the techniques we learned
earlier in the year.
3. Find a function H(x) whose derivative is sin x if it is given that H(–11) = –3.18. Use both methods.
4. Find a function K(x) whose derivative is cos2
x if it is given that K(3.17) = 11.458. Use whichever method
you prefer.
5. Find a function L(x) whose derivative is tan xln x if it is given that L(4)
= 8. Use whichever method you prefer.
6. Find a function M(x) whose derivative is 7x cos x if it is given that M(2.99)
= p. Use whichever method
you prefer.
7. I am thinking of a function N(x) whose derivative is –15ecos x + 2. I will tell you that N(3) = 7.188. Problem: Find N(3.2).
Hint for #7: First, find N(x).
Then, use your calculator to plug in and find N(3.2).
|
|