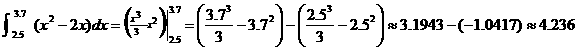|
Th 2/1/07
|
HW due: Read §4.3, virtually all of which consists of
material previously discussed in class. Because I am interested in whether
you have the ability to take good notes, there will be a Quiz to determine basic awareness of the essential ideas in the
section. For example, I might ask for an example of an S-shaped curve that
provides an opportunity to find a point of inflection, and you might recall
the logistic curve example
mentioned in the text on p. 200. (You would know that the shape is an S only
if you had actually punched the buttons on your calculator in order to
execute the answer to part (a), of course.)
|
|
|
F 2/2/07
|
No additional HW due. There may be another open-note
quiz similar to yesterday’s.
|
|
|
M 2/5/07
|
HW due: §4.3 #7-10 all. Today is a normal class period
(meet in hallway across from Room R). Anyone taking a cut or a skip today
should e-mail his HW by no later than noon today. Remember to put a double underscore
at the beginning of your subject line. In your e-mail, you may omit the
graphs, and you may be creative in your typographical approach. For example,
here is how you might write up #11 for e-mail:
11. y = x sqrt(8-x^2) = x (8-x^2)^(1/2)
First, note that the domain of the fcn. is
[-sqrt(8), sqrt(8)].
y' = x(1/2)(8-x^2)^(-1/2) (-2x) + (8-x^2)^(1/2)
= sqrt(8-x^2) (1-(x^2)/(8-x^2))
Note that the domain of y' is the open interval
(-sqrt(8), sqrt(8)), not the closed interval.
Observe how the deriv. can be expressed as a
product of two factors. The first factor,
namely sqrt(8-x^2), is >0 whenever
0<x<sqrt(8) or -sqrt(8)<x<0.
The second factor, namely (1-(x^2)/(8-x^2)), is
>0 whenever -2<x<2 but
is <0 whenever x>2 or x<-2. In
summary, we have the following:
x = -sqrt(8)
==> y'=0
-sqrt(8)<x<-2
==> y'=(pos.)(neg.)<0 ==> y is decreasing
x=-2 ==> y'=0
-2<x<0
==> y'=(pos.)(pos.)>0 ==> y is increasing
x=0 ==> y'=0
0<x<2
==> y'=(pos.)(pos.)>0 ==> y is increasing
x=2 ==> y'=0
2<x<sqrt(8)
==> y'=(pos.)(neg.)<0 ==> y is decreasing
x= sqrt(8) ==>
y'=0
Now, calculate y'' using the revised version of
y' from above, namely y'= sqrt(8-x^2) (1-(x^2)/(8-x^2)).
We have y''=
-sqrt(8-x^2)((2x(8-x^2)+2x^3)/(8-x^2)^2) - (x/sqrt(8-x^2))(1-(x^2)/(8-x^2)).
After some simplification [steps omitted for
e-mail], we have y''= -(3x+(x^3)/(8-x^2))/sqrt(8-x^2).
For negative values of x in the interior of the
domain, we have
y'' = -(neg. +
neg./pos.)/sqrt(pos.) = -(neg./pos.)>0.
For positive values of x in the interior of the
domain, we have
y'' = -(pos. +
pos/pos.)/sqrt(pos.) = -(pos./pos.)<0.
Answers (note that book’s answer key is not
completely correct):
(a) fcn. is increasing on (-2, 0) and (0, 2)
(b) fcn. is decreasing on (-sqrt(8), -2) and
(2, sqrt(8))
(c) fcn. is concave upward on (-sqrt(8), 0);
y'' is undefined at x=-sqrt(8)
(d) fcn. is concave downward on (0, sqrt(8));
y'' is undefined at x=sqrt(8)
(e) Fcn. has local max at (-sqrt(8), 0) since y
is decreasing to the right of this endpt.;
fcn. also has
local max at (2, 4) by applying either the 1st deriv. test or 2nd deriv. test.
Fcn. has local
min at (sqrt(8), 0) since y is decreasing to the left of this endpt.;
fcn. also has
local min. at (-2, -4) by applying either the 1st deriv. test or 2nd deriv.
test.
(f) Since fcn. is cont. at (0, 0) and y''
changes sign there, (0, 0) is a pt. of inflection.
(g) [Graphical support for answers is shown on
HW paper but omitted for e-mail.]
The four problems I have assigned you, namely #7-10, are easier than #11
(thank goodness!) because the derivatives and second derivatives are not as
messy. However, you still need to perform careful analysis of the signs of
the first and second derivatives, as shown in the example above.
|
|
|
T 2/6/07
|
HW due: Re-do yesterday’s assignment correctly.
I received two submissions yesterday. One was fairly good, missing only the
graphs and some of the justifications of maxima and minima, and the other
basically needed to be redone from scratch. I decided to award bonus points
unequally to those students. Everyone needs to do this assignment. If you
need hints, please contact me or read through the example for #11 above.
Remember, you do not earn any credit simply by copying the book’s answers.
First of all, some of the book’s answers are incorrect. Second, the book does
not identify the setup of the problem in the answer, which is a requirement
of the standard HW format. At a minimum, for example, writeups to #7ab would
have to resemble the following:
7.(a) y = x2 – x – 1 Þ y¢ = 2x – 1
Thus y¢ > 0 means 2x
– 1 > 0 Û x > ½.
Answer: y is increasing on (½, ¥). [The book’s answer is incorrect.]
(b) Similarly, y¢ < 0 means 2x
– 1 < 0 Û x < ½.
Answer: y is decreasing on (–¥, ½). [Again, the book’s answer is incorrect.]
|
|
|
W 2/7/07
|
HW due: §4.3 #7-10 all. That’s right! We’re not proceeding
until a majority of the class can get this. The quality standards are higher
today, and I recommend that anyone with a score of 2/4 or below should simply
start over. Rough sketches are still acceptable for your graphs.
The issue is not whether you can obtain the answers, since all of the
problems except #10 are easy enough that you can practically read the answers
off the graphs. The issue is whether you can apply a systematic, analytic
procedure to demonstrate to a reader that your answers are supported by
careful, disciplined work.
There is a life skill here that applies far outside the realm of mathematics.
If you are a lawyer, a doctor, a CPA, an investment manager, or even an
assistant manager of a McDonald’s, much of your working life will consist of
following procedures and documenting that you followed the procedures. You
might as well learn now how to do that. I admit that the current problems are
in a more abstract realm. Nevertheless, the reason (in most cases) that the
previous HW submissions were unacceptable was not because of a lack of
understanding. Rather, it was that insufficient work was shown (“NSW”) or
that the answers were not supported by the work that you did show (“NSBW”).
[For a list of all symbols and abbreviations that I use, please see Mr. Hansen’s abbreviations page.]
In an attempt to help you systematically and analytically
answer the questions, I offer the following “road map” for each of the problems:
(before starting) Compute y¢ and y¢¢ so that you have them for later reference.
(a) Where is y¢ > 0? Solve the inequality, using your precal skills. You almost
always need to do some factoring and/or algebraic manipulation. It is not
acceptable to “eyeball” the regions from a graph. Show your work.
(b) Where is y¢ < 0? Same comments as in part (a).
(c) Where is y¢¢ > 0? Same comments as in part (a).
(d) Where is y¢¢ < 0? Same comments as in part (a).
(e) Where is y¢ = 0 or undefined (for points in the interior of the domain)? These
are called critical points. Test
each one, using either the 1st deriv. test or the 2nd deriv. test, to see
whether it is a min., a max., or something else. Show your work as you apply
the tests. Label your answer(s) according to type (local min., local max.,
etc.) and write them as ordered pair(s), plugging in to find y if necessary. [Remember that the 2nd
deriv. test, though preferred by most students, is sometimes inconclusive.
Luckily, we do not have to deal with that situation today, since the 2nd
deriv. test does the job nicely for problems #7-10. We will deal with the
complications of an inconclusive 2nd deriv. test some other day, maybe when
the weather is warmer and we are all feeling a bit cheerier.]
(f) Refer to your answers to parts
(c) and (d) in order to see the place(s) where y¢¢ has undergone a sign change. If any of these is at a place where y is continuous, then you have found a
point of inflection. Document the sign change in some readable fashion,
and write your answer(s) as ordered pair(s), plugging in to find y if necessary. [If there is no sign
change (as is the case for #7), then state that there is no sign change for y¢¢ and hence no point of inflection for the function.
For full credit, you cannot simply write, “No inflection point.”]
Full sentences are not required. Full thought is required, however. If you
have trouble finding y¢ and y¢¢ in #10, call a friend for help. If you send me an
e-mail with your guesses, I will tell you whether you are right or wrong.
|
|
|
Th 2/8/07
|
HW due: §4.3 #10. I said during class that there would be a
few more problems, but this is enough for now. Make sure you have clean,
factored versions of y¢ and y¢¢ before answering parts (a) through (f). Call a
friend for help if necessary.
|
|
|
F 2/9/07
|
HW due: Read first 3 pages of §4.4 (pp. 206-208 only);
write §4.3 #41, 42, 48.
|
|
|
M 2/12/07
|
HW due: Carefully read the paragraphs below; then use the strategy
at the bottom of p. 208 to write §4.4 #9, 14. This is a double homework scan.
The answers by themselves are not
worth anything. After all, the answers to #9 are already given in the
back of the book, and the answers to #14 are easy to compute with a graphing
calculator. Instead, points will be
awarded based on the quality of your writeup. Show your steps. Neatness
counts. Each problem requires a sketch of the situation, plus a graph
of the relevant mathematical model (function) that you are minimizing or
maximizing.
Follow this format as you state each problem:
[action] [function] s.t. [constraints]
The letters “s.t.” mean “subject to” or “such that.” For example, if the
problem asks you to minimize a volume that depends on height h, where h can be any number in the open interval (0, 4), you would write
Minimize V(h) s.t. 0 < h < 4.
If the problem asks you to maximize an area that depends on time t, where t can be any number in the interval (0, 5], then you would write
Maximize A(t) s.t. 0 < t £ 5.
If the problem asks you to minimize a total cost that depends on unit
production cost u, where u can be any number in the interval
[100, ¥), then you would write
Minimize C(u) s.t. u ³ 100.
If the problem asks you to maximize the profit P that results from regional sales S, where S can be any
number in the interval [0, 6000], then you would write
Maximize P(S) s.t. 0 £ S
£ 6000.
Is the requirement clear? If not, please send me an e-mail. State each
problem using the format illustrated above, and follow the rest of the steps
given in the strategy at the bottom of p. 208.
Notes for #9: I gave you this
problem because it has something of a “real-world” flavor to it. However,
several aspects are unrealistic and potentially confusing.
(1) First, you have to assume that the river is straight, at least in the
vicinity of your land. I know of few rivers that run perfectly straight for
hundreds of meters, but hopefully you can accept the assumption as a
necessary simplification in order to begin the problem. Therefore, in your
sketch, draw a straight river with a rectangular plot on one side of it. Have
you done that? Good.
(2) Second, this problem asks you to accept that the rectangular plot to be
fenced has unknown length and width. This is crazy! If you know anything
about real estate, you know that most plots of land are not rectangular, but
even when they are, the one thing
you would certainly know would be the dimensions of your own land. After all,
you would be trespassing on someone else’s land if you started stringing
fence willy-nilly. All right. Take a deep breath and accept that in “Textbook
Land,” the plot is perfectly rectangular with unknown width and unknown
length.
(3) How many independent variables are there? Most students will say, “Mr.
Hansen, there are two: one for width and one for length.” While that is true
(more or less), it is of no use in solving the problem. In high school
calculus, you see, our techniques for maximizing or minimizing allow only one independent variable. Therefore,
we must mark the diagram using only one
independent variable. How do we do this? On the sketch that you made
earlier, you need to mark one of the dimensions (length or width, take your
pick) as x because it is unknown.
Then mark the other dimension, after some thought, by using an expression
involving x. (You can do this if
you remember the total amount of fencing available.) This is a bit like those
problems you did in Algebra II or Geometry that said something like, “The
perimeter of a rectangle is 10. The width is w. Find the length.” If you could solve problems like that, then
you can figure out how to mark the other unknown dimension in problem #9 as
some expression involving x. The
technique is similar enough that you should be able to do it. (You did pass
Algebra II, after all.) Contact a classmate or e-mail me if you cannot find
an expression for the other unknown dimension. You may temporarily use another letter (such as y) to refer to the other dimension if you wish, but you cannot
proceed until you convert everything in the diagram to be an expression
involving x.
(4) In order to earn points, you must state the problem using the [action]
[function] s.t. [constraints] format given above, and you need to show your
work using the strategy at the bottom of p. 208. Non-calculus methods (e.g.,
“guess and check”) may produce correct answers but will not earn points.
Notes for #14:
(1) Is it obvious that the independent variable is t? When you take derivatives and start hunting for critical points,
you will be taking the derivative with respect to t. In that sense, #14 is the easier of the two problems, because
the problem is already stated in terms of one independent variable.
(2) I realize, since I was once a student, that you will feel tempted to find
the answers to part (b) quickly by using your graphing calculator. Although
that is fine as a double-check, answers found in that way do not qualify for
points. You need to state the problem using the [action] [function] s.t.
[constraints] format given above, and you need to show your work using the
strategy at the bottom of p. 208.
(3) For part (c), you do not need to show your work for finding the two
values of t that make s = 0. It is presumed that you would
either use the quadratic formula (slow, painful) or your graphing calculator
(speedy, joyous). However, you do need to state your t values and show the calculus work involved in finding the
corresponding velocities.
|
|
|
T 2/13/07
|
HW due: §4.4 #19abcde, 33ab.
Hints for #33: Use the illustration
immediately above the problem, which applies to both #32 and #33. Recall from
Algebra II that the general equation is S
= kwd3, where S = stiffness in some unspecified
units, k is an unknown constant
(you can assume k = 1 as in part (b)),
w = width, and d = depth. You will have to use some suitable method from
Geometry class to figure out how to write d
in terms of w, because otherwise
you would have 2 independent variables. Write
Minimize S(d) = kwd3 s.t. 0 < w < 12
before you begin.
|
|
|
W 2/14/07
|
Ice storm (no school).
|
|
|
Th 2/15/07
|
HW due:
1. Finish Tuesday’s assignment if you have not already done so. Especially
with an entire snow day to work on this, there should be no question that you
need to have this problem finished.
2. Carefully propose at least one experimental research question that does
not duplicate any of the ideas proposed yesterday in class. No credit will be
awarded for observational study proposals. If you wish to work with others,
you may submit group proposals, as long as the number of submissions equals
or exceeds the number of people in your group. (For example, a group of 3
would need to submit at least 3 usable questions.) If you do a group
submission, all group members must sign a statement certifying that they
worked together and that everyone pulled his weight. Put the statement and
signatures near the top of your paper. I don’t want someone generating
several ideas and then offering to take on several slackers as a public
service.
Phrase your research proposal in the form of a question. Examples are listed
below. Although most of these are still fair game for your project groups to
work on, you may not use them for today’s HW submission, nor may you use any
of the other examples that were proposed yesterday in class.
When offered a choice of fragrances
(double-blind), what do males choose, and what do females choose? (Note:
This is actually more like an observational study than an experiment, but I
will allow it if the methodology includes some subjects who receive duplicate
fragrances as a way of gauging their ability to distinguish.) Which treat do dogs prefer under
controlled conditions? (Same comment.) Does talking about a quiz after the quiz affect performance on a
future quiz? Does background music affect concentration and/or memory? Does
the temperature in a room affect quiz performance? Do multiple-choice
patterns, possibly including visual patterns, affect scoring? Does
gum-chewing affect perceived attractiveness?
|
|
|
F 2/16/07
|
No school.
|
|
|
M 2/19/07
|
No school.
|
|
|
T 2/20/07
|
HW due: Read this
article from the latest issue of New
York magazine; write §4.4 #48.
Hint for part (a): Be careful to
distinguish between r and r0. Remember that c and r0 are constants, while r is the independent variable and v is the function to be maximized. (It is as if r plays the role of x, and v plays the role of y.)
If this is too confusing for you, you may apply the simplifying assumption in
part (b), namely that r0
= 0.5 and c = 1, to part (a) as
well. You must show your analytic work; a graph is not sufficient proof.
Hint for part (b): Sketch your
graph and answer the question posed by stating whether the claim is supported
or refuted by the graph.
|
|
|
W 2/21/07
|
Double HW
due: Write §4.4 #49, and repeat
§4.4 #48 from scratch, even if you earned 4/4 on yesterday’s assignment.
(Please check your mailbox.) This time, do #48(a) wlog,
in other words without assuming that r0
= 0.5 and c = 1. Find the critical
points analytically, e.g., by using the quadratic formula method illustrated
yesterday in class. Remember that the second derivative test does not help
you here, because you are looking for an absolute
maximum, not a local maximum. (Many of you ran the risk of suboptimizing
yesterday.) Remember that in part (b), a sketch is required in order to
receive credit.
As for #49, the answer is in the back of the book, but there is no credit
without suitable work.
|
|
|
Th 2/22/07
|
HW due: pp. 242-243 #31-35 all.
|
|
|
F 2/23/07
|
Double
Quiz (one on optimization, one on
classroom listening).
HW due: p. 244 # 54, 55.
|
|
|
M 2/26/07
|
No additional HW due. Enjoy your weekend, but make
sure you are caught up on all previously assigned problems. For example,
since your textbook provides a step-by-step procedure on p. 208 for solving
optimization problems, you need (at a minimum) to show evidence of having
performed those steps in order to claim credit for an optimization problem.
Some of the work I saw last week fell short of the mark.
|
|
|
T 2/27/07
|
HW due: Read pp. 261-265, and prove that you know what
Example 4 is talking about by being prepared to produce the answer to any
problem of comparable difficulty on your calculator within 30 seconds. (Time
yourself.) For example, 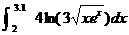
requires keystrokes MATH 9 4ln(3Ö(xe^x)),x,2,3.1 and gives an answer of approximately
12.486. You will need to practice in order to build your speed and
proficiency. Thirty seconds means that you can’t be fumbling around looking
for keys on your calculator. For example, you need to know by heart where the
X key and the comma keys are.
|
|
|
W 2/28/07
|
Quiz (10 pts.) on statement of the first version of FTC.
(We will omit the second version for now.) The theorem states that if a
function f is continuous on [a, b],
and if F is an antiderivative of f (or you can write F ¢ = f to
save writing), then 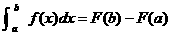 . You need to know the conditions about continuity and the
antiderivative F as well as the
equation itself. . You need to know the conditions about continuity and the
antiderivative F as well as the
equation itself.
Example of an acceptable student response:
“If f is cont. on [a, b]
and F(x) is some antiderivative of f
(x), then 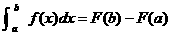 .” .”
Example of an unacceptable response:
“If f is a function and [a, b]
is an interval, then 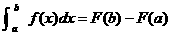 .” .”
HW due: Use the FTC to compute each of the following, and then use your
calculator to check your answer. Include the first two, even though they are
already done for you as examples. You need to show the amount of work that
is shown below in order to obtain full credit. Note that the
vertical-bar notation is sometimes used to indicate “evaluate between these
endpoints.” Do not round any intermediate results. Final answers should be
correct to at least 3 places after the decimal point.
1. 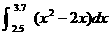
Solution: 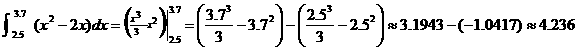
Check: 4.236 by MATH 9.ü
2. 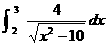
Solution: DNE since integrand is not cont. on [2, 3].
3. 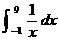
4. 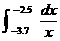
5. 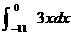
6. 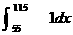
7. 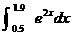
8. 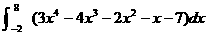
|
|