|
W 11/1/06
|
HW due: Solve the radar-baseball problem using (1)
trigonometry with an interval of 0.003 sec. and (2) the calculus “textbook” method
illustrated in class yesterday. For #2 it is acceptable to recopy your class
notes, provided you do that neatly.
Hint for method (1): Use
trigonometry to compute BR at time t
= 0. Then use common sense to compute the length of BR at time t = 0.003. (Show your work.) From
these facts and the ____________ Theorem (fill in the blank), you should be
able to compute BH at time t = 0
and t = 0.003. Then you can compute
a ____________ quotient to estimate the rate at which BH is changing. (Fill
in the blank.)
|
|
|
Th 11/2/06
|
Notice! In order to celebrate “Fun Friday on Thursday” in
style, with a bit of food (if you bring some to share), we will meet in
Steuart 101 instead of our usual room.
HW due: p. 130 #10, 11, 12, 15. The word “marginal” means “derivative” in
this context. In other words, compute the derivative and evaluate at the
points in question. In #15, the term NDER is meant to refer to your
calculator’s nDeriv(Y1,X,X) function.
After HW check for last 2 days: “Fun Friday on Thursday.”
|
|
|
F 11/3/06
|
No
school.
|
|
|
M 11/6/06
|
No
additional HW due.
In class: Emergency substitution by Mr. Kelley on derivatives and
antiderivatives.
|
|
|
T 11/7/06
|
HW due: §4.3 #1-9 all, 31, 32. You may work in groups for
#31 and 32 if you wish.
Helpful reminders: An extreme point is a point whose
function value is greatest (or tied for “greatest”), or least (or tied for
“least”), among all points in a small open interval. See Figure 4.4 on p. 179
for clarification. An inflection point
is a point of continuity for function f
at which f ¢¢ changes sign. Note that this definition of
inflection point differs somewhat from your book’s definition on p. 198.
|
|
|
W 11/8/06
|
HW due: Read §3.3.
In class: Evan’s group will present §3.3. Pay attention, since there may be a
quiz at the end.
|
|
|
Th 11/9/06
|
Quiz after Bobby’s presentation. Make sure you know §3.3 well.
|
|
|
F 11/10/06
|
No
additional HW due.
In class: Introduction of derivatives involving ln x, review of logarithm properties.
|
|
|
M 11/13/06
|
HW due: Read §3.4; write §3.3 #14 (using QR, including
simplification), 16, 19, 23, 25, 26, 35. Note:
Exercises 14, 15, and 18 were already assigned from this section. The first
time you did #14, on Oct. 11, you probably did it this way:
14. y = (x2 + 5x –
1)/x2 = 1 + 5x–1 – x–2
y¢ = 0 + (–1)5x–2
– (–2)x–3 = 2x–3 – 5x–2
When you re-do this using QR, you should get an equivalent answer. Although
simplification is usually not required, be sure to simplify your work on #14
fully so that you can verify that the answer is equivalent.
|
|
|
T 11/14/06
|
HW due: Write §3.4 #16, 17.
|
|
|
W 11/15/06
|
HW due:
1. Rewrite the formulas in the yellow boxes on pp. 135, 136, and 138 in the
more general form that we learned. The first one is done for you here as an
example. Rewrite this one and the other 5 to reinforce your knowledge. There
is not much memorization in this course, but these 6 formulas need to be
memorized for the entire year.
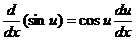
2. Write §3.5 #6, 10, 15, 21, 22.
3. Skim §3.6. You do not need to read it in the usual detail that I expect, since
I would like to teach you this material in my own way. Do, however, carefully
read Example 8 on p. 146.
|
|
|
Th 11/16/06
|
HW due: Compute the derivative of each function given.
Recopy the problem before you write the derivative. Use proper notation.
1. u(x) = sin 8x2
2. p(t) = 14 cos 9t2
3. v(x) = (cot x)15(sec
x)
4. w(x) = (sec11 2x)/(2
tan x)
5. F(t) = –csc2 2t2
+ 2 sin2 2t2
6. f (u) = cot(cot u)
7. f (x) = sin(cos(sin 3x2))
|
|
|
F 11/17/06
|
HW due: Redo yesterday’s problems as necessary, working
with other students if you wish, so that you have a completely correct set of
answers with correct notation. Then find the derivatives of the following
additional functions:
8. s(t) = tan(sin–1 t)
9. u(x) = cot2(csc2 x)
10. f (x) = (2 cot x)/(sec x – 1)
|
|
|
M 11/20/06
|
HW due: Redo #8 from yesterday, and write §3.6 #2-24 even.
A few people had correct answers for #9 and #10 from yesterday’s assignment,
but nobody came very close at all on #8.
Hint 1: Good students will not
restrict themselves to #2-24 even. Good students will do many of the
odd-numbered problems as well, in order to check the answers against those in
the back of the book.
Hint 2: For #8 from yesterday’s
assignment, the most common mistake was to treat sin–1 t as if the expression meant
“reciprocal of sin t.” Well, that’s
not what it means. (Think about it. We already have a perfectly good
function, namely csc t, that means
“reciprocal of sin t.”) In Algebra
II and again in Precalculus, you learned that sin–1 t means “the angle whose sine is t,” or in other words, the arcsin of t. The problem asks you to consider
the tangent of “the angle whose sine is t.”
The best way to handle this is to draw a picture. Show an angle whose sine is
t, and use the Pythagorean Theorem
and your knowledge of trigonometry to figure out what the tangent must be.
(It turns out to be a medium-complicated expression involving a quotient.
Therefore, the way to take the derivative is to use the Quotient Rule.)
Some portion of this assignment will be graded for accuracy, not merely the
usual completion score. If you need to work with friends, that is fine, but
make sure that you are working
together, not merely copying. Be prepared for a possible oral quiz to verify
that you know what you’re doing.
|
|
|
T 11/21/06
|
HW due: §3.6 #60. You may append this problem to your
existing HW paper if you wish. Turn in this problem, along with all of
yesterday’s assignment (including the re-do of #8 from last week) as you
arrive. We will spend the entire period viewing a video about bridges.
|
|
|
Break
|
Happy Thanksgiving. If you have a chance, please say
a prayer for my mother-in-law, Judith Mosier, who suffered a severe stroke
Nov. 19. Emergency surgery on Nov. 20 saved her life, but we do not yet know
if she is going to recover.
|
|
|
M 11/27/06
|
No additional written HW due. Please enjoy your Thanksgiving
break, and if you have any spare time, please use it to finish up any
previously assigned problems that you could not finish on the first try.
|
|
|
T 11/28/06
|
HW due: Compute the derivative of each function below. Show
your work neatly. Leave plenty of space for corrections.
1. y = cot(cot–1 3x)
2. y = cos(cot–1 3x)
3. y = cos2 (3x2 + 7 log x)
4. y = sec3 x
5. y = sec2 (sec x)
6. y = csc3 (x3)
7. y = sin(x/ex)
8. y = e2x/cot(e2 sin x)
|
|
|
W 11/29/06
|
HW due: Write up #9 and #10 below, and use your notes from
yesterday’s class to correct your problems 1-8 completely. Important: Do not erase your old
mistakes. Instead, re-do the problems in the ample margin that you allowed
yourself, and write a sentence
explaining what you did wrong the first time. (If the change is minor, use a
different color of pencil or pen to indicate the adjustment, but still write
a short sentence indicating the reason for your mistake.)
Be as detailed as you can when you explain your mistakes. For example, “Did
not understand problem” is an insufficient explanation. “Forgot QR” or
“Forgot CR” would be much better, if applicable.
As you recall, I made one boo-boo when giving the answer to #5. Here is how I
would mark up my work:
y = sec2 (sec x)
y ¢ = 2 sec(sec x)
· sec x · tan x
OOPS! Applied CR too early; forgot
that argument of sec2 () function here is sec x, not x.
Corrected version:
y ¢ = 2 sec(sec x)
· d/dx (sec(sec(x)) = 2
sec(sec x) · sec(sec(x)) · tan(sec(x)) · sec x · tan x
Please note, there were plenty of mistakes that I did not have time to mark
as I graded your papers in class. You are expected to have a completely
correct set of solutions this time around. You may consult with friends, but
the “metaknowledge” sentences describing your mistakes must be completely
your own.
Additional functions for which you should compute derivatives:
9. y = sin(cot–1 3x)
10. y = –5e2 sec x · 3e–x + 2/(ln x) +
log7 47 – log6 (x2 – 3 ln x)
|
|
|
Th 11/30/06
|
HW due: §3.6 #2-20 even, 42-48 even. Many of these problems
were previously assigned, but now you should be able to do them all
correctly. Start over from scratch,
with a fresh sheet of paper. There is no credit for recycling your earlier
paper, even if it is correct. (Of course, it is acceptable to copy from
your earlier paper if you believe it was correct.)
|
|