|
IntroCal / Mr. Hansen |
Name: _________________________ |
The IntroCal Saga: Academic Year Recap
The calculus has two main parts, differential calculus
and integral calculus. Also, at the end of the year, we spent time on four
other topics that tie the first two together: FTC, differential equations,
slope fields, and Euler’s Method. That makes a total of two major themes and
four related topics, or six big ideas. These are numbered with Roman numerals I
through VI in the presentation below.
Outline
I. The differential calculus (deals with derivatives)
A. Working def.: instantaneous rate of change
B. Alt. def.: tangential slope
C. MATH 8 to approx.
D. Formal def.: limit of difference quotient
E. Speedometer example
II. The integral calculus
A. Indefinite integrals
1. Use table or advanced
software most of the time in real life
2. Polynomials are easy, though
B. Definite integrals
1. Area under a curve
2. Riemann sums
3. Quadrature, adaptive
quadrature, MATH 9
4. Applications:
variable-factor products, accumulations of rates of change
III. FTC
A. Purpose is to link I and II
B. One version: (g
continuous and 
= g) 
C. Another version: every continuous function has an
antiderivative, namely an accumulator function
D. Summary of both versions: differentiation and integration
are inverses, since each “undoes” the other
E. Computation example: finding definite integral
without using MATH 9
F. More examples: finding antiderivative of any
continuous function, no matter how messy
IV. Diff. eqs.
A. Definition of diff. eq.
B. Determining order (first order, second order, etc.)
C. Definition of solution
D. Examples of finding solutions
V. Slope fields
A. Key idea: Lattice with stubby slope indicators
B. Useful for showing entire family of solutions at
once
C. Can be made by hand, but BIGSLOPE is faster
VI. Euler’s Method
A. Key idea: Follow straight-line paths over short
intervals to estimate the track of a diff. eq. solution
B. Usually works well if step size is small and slope
field is not chaotic
Important definition: chaos
= extreme sensitivity to initial conditions
C. Examples of using EULER program
I. The
differential calculus concerns derivatives, which are instantaneous rates
of change, sometimes called “tangential slopes.” The word “tangential” is
needed to distinguish these from average rates of change, which are “secant
slopes.” Secant slopes are easy to compute without any calculus—we just use 
, as in Algebra I and Algebra II. For derivatives, however,
we needed to learn a number of rules, such as the power rule, the product rule,
the quotient rule, the chain rule, and special rules for functions like sin x, cos x, ex, and ln x. Derivatives can be approximated with
MATH 8, whose syntax is nDeriv(function,variable,point) where “point” means the
value at which we wish to evaluate the derivative.
Example 1: If f (x) = 2x6, then 
. Therefore, 
= 12(32) = 384. Check:
nDeriv(2X^6,X,2)=384.
A derivative is defined as the limit of a difference quotient as the
step size approaches 0. That is why you are supposed to study precalculus,
which introduces the concepts of limits and difference quotients, before
studying the calculus. The idea is that if you understand limits (most people
do) and difference quotients (ditto), then you can understand limits of
difference quotients. Unfortunately, many students are unable to put the two
concepts together, even in regular calculus and HappyCal. In IntroCal, we didn’t
get too bogged down with the definition of derivative, because the definition
has very little to do with the real-world usefulness of derivatives. The main
thing is to know that the derivative represents a rate of change at some point,
and a derivative function represents a whole collection of such rates of
change. The example of a speedometer is helpful. If we glance at a speedometer,
the display shows us the derivative of our position function s at that moment. On the other hand, if
we plot the speedometer readings as a function of time, we have a graph of the
derivative function.
II. The integral calculus concerns
indefinite integrals (a.k.a. antiderivatives) and definite integrals.
Antiderivatives
are more difficult than derivatives, but our textbook contains a long table of
antiderivatives so that we don’t have to memorize all the rules. Plus, nowadays
there are many computer programs and even calculators such as the TI-92 that
will compute antiderivatives. The details are not so important. If we ever need
an antiderivative, we can use a table or some suitable software.
Antiderivatives of polynomials are easy, though, and we should remember how to
do those.
Example 2: The antiderivative of x7
– 5x5 + 3x2 – 4.2 + 
equals 
. Don’t forget “+ C”!
Definite
integrals are often defined as the area under a curve, which makes it easy
to understand why Riemann sums (sums consisting of thin rectangular areas) can
be used to approximate a definite integral. Some examples of Riemann sums are
the left endpoint rule, the right endpoint rule, the trapezoid rule, and the
midpoint rule, all of which we learned and even programmed on our calculators.
Riemann sums are a special case of a more general procedure called quadrature, which means the estimation
of an area by means of an algorithm. Simpson’s Rule is the only quadrature
algorithm we learned that is not a straightforward Riemann sum. The TI-83 and
TI-84 calculators use adaptive quadrature
for MATH 9, which means that the definite integral will be estimated by an
algorithm that varies the step size to avoid wasting processing time: large
step size in regions where the function is not changing very much, small step
size in regions where the function is changing rapidly. How does the algorithm
determine how rapidly the function is changing? By estimating the absolute
value of the derivative.
What are integrals good for? Antiderivatives are mainly
of theoretical interest, since very few real-world functions have antiderivatives
that we can find in closed form. By contrast, definite integrals are much more
practical. Although often defined in terms of “area under a curve,” the places
where definite integrals really shine are (1) computing variable-factor
products and (2) computing accumulations of rates of change (i.e., solving a
differential equation by adding up all the small bits of change indicated by
the derivative). Both of these applications are extremely important in physics,
chemistry, biology, and all types of engineering.
Example 3: Suppose that we have an object whose
density is not constant. To find the total mass of the object (which is a
variable-factor product involving density and little bits of volume), we simply
integrate the density function with respect to volume.
Example 4: Suppose that we have a furnace that
is burning natural gas at varying rates depending on the difference between the
outside and inside temperatures, both of which fluctuate over time according to
periodic functions. To find the total fuel consumption (which is a
variable-factor product involving temperature difference, fuel consumption rate
per degree of difference, and little bits of time), we simply integrate the
total consumption rate with respect to t.
Example 5: What if, in Example 4, the heating
system runs on electricity instead of natural gas, and the price of electricity
varies depending on the time of day? (Power companies sometimes do this, since
by charging more during peak usage, they can encourage people to shift some
energy consumption to off-peak times. By smoothing the demand somewhat, there
is less need to build additional power plants, and that saves money, reduces
pollution, and disrupts neighborhoods less.) We can compute the total heating
expense by throwing yet another variable-factor function, namely the price
function P(t), into the integrand.
Example 6: If we know the velocity of a race car
or other object as a function of time t,
we can compute the distance traveled by adding up all the little bits of
change. In other words, we integrate the velocity function with respect to t. Of course, if we wanted to know our
ending position, we would also need to know an initial condition (usually stated as the starting position) so that
the “+ C” ambiguity can be resolved
when we solve the differential equation ds/dt = v(t).
III. The FTC (Fundamental Theorem of Calculus) is the bridge between
derivatives and integrals. One version of FTC says that a definite integral
from a to b of any continuous function g
can be computed as G(b) – G(a), where G denotes any antiderivative of g.
This is an interesting theoretical result for people like Mr. Hansen, but it is
virtually useless in the real world, since the vast majority of functions that
we care about do not have a closed-form antiderivative. In other words, we can
talk about G, and we can even prove
that G exists, but usually we cannot
write G in a simple form that
students are happy with. Students are always looking for easy answers like “sin
x + 2” or “3 ln x – 7” (which is understandable), but G usually cannot be written out in a simple form like that.
On those rare occasions when G has a
simple form, students can find 
by using FTC. However,
we should not think that this is the central point of the course. In a bygone
era, it is true that students spent huge amounts of time computing definite
integrals by FTC, but nowadays, it is usually smarter to use MATH 9.
Nevertheless, we should be able to do a simple example by hand.
Example 7: Without using a calculator, compute 
Solution: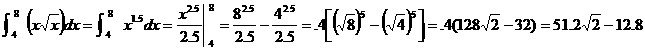 
Check: Use MATH 9 to get fnInt(X
(X),X,4,8) 
59.608. That matches
the non-calculator answer above.
Note that this was a phony “textbook” example in which the antiderivative G was easy to find. Usually, it is not
so easy. How do we find G in more
typical situations? Good question! That is where the other version of FTC comes
in. The other version of FTC says that every continuous function g has an antiderivative. If g is continuous on some closed interval D, if k is a constant, and if k
and x are both within D, then G is an antiderivative of g,
where
Note that the names FTC1 and FTC2 are not standardized between textbooks. What
the IntroCal text calls FTC1 is called FTC2 by the HappyCal text, and vice
versa. At any rate, FTC1 (IntroCal) or FTC2 (HappyCal) is often written as
which is certainly true, but that equation obscures the central idea of the
theorem, namely that every continuous function g has an antiderivative. The function G, defined as shown with the variable x as the upper limit of integration, is sometimes called an
“accumulator function” since it accumulates the rates of change represented by g. Therefore, FTC may also be summarized
as follows:
- The derivative of an accumulator function equals
the integrand.
- Differentiation and integration are inverse
operations in the sense that each “undoes” the other.
Example 8: Write a function F whose derivative is ln(sin x2 + e7x + 5) if it
is known that F(2) = 11.3.
Solution: What a mess! Obviously there is no hope of finding an
antiderivative in any table. However, by FTC, we know that
is an antiderivative of the messy function given. Moreover, G(2) = 0 since the integral from 2 to 2
of anything is 0. Therefore,
solves the problem nicely. With a little practice, one can do problems like
this very quickly, and if there is a need to know the value of F(x)
for some specific x value, MATH 9
will answer the question.
Example 9: Write a function L
whose derivative is cos(cos(x + ln (3
+ x444))) if it is known
that L(0.98) = –311.217, and compute L(0.99).
Solution: 
, and L(0.99) –311.2082 by calc. No
work needed!
IV. Differential equations (diff. eqs.)
are equations that contain at least one derivative. If the highest derivative
present is a first derivative, we have a first-order diff. eq.; if the highest
derivative present is a second derivative, we have a second-order diff. eq.;
and so on. Diff. eqs. describe the nature of magnetism and electrical currents,
the forces affecting the motions of the planets, the effects of gravity,
radioactive decay, and vast numbers of other physical processes. If you want to
do anything at all at the college level in science or engineering, you need to
be acquainted with diff. eqs. to some degree.
The most basic thing to know about diff. eqs. is the meaning of the word
“solution.” After all, if you plug a diff. eq. into a software package to
generate a solution, but you don’t know what the word “solution” means in this
context, you really have not accomplished anything.
In lower math courses, the word “solution” means a number, or sometimes a set
of numbers, that can satisfy some equation or inequality containing an unknown
variable. For example, the solution to x
+ 3 = 5 is {2}, and the solution to x2
< 9 is {x: –3 < x < 3}. By the time you get to
Algebra II, you (hopefully) understand that a solution can also be a set of
ordered pairs (or ordered triples, or ordered n-tuples, or whatever)
satisfying a system of equations and/or inequalities.
In diff. eqs., the word “solution” means something entirely different. It is a function or relation that fulfills the
initial conditions (if any) and such that when you take the derivative and plug
that simplified expression for the derivative into the diff. eq., the equation
balances. We call this “satisfying the equation.” An initial condition is a point (usually an ordered pair) through
which the solution curve is required to pass.
Example 10: Solve the diff. eq. dy/dx = x/2
with initial condition (3, –7).
Solution: You may be able to write a general solution by inspection: y = x2/4
+ C. We call this a general solution
because the value of C is still
unknown. If you were not able to do this by inspection, then multiply both
sides by dx to get dy = (x/2) dx. Then antidifferentiate
both sides and consolidate the constants of integration into a single C on the
right:
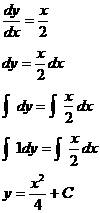
The answer above for y is called a general solution. Now, to find C, we must plug in 3 for x and –7 for y as follows:
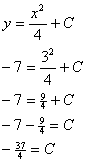
Particular solution: 
. Note that the “y
=” must be written, since otherwise we don’t have a function.
Example 11: Solve the diff. eq. dy/dx = xy/2
with initial condition (3, –7).
Solution: This is somewhat harder. Since there is some y mixed into the derivative, we cannot
simply write down an antiderivative. Multiply both sides of the equation by dx and divide both sides by y, and then proceed as follows:
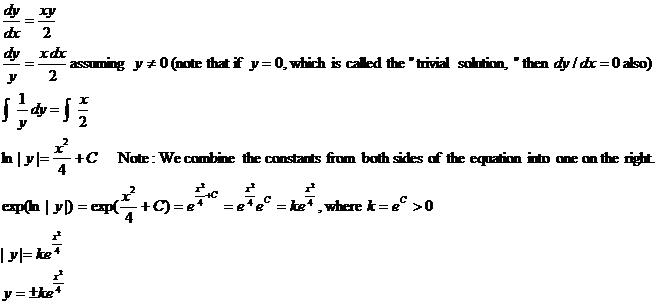
We have solved for y, but since k is unknown, all we have so far is a
general solution. The general solution, y
= ±k exp(x2/4), can be simplified if
we observe that the trivial solution and the “plus or minus” can all be
summarized by saying y = K exp(x2/4) where K is
some arbitrary real number. To find the value of K, we must plug in x = 3
and y = –7 as follows:
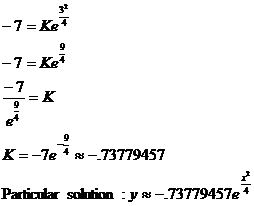
Note: Examples 10 and 11 are called separable diff. eqs. since we were able
to separate everything involving y
and dy on the left, and everything
involving x and dx on the right. Only a tiny fraction of diff. eqs. are separable.
Most of the time, we must rely on slope fields and Euler’s Method to find
solutions.
V. Slope fields are graphical
displays similar to the “wind arrow” charts sometimes seen on The Weather
Channel, except that arrowheads are not necessarily used, and usually all the
slope indicators are the same length. The key idea is to produce a lattice
(i.e., integer grid) of points with a stubby little slope indicator on each
lattice point.
The purpose of a slope field is to indicate the general “swoosh” of all the
possible solutions. In other words, you can get a sense of the entire family of
solutions at once. You can make a slope field manually, with pencil and paper,
but it is usually easier to use a computer or transcribe the plot from
BIGSLOPE.
VI. Euler’s Method is an algorithm
for estimating the solution track of a diff. eq. The key idea is to follow
straight-line paths over short intervals. As long as the step size is small and
the slope field is not chaotic (where “chaotic” means extremely sensitive to
initial conditions), the Euler estimates should be fairly close to reality. It
is possible to execute Euler’s Method with pencil and paper, but most people prefer
the EULER program (see 5/1/2007 calendar entry)
or equivalent. The algorithm is not too hard, but it is a nuisance to compute
with pencil and paper. First, we need to know an initial condition (x0, y0) and a step size, h.
Then for each additional point, one by one, we use this idea:
Since this is IntroCal, we usually let the EULER program do all the work for
us. Certainly that will be the case on the final exam.
Example 12: If dy/dx = xy/2,
subject to the initial condition (3, –7), estimate y when x = 2.5.
Solution: By executing the EULER program with x = 3, y = –7, n = 5, h = –0.1, we obtain y(2.5)
–3.2924 when we check
lists L1 and L2. Note that for most diff. eqs., EULER or
something like it will be our only choice, since the diff. eq. usually cannot
be solved precisely. However, we are very lucky with this particular example,
since we know the true particular solution, namely y » –0.73779457 exp(–x2/4).
Plugging in x = 2.5, we get y(2.5) –3.5198, which means
that the Euler estimate had a relative error of more than 6%.
What went wrong? Most likely the step size was too large. Plotting the curve
shows that the curve is very steep in a neighborhood of x = 3. If we rerun EULER with x
= 3, y = –7, n = 50, h = –0.01, we
obtain y(2.5) –3.498586, which
represents a much smaller relative error of only about 0.6%.