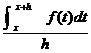Honors AP Calculus / Mr. Hansen

(8)   Name: _______________________________________

11/9/2006

Mr. Hansen’s use only (bonus point for spare batteries): _______

 

Test on §§4-7 through 5-6

Calculator is permitted throughout. Point values are shown in parentheses.

 

1.
(6 pts.)

For small values of h,  is an approximation of

(–1.5 for error)

(A) f (x)

(B) f (h)

(C) f ¢(x)

(D) f ¢(h)

(E) f ¢¢(x)

 

 

2.
(6/1.5)

Which of the following would be an adequate (or more than adequate) hypothesis to imply the MVT conclusion?

 

(A) f continuous on (a, b)

(B) f continuous on [a, b]

(C) f differentiable on (a, b)

(D) f differentiable on [a, b]

(E) f continuous and differentiable on (a, b)

 

 

3.
(4+8)

A curve is defined by 2x2 – 3y2 + xy = 3xy2.

(a)

Prove that the curve passes through (–1, 2).

 

 

 

 

(b)

Compute the slope of the tangent at (–1, 2).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4.(a)(6)

State FTC1.

 

 

 

 

(b)
(8)

Let g(x) be continuous on Â. Use FTC1 to prove that , where c is a constant.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(c)(4)

What do we call the result in (b), approximately?

 

5.
(6+6)

Let x = 3 cos t, y = 4 sin t, 0 £ t < 2p.

(a)

Sketch the set of points traced.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(b)

Compute the tangent slope at any point you wish, provided the tangent is neither vertical nor horizontal. Do not use decimal approximations.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6.
(8)

Compute  precisely (no approximations), showing your work.

 

7.
(6)

Compute  if f is continuous on Â+.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8.
(8)

Use the linear approximation of y = cos 2x near the point where x = p/3
in order to estimate y when x = p/3 + 0.004. Show all work.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

9.(a)(6)

State MVT in its usual form.

 

 

(b)
(6)

Find a point in (2, 3) where the MVT conclusion is true for the function y = sin 5x
with respect to [2, 3]. No work is required.

 

 

 

 

 

 

 

 

(c)
(4)

How many solutions to part (b) are possible? No work is required.