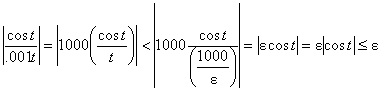Honors AP Calculus / Mr. Hansen	Name: ______________KEY_____________________
10/12/2006	Mr. Hansen’s use only (bonus point for spare batteries): _______

Test on Chapters 2 and 3

1.	C
2.	E (General antiderivative is x^3 − 3.5x^2 + C, and the one which makes f (1) = 2 is f (x) = x^3 − 3.5x^2 + 4.5. Then plug in to get the answer.)
3.	D (The expression in parentheses is a constant.)
4.	D (Use a difference quotient.)
5.	A (Generalize result from #4, then perform algebra. Students seem to find this problem to be either easy or extremely difficult.)
6.	B by definition of derivative (limit of difference quotient)
7.	B
8.	C (intersections give delta of .003741019 on the left, .0037270759 on the right; always remember to round down)
9.	C (can get by process of elimination) A is not possible since N(2) = 0 by inspection, and N(4) = 110/3 (given). B is acceptable (and in fact I allowed it for credit) but is not the best answer. See #10 for a hint. D makes no sense. E is enticing, except that any antiderivative of t^2 + 3t is of the form which is a function of t, not a function of x.
10.	A
11.	The proposed definition is acceptable. (Remember that the secants must be able to stretch either to the left or to the right. Otherwise we would have only a one-sided derivative.) The derivative value, , can also be thought of as the slope (iff such slope exists and is uniquely defined) of a tangent to the curve at (c, g(c)), or as the instantaneous rate of change of the function g at the point x = c. However, these “ways of thinking” of are not fully rigorous. You could also give either or both of the two standard (fully rigorous) definitions using difference quotients:
12.	iff (or “if and only if”)
	<
13.	Since infinity is not a number, it is nonsense to speak of “approaching infinity.” Strictly speaking, the notation should be replaced by the words “as x increases without bound.”
14.	(a) Graph should resemble a sinusoid, except with a vertical asymptote at t = 0 and decreasing amplitude as t increases. The centerline should be shown to be above the t axis (ideally at D = 4), but no detail was required. Any vaguely sinusoidal squiggle with decreasing amplitude and centerline above 0 will qualify.
	(b) 4 (since second term vanishes as t grows without bound)
	(c) If M = 10,000, then t > M implies that the second term is which is bounded by 0.1 in absolute value since the cosine of any value has range [−1, 1]. The presence of a strict inequality earlier in the chain makes the final inequality strict; i.e., the second term is strictly bounded by the open interval (−.1, .1).
	D(t) is differentiable on the positive reals, hence certainly continuous for all values of t > 10,000. Therefore, as long as t > 10,000, the sum of 4 and the second term is strictly bounded by the interval (3.9, 4.1). (Q.E.D.)
	(d) You can always use for this function. Proof (optional) is as follows: If t > , then the second term’s absolute value is . (Q.E.D.)
15.
16.
17.