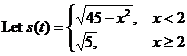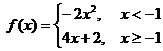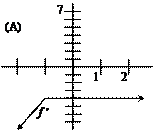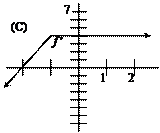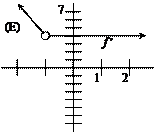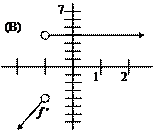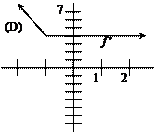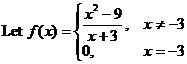Honors AP Calculus / Mr. Hansen

Name: _______________________________________

9/18/2006

Mr. Hansen’s use only (bonus point for spare batteries): _______

 

Test on Chapter 1 and Class Discussion

Please read: Calculator is OK throughout. Problems #1, #2, and #25 are 6 points each; all others except #19 are 4 points each. Important: For multiple-choice questions (#3-24), mark answers only on the bubble sheet, not here. Multiple-choice scoring is as follows: 4 points if answer is correct, 0 points if blank, –1 point if wrong.

 

1.
(6)

Let v(t) be a continuous velocity function, and let h(t) denote the height of a particle at time t. If h(3) is given to be 3.6 m above ground, find h(4). Hint: Use FTC1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.
(6)

State FTC1 and FTC2. Labeling does not matter, since textbooks differ on which is called which.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.

Which of the following is an example of a calculus?

 

 

(A) statistics
(B) politics
(C) history

(D) navigation
(E) biology

 

 

 

 

4.

Categorize the following: .

 

 

(A) first-order ODE
(B) second-order ODE
(C) first-order PDE

(D) second-order PDE
(E) cubic polynomial equation

 

 

 

 

5.

A function f for which the function f ¢ can be found for each point in Df is said to be . . .

 

 

(A) in closed form
(B) an initial condition
(C) a differential equation (“diffeq.”)

(D) derivitable
(E) differentiable

 

 

 

 

6.

The trapezoid rule approximation for , using 4 subintervals (i.e., 5 mesh points), is . . .

 

 

(A) 77.492
(B) 77.493
(C) 77.557

(D) 77.558
(E) 78.000

 

 

 

 

7.

The correct answer to #6 is . . .
(A) somewhat lower than the true integral, since the integrand is an upward-concave function
(B) somewhat higher than the true integral, since the integrand is an upward-concave function
(C) somewhat lower than the true integral, since the integrand is a downward-concave function
(D) somewhat higher than the true integral, since the integrand is a downward-concave function
(E) a correct approximation of the true integral, since the integrand is quadratic

 

 

 

 

8.

An accumulator function is . . .

 

 

(A) any linear function
(B) a definite integral with constant endpoints
(C) a definite integral with a variable upper endpoint
(D) any indefinite integral
(E) an indefinite integral, but only if the integrand is linear

 

 

 

 

9.

An initial condition for a differential equation is a “clue” consisting of . . .

 

 

(A) an ordered pair (often) that allows us to select a particular solution from among all possible general solutions
(B) an ordered pair (often) that allows us to write the general solution in closed form
(C) a number or set of numbers that allows us to select a particular solution from among all possible general solutions
(D) a general equation
(E) a general equation and one or more derivatives that are satisfied

 

 

 

 

 

In problems 10 through 12, the functions s(t), v(t), and a(t) are to be interpreted as position, velocity, and acceleration at time t, respectively.

 

 

 

 

10.

  . The average velocity from t = 0 to t = 4 is . . .

 

 

(A) 0
(B) –1.118
(C) –2.236

(D) 4.422
(E) –4.422

 

 

 

 

11.

If s(t) is defined as in #10, then v(3) is . . .

 

 

(A) 0
(B) 2.236
(C) –2.236

(D) 2.449
(E) DNE

 

 

 

 

12.

For any particle, not necessarily the particle whose position was defined in #10, the expression , where a(t) is continuous, equals . . .

 

 

(A) change in position (i.e., Ds) from t = 0 to t = 4
(B) change in velocity (i.e., Dv) from t = 0 to t = 4
(C) change in acceleration (i.e., Da) from t = 0 to t = 4

(D) v(4)
(E) s(4)

 

 

 

 

13.

If f (x) = |x|, then f ¢(0) is . . .

 

 

(A) 0
(B) 1
(C) –1

(D) ±1
(E) DNE

 

 

 

 

14.

For a continuous function y = f (x), a cusp is a point (x, y) such that . . .

 

 

(A) f ¢ is a continuous function on Df
(B) f ¢ has vertical asymptote at x
(C) f ¢(x) does not exist

(D) f has a vertical asymptote at x
(E) f has a step discontinuity at x

 

 

 

 

15.

Given: . This is a separable diffeq. If nothing more is given, then we could use techniques later in our course to find . . .

 

 

(A) a general solution
(B) a particular solution
(C) an initial condition

(D) a value for y and a value for y¢ corresponding to any desired value of x Î Df

(E) both (B) and (D)

 

 

 

 

16.

Any continuous function f has . . .

 

 

(A) a unique antiderivative
(B) a family of antiderivatives
(C) a derivative (f ¢)

(D) both (A) and (C)
(E) both (B) and (C)

 

 

 

 

17.

For which function f do both f ¢ and f ¢¢ appear to be positive on all of Â?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

18.

For the function G(x) = sin2 x + 3 cos2 x, the instantaneous rate of change when x = –1 is . . .

 

 

(A) 1.818
(B) –1.818
(C) 1.819

(D) –1.819
(E) 0

 

 

 

 

19.

On the AP exam, there are 4 graphing calculator features that you may use without having to show work, in addition to the obvious operations of arithmetic and function evaluation. They are . . .

 

(2 pts., no penalty for guess)

(A) MATH 8, MATH 9, MATH 0, and anything on the 2nd CALC menu
(B) MATH 8, MATH 9, MATH 0, and finding a max. or min. (2nd CALC 4 or 5)
(C) MATH 8, MATH 9, MATH 0, and the intersection of 2 functions (2nd CALC 6)
(D) MATH 8, MATH 9, MATH 0, and a sketch of a graph
(E) MATH 8 (or 2nd CALC 6), MATH 9 (or 2nd CALC 7), MATH 0 (or 2nd CALC 2 or 5), and extremum finding (2nd CALC 4 or 5)

 

 

 

 

20.

Are both x3 and x3 + 1 valid antiderivative functions for the function y = 3x2?

 

 

(A) No, because the first one is lacking a constant term.
(B) No, because the derivative of the first one is not 3x2.
(C) No, because the derivative of the second one is not 3x2.
(D) Yes, because the general antiderivative of y is x3 + C, and both given functions are of that form.
(E) Yes, because any two antiderivatives must differ by 1.

 

 

 

 

21.

Let a function be defined piecewise as
Which graph correctly illustrates f ¢?

 

 

 

 

 

 

 

 

 

 

 

 

 

22.

Recall that the notation x ® –3– means “as x approaches –3 from below” (i.e., from the left).
 . Therefore,  is . . .

 

 

(A) 0
(B) –3
(C) –6

(D) –9
(E) DNE

 

 

 

 

23.

For the function defined in #22,  is . . .

 

 

(A) 0
(B) –3
(C) –6

(D) –9
(E) DNE

 

 

 

 

24.

The function defined in #22 has . . .

 

 

(A) a vertical asymptote at x = –3
(B) a step discontinuity at x = –3

(C) no discontinuity anywhere (i.e., f is continuous on Â)
(D) a graph whose shape is parabolic
(E) a graph whose shape is parabolic, with the exception of x = –3

 

 

 

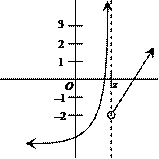
25.
(6 pts.)

For the function f sketched at left, write the limit of f (x) as x approaches z from below, from above, and as a 2-sided limit. Write 3 equations or statements using proper “lim” notation. Your notation will be graded as well as your answers.

From below (equation): _____________________________

From above (equation): _____________________________

2-sided limit (equation): _____________________________

 

 

 

BONUS SECTION (½ pt. each)
Mark answers for B1-B4 on your bubble sheet, not here.
There is no penalty for wrong guesses in this section.

 

 

B1.

Choose an answer, A through E. Hint: Choice D is not correct.

 

(A)
(B)
(C)
(D)
(E)

 

 

B2.

What is the only movie that Mr. Hansen has seen in a theater during calendar year 2006? Hint: Choice D is not correct.

 

(A) An Inconvenient Truth
(B) The Lake House
(C) World Trade Center
(D) Cars
(E) The Devil Wears Prada

 

 

B3.

Choose an answer, A through E. Hint: Choice D is not correct.

 

(A)
(B)
(C)
(D)
(E)

 

 

B4.

Which of the following sentences is correct in grammar and punctuation? Hint: Choice D is not correct.

 

(A) The problem is that nobody has responded yet.
(B) The problem is, that nobody has responded yet.
(C) The problem is is that nobody has responded yet.
(D) The problem, is is that nobody has responded yet.
(E) The problem is, is that nobody has responded yet.

 

 

B5.

What 2-letter word do we try never to use in the calculus? _______ Hint: The word does not appear anywhere in today’s test.