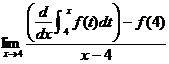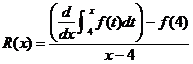Honors AP Calculus / Mr. Hansen	Name: _______________________________________
1/5/2007

OCQ (Oral Cumulative Quiz)

Ground rules:

• There will be one student “on deck” outside the piano room while each student is being quizzed. All other students must remain in Room 202 with the door closed.
• The student who is “on deck” may not communicate with the students in Room 202, not even by whispering. The hallway must be kept quiet, and the door to 202 must be closed.
• Arguing and sharing ideas with other students in 202 are encouraged.
• There are no restrictions on information sharing (even intelligence sharing from previously summoned students), nor are there any restrictions on note-taking. However, the less you need to refer to notes, the more successful your quiz will be judged to be.
• You may be summoned into the piano room more than once, either as a result of random selection or as a way to have another chance to earn an A.
• People who are randomly selected near the beginning may receive a few hints or “leading questions” during their quiz, since they had less time to prepare.
• Error-carried-forward” (ECF) is permitted. For example, if you cannot find the answer to part (a), you could say, “I will use the name A to stand for the answer to part (a),” and then you could continue.
• You may request clarification of the questions during your oral quiz. However, try to ask good questions, avoiding asking about things that have already been defined.

1.	Let an acceleration function a(t) be a continuous function of time t, where t is measured in seconds. If the velocity at time 3 satisfies the equation v(3) = 2.6 m/sec, explain how you would go about finding (a) v(5) (b) the average velocity over the interval 3 £ t £ 7.5.
2.	Let the givens be as in problem #1, but this time suppose that your goal is to find s(4), the position at time t = 4. You may request any single numeric value from me that you wish, other than s(4) itself, in order to help you attain your goal. For example, you could request v(3), but that would be silly, since v(3) was already given to be 2.6. (a) What would you request? Be specific. There is no single right answer to this question. (b) What are the units of the value you requested in #2(a)? (c) Explain how you might employ the value in #2(a) to find s(4).
3.	In this question, the phrase “accumulator function” refers to a certain type of function we studied. (Fill in the blanks.) (a) Specifically, an accumulator function is a function defined as a(n) ______ ______ of a(n) ______ function f. The lower endpoint is a(n) ______ , and the upper endpoint is a(n) ______ . (b) Every accumulator function of this type is a(n) _________________ of its integrand. (c) Let f be continuous on Â. If it is given that the limit exists, simplify , explaining exactly what you are doing at every step and what the final answer represents. (d) Let , which is the same expression except without the limit. Compute R(4.001) if it is also given that f ¢(4.001) = 2 and f is linear on [3, 5].
4.	Let P1 and P2 be two curved paths in the xy-plane. You can think of these as parametric functions of time t. It is also given that are continuous for each path, and there is no value t for which both derivatives are simultaneously 0. Reminder: means dx/dt, and means dy/dt. (a) What type of object is P1(t)? A number, a set, or something else? (b) Suppose that "t, P1(t) and P2(t) are symmetric with respect to the line y = x. At time t0, what relationship exists, if any, between the line tangent to path P1 and the line normal to path P2?