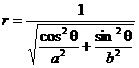|
Th 3/1/07
|
Test on Chapter 9. There will also be one question on arc length and
one question on volume (either plane slicing or a solid of revolution). You
need to memorize the green boxes on pp. 418, 420, 437, 443, 447, 452, 469,
473, and 486, as well as the arcsine and arctangent derivatives on p. 470 and
the various arc-length and volume formulas provided in class. Any other green
box contents, if required on the test, will be provided for you.
Important:
Bring your HW binder to class so that your recent HW can be scanned while you
are taking the test.
|
|
|
F 3/2/07
|
In class: Tenth dimension video.
HW due: §10-2 #6, 12, 13; §10-3 #2, 3, 13.
Optional: Re-do yesterday’s test in its entirety. An adjustment
will be made to your test score if you demonstrate conclusively that you
really knew the material but were simply pinched for time. Yes, if you desire
this bonus, you really do need to do the entire test, not simply the problems
you know you got wrong. (The reason is that for any problems that you get
wrong twice, I can see how much metaknowledge you had, or more correctly, did
not have. If you get them right on the second try, I can see how capable you
are of learning from your mistakes.)
Note: I will accept the test
revisions until 4:00 p.m. today (Friday), in case that helps you. You may
work with friends to share ideas, but the writing that you do must be your
own. No copying is allowed.
|
|
|
M 3/5/07
|
HW due: Read the related rates tutorial and practice
problems. Do a few of the practice problems on paper (enough to get the
general feel), and then write §10-4 #5, 9, 14. The steps are always the same:
1. Write an equation that relates the quantities of interest. Frequently this
is the Pythagorean Theorem, a volume formula from geometry class, or
something of that sort.
2. Differentiate implicitly.
3. Plug in the known quantities and attempt to solve for the unknown.
|
|
|
T 3/6/07
|
Oops! No additional HW since it was not posted in
time. Please use the time to study for Thursday’s quest and/or work on the
extra credit problem given during class.
Extra credit problem: Use the correct hint from last week’s test
problem #1(c), namely that the ellipse has polar form 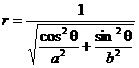 , to prove that the polar area is  .
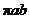The polar form I sold you last week is no good—a peanut instead of an
ellipse. For values of a and b that are roughly the same size, the
difference between the two polar equations is almost unnoticeable, but for an
ellipse with high eccentricity, the difference is huge.
You will also need a table of integrals in order to apply FTC. Big hint: Look for an antiderivative
of the form  ,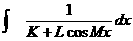
and then apply some tricky algebra to convert your integrand to that form.
You can ask the IntroCal students to show you a table of integrals in the
back of their textbook, or you can find one on the Web. After you conquer
that hurdle, there is another significant hurdle that presents itself at the
end, and the hints I offer are (1) take advantage of ellipse symmetry and (2)
remember §9-10.
Because there is so much to do here, even with the hints, I will offer
“immunity” on Thursday’s upcoming quest to anyone who submits an original
solution. If you submit a group solution, partial immunity will be offered.
This is like Survivor on TV: You
can’t get voted off the island (or fail the quest) if you have immunity. If
you don’t need the immunity, you can have up to 15 bonus points instead,
prorated for group projects. For example, a group of 3 could earn 5 points
each. (And frankly, with 3 brains working on this problem, you could probably
finish it off in an hour or so.) Going solo is also possible for some of you.
Good luck!
|
|
|
W 3/7/07
|
HW due: §10-5 #1-4 all, §10-6 #6, 10. There is no new
material here, simply some applications of things we have already learned.
These problems serve as good review problems.
|
|
|
Th 3/8/07
|
Quest (70 pts.) on §9-10 and §§10-1 through 10-6. Problems will be drawn from related rates problems,
optimization problems, improper integrals, motion problems, average value
problems, and maybe even some problems like those from yesterday that combine
several topics.
|
|
|
F 3/9/07
|
Last day of quarter. No additional HW is officially
due today, but I would like you to read §10-7.
Yesterday’s quest will be scored
holistically and can be enhanced if you submit corrections. If you wish to prepare
corrections, then please submit them before I leave at 3:30 p.m. today, along
with a signed statement certifying that your work is your own. I have to
compute quarter averages over the weekend. If you had one or more problems
you could not complete during the quest, please realize
(1) that strategy will not work very well during the AP exam (you need to
work faster), and
(2) you really need to do those problem(s).
Some points to ponder regarding the problems . . .
1. MATH 9 can almost be used as a
check here, although it violates the published accuracy tolerance.
2. For full credit, you need units that indicate a rate of some sort.
3. Nobody had a reasonable answer to the bonus. (Several answers were in
dollars, which would have been OK, except that everyone who submitted an
answer, whether in dollars or in British pounds, was way off. Most of the
answers to the main question were acceptable, but the bonus does not refer to
the main question.)
4. Several students, who perhaps absentmindedly integrated the wrong
function, gave answers that were completely unreasonable. Please think about
your answers if the rest of the units are in the realm of possibility!
5. Several students used lateral surface area instead of total surface area.
Of course, this changes the answer completely. Not that I would ever want to
compare you with another class, but the IntroCal students faced a very
similar problem on their recent quest, and most of them were able to solve
it.
|
|
|
M 3/12/07
|
HW due: Read §10-7; write §10-7 #2. You may omit part (d)
for now if you wish, because we have not yet discussed the technique.
Everything else is straightforward. Reminder:
Use angle bracket notation—e.g., 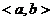 —when writing vectors in component form, and use the format
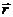 (or, if you are
lazy, 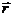 ) when denoting vectors by a single letter. Since the unit
vectors can be written as  , every vector in Â2 can be
written (if you wish or need to) as  .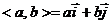
|
|
|
T 3/13/07
|
HW due: Read §11-2 (especially Example 2); write §10-7 #2d,
4, 7, 9, 14, 15.
|
|
|
W 3/14/07
|
HW due: Read §11-3; write §11-2 #6, 7, 8.
|
|
|
Th 3/15/07
|
HW due: Read §11-6; write §11-3 #1, 5, 6, 9, 11, 12. Because
this is a difficult history week, you may omit any two problems without
penalty, as long as you do at least one of the last two.
Note: For spherical shells (e.g.,
#11c and #12), dV would logically
have to be the volume of a spherical shell of infinitesimal thickness. Just
as we found the volume of a disk of thickness dx to be pr2dx, or the
volume of a cylindrical shell of thickness dr to be 2prh dr, we can find the volume of spherical shell. What is
the common thread? With both disks and shells, we are taking the exposed surface area of the very thin
component and multiplying by dx or dr to get dV. With spherical shells, you follow the same guidance. Send me
an e-mail if you have trouble figuring out how to set up dV for spherical shells. (You need the formula for surface area
of a sphere. If you have forgotten the formula from geometry class, you can
look it up.)
Additional note for #11ab: Distance
of a point from a plane was defined in geometry class, as was distance of a
point from a line. If you include these distances on your sketch (as you
should), you will see that they are straightforward to calculate.
|
|
|
F 3/16/07
|
HW due: §11-6 #3, 8, 12. Since you already have experience working
with variable-factor products, these should go fairly quickly. With any
additional time, work on patching up loose ends from yesterday’s problem set.
|
|
|
Spring Break
|
Please relax, but note that there are 7 review
problems and a book due when you return. Also, you will make me very happy if
you work one or two problems each day from your AP review book. Please keep a
written log of your work, and show your scratch work in your binder. Label
each problem that you do with page
number and problem number.
Most of the AP review books provide complete solutions and explanations to
help you learn from your mistakes.
Choose problems randomly or, if you prefer, by selecting problems that look
interesting and challenging. The only problems you need to avoid are those
involving power series. (If you read ahead in the textbook, you can even do
those.)
Five minutes per day will pay big dividends later. If you can’t do five
minutes a day, then try 10 minutes every other day. Seriously!
Some bonus points will be provided to people who do a good job with their
written AP log. For everyone else, I wish you a happy spring break, but
remember that there are 7 review problems and a book purchase that are
required of everyone (see 4/2 calendar entry).
|
|